OpenGL - координаты мыши в координатах пространства

Моя цель - поместить сферу прямо туда, куда указывает мышь (с координатой Z, равной 0).

Я видел этот вопрос, но я еще не понимал концепцию матриц MVP, поэтому я немного исследовал, и теперь у меня есть два вопроса:

Как создать матрицу вида из настроек камеры, таких как lookup, eye и up vector?

Я также прочитал этот урок о нескольких типах камер и этот для webgl.

Я все еще могу собрать все воедино, я не знаю, как получить матрицу проекции также...

Какие шаги я должен сделать, чтобы реализовать все это?

Источник

1 ответ

Решение

При рендеринге каждая сетка сцены обычно преобразуется матрицей модели, матрицей вида и матрицей проекции.

  • Матрица проекции:
    Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Матрица проекции преобразуется из пространства просмотра в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) в диапазоне (-1, -1, -1) в (1, 1, 1) путем деления с компонентом w координат клипа.

  • Посмотреть матрицу:
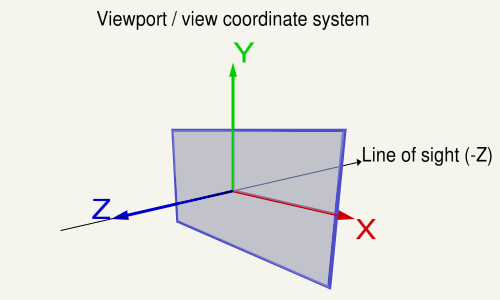
    Матрица вида описывает направление и позицию, с которой просматривается сцена. Матрица вида трансформируется из мирового пространства в пространство зрения (глаза). В системе координат в области просмотра, ось X указывает влево, ось Y вверх и ось Z вне вида (Обратите внимание, что в правой системе Z-ось является перекрестным произведением X- Ось и ось Y).

  • Модельная матрица:
    Матрица модели определяет местоположение, ориентацию и относительный размер сетки в сцене. Матрица модели преобразует позиции вершин из сетки в мировое пространство.

Модель матрицы выглядит следующим образом:

( X-axis.x, X-axis.y, X-axis.z, 0 )
( Y-axis.x, Y-axis.y, Y-axis.z, 0 )
( Z-axis.x, Z-axis.y, Z-axis.z, 0 )
( trans.x,  trans.y,  trans.z,  1 )


Посмотреть

В области просмотра ось X направлена ​​влево, ось Y вверх и ось Z вне вида (обратите внимание, что в правой системе ось Z является перекрестным произведением оси X и оси Y). Ось).

просмотреть координаты

Код ниже определяет матрицу, которая точно инкапсулирует шаги, необходимые для вычисления взгляда на сцену:

  • Преобразование координат модели в координаты области просмотра.
  • Вращение, чтобы смотреть в направлении взгляда.
  • Движение в положение глаз

Следующий код делает то же самое, что и gluLookAt или же glm::lookAt делает:

using TVec3  = std::array< float, 3 >;
using TVec4  = std::array< float, 4 >;
using TMat44 = std::array< TVec4, 4 >;

TVec3 Cross( TVec3 a, TVec3 b ) { return { a[1] * b[2] - a[2] * b[1], a[2] * b[0] - a[0] * b[2], a[0] * b[1] - a[1] * b[0] }; }
float Dot( TVec3 a, TVec3 b ) { return a[0]*b[0] + a[1]*b[1] + a[2]*b[2]; }
void Normalize( TVec3 & v )
{
    float len = sqrt( v[0] * v[0] + v[1] * v[1] + v[2] * v[2] );
    v[0] /= len; v[1] /= len; v[2] /= len;
}

TMat44 Camera::LookAt( const TVec3 &pos, const TVec3 &target, const TVec3 &up )
{ 
    TVec3 mz = { pos[0] - target[0], pos[1] - target[1], pos[2] - target[2] };
    Normalize( mz );
    TVec3 my = { up[0], up[1], up[2] };
    TVec3 mx = Cross( my, mz );
    Normalize( mx );
    my = Cross( mz, mx );

    TMat44 v{
        TVec4{ mx[0], my[0], mz[0], 0.0f },
        TVec4{ mx[1], my[1], mz[1], 0.0f },
        TVec4{ mx[2], my[2], mz[2], 0.0f },
        TVec4{ Dot(mx, pos), Dot(my, pos), -Dot(mz, pos), 1.0f }
    };

    return v;
}


проекция

Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Он преобразуется из пространства глаза в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) путем деления на w компонент координат клипа. НДЦ находятся в диапазоне (-1, -1, -1) - (1,1,1).
Каждая геометрия, которая находится вне НДЦ, обрезается.

Объекты между ближней и дальней плоскостями усеченной камеры отображаются в диапазон (-1, 1) НЦД.


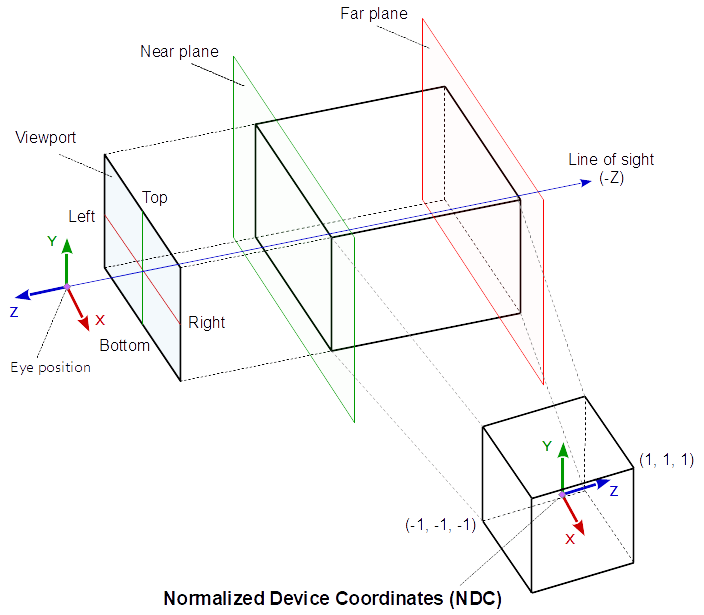
Ортографическая проекция

В ортогональной проекции координаты в глазном пространстве линейно отображаются на нормализованные координаты устройства.

Ортографическая проекция

Ортографическая матрица проекции:

r = right, l = left, b = bottom, t = top, n = near, f = far 

2/(r-l)         0               0               0
0               2/(t-b)         0               0
0               0               -2/(f-n)        0
-(r+l)/(r-l)    -(t+b)/(t-b)    -(f+n)/(f-n)    1


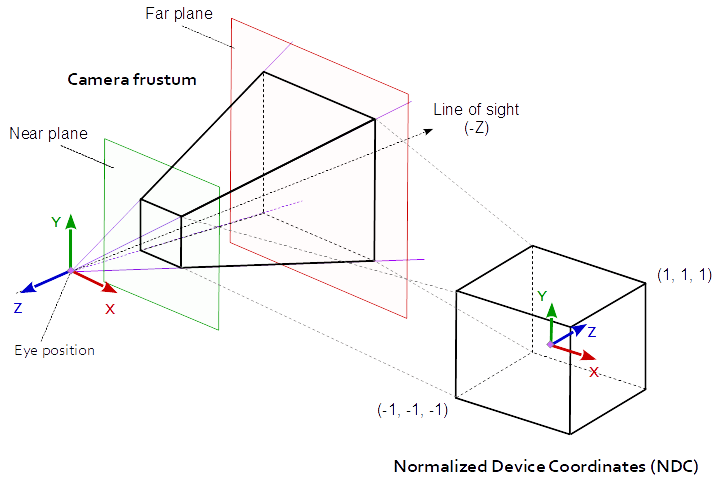
Перспективная проекция

В перспективной проекции матрица проекции описывает отображение из трехмерных точек в мире, как они видны с камеры-обскуры, в двумерные точки видового экрана.
Координаты пространства глаза в усеченной области камеры (усеченная пирамида) отображаются в куб (нормализованные координаты устройства).

Перспективная проекция

Матрица перспективной проекции:

r = right, l = left, b = bottom, t = top, n = near, f = far

2*n/(r-l)      0              0                0
0              2*n/(t-b)      0                0
(r+l)/(r-l)    (t+b)/(t-b)    -(f+n)/(f-n)    -1    
0              0              -2*f*n/(f-n)     0

где:

a = w / h
ta = tan( fov_y / 2 );

2 * n / (r-l) = 1 / (ta * a)
2 * n / (t-b) = 1 / ta

Если проекция симметрична, когда линия визирования находится в центре порта обзора, а поле обзора не смещено, матрицу можно упростить:

1/(ta*a)  0     0              0
0         1/ta  0              0
0         0    -(f+n)/(f-n)   -1    
0         0    -2*f*n/(f-n)    0


Следующая функция рассчитает ту же матрицу проекции, что и gluPerspective делает:

#include <array>

const float cPI = 3.14159265f;
float ToRad( float deg ) { return deg * cPI / 180.0f; }

using TVec4  = std::array< float, 4 >;
using TMat44 = std::array< TVec4, 4 >;

TMat44 Perspective( float fov_y, float aspect )
{
    float fn = far + near
    float f_n = far - near;
    float r = aspect;
    float t = 1.0f / tan( ToRad( fov_y ) / 2.0f );

    return TMat44{ 
        TVec4{ t / r, 0.0f,  0.0f,                 0.0f },
        TVec4{ 0.0f,  t,     0.0f,                 0.0f },
        TVec4{ 0.0f,  0.0f, -fn / f_n,            -1.0f },
        TVec4{ 0.0f,  0.0f, -2.0f*far*near / f_n,  0.0f }
    };
}


3 решения для восстановления положения пространства обзора в перспективной проекции

  1. С полем зрения и аспектом

Поскольку матрица проекции определяется полем зрения и соотношением сторон, можно восстановить положение области просмотра с полем зрения и соотношением сторон. При условии, что это симметричная перспективная проекция и нормализованные координаты устройства, глубина и ближняя и дальняя плоскости известны.

Восстановить расстояние Z в поле зрения:

z_ndc = 2.0 * depth - 1.0;
z_eye = 2.0 * n * f / (f + n - z_ndc * (f - n));

Восстановить положение области просмотра по нормализованным координатам устройства XY:

ndc_x, ndc_y = xy normalized device coordinates in range from (-1, -1) to (1, 1):

viewPos.x = z_eye * ndc_x * aspect * tanFov;
viewPos.y = z_eye * ndc_y * tanFov;
viewPos.z = -z_eye;


2. С матрицей проекции

Параметры проекции, определяемые полем зрения и соотношением сторон, сохраняются в матрице проекции. Поэтому положение окна просмотра можно восстановить по значениям из матрицы проекции из симметричной проекции перспективы.

Обратите внимание на соотношение между матрицей проекции, полем зрения и соотношением сторон:

prjMat[0][0] = 2*n/(r-l) = 1.0 / (tanFov * aspect);
prjMat[1][1] = 2*n/(t-b) = 1.0 / tanFov;

prjMat[2][2] = -(f+n)/(f-n)
prjMat[2][2] = -2*f*n/(f-n)

Восстановить расстояние Z в поле зрения:

A     = prj_mat[2][2];
B     = prj_mat[3][2];
z_ndc = 2.0 * depth - 1.0;
z_eye = B / (A + z_ndc);

Восстановить положение области просмотра по нормализованным координатам устройства XY:

viewPos.x = z_eye * ndc_x / prjMat[0][0];
viewPos.y = z_eye * ndc_y / prjMat[1][1];
viewPos.z = -z_eye;


3. С матрицей обратной проекции

Конечно, положение окна просмотра может быть восстановлено с помощью матрицы обратной проекции.

mat4 inversePrjMat = inverse( prjMat );
vec4 viewPosH      = inversePrjMat * vec4(ndc_x, ndc_y, 2.0*depth - 1.0, 1.0)
vec3 viewPos       = viewPos.xyz / viewPos.w;


Смотрите дальше:

Источник
Другие вопросы по тегам