Как рассчитать размер прямоугольника, который виден камере по заданной координате?

Я сделал небольшое приложение three.js, которое перемещает круг из нижней части холста в верхнюю часть:

let renderer, scene, light, circles, camera;

initialize();
animate();

function initialize() {
  renderer = new THREE.WebGLRenderer({ alpha: true, antialias: true });
  renderer.setSize(window.innerWidth, window.innerHeight);
  document.body.appendChild(renderer.domElement);

  scene = new THREE.Scene();

  light = new THREE.AmbientLight();
  scene.add(light);

  circles = new THREE.Group();
  scene.add(circles);

  camera = new THREE.PerspectiveCamera(45, renderer.domElement.clientWidth / renderer.domElement.clientHeight, 1);
  camera.position.z = circles.position.z + 500;
}


function animate() {
  // Update each circle.
  Array.from(circles.children).forEach(circle => {
    if (circle.position.y < visibleBox(circle.position.z).max.y) {
      circle.position.y += 4;
    } else {
      circles.remove(circle);
    }
  });

  // Create a new circle.
  let circle = new THREE.Mesh();
  circle.geometry = new THREE.CircleGeometry(30, 30);
  circle.material = new THREE.MeshToonMaterial({ color: randomColor(), transparent: true, opacity: 0.5 });
  circle.position.z = _.random(camera.position.z - camera.far, camera.position.z - (camera.far / 10));
  circle.position.x = _.random(visibleBox(circle.position.z).min.x, visibleBox(circle.position.z).max.x);
  circle.position.y = visibleBox(circle.position.z).min.y;
  circles.add(circle);

  // Render the scene.
  renderer.render(scene, camera);
  requestAnimationFrame(animate);
}

function visibleBox(z) {
 return new THREE.Box2(
   new THREE.Vector2(-1000, -1000),
   new THREE.Vector2(1000, 1000)
 );
}

function randomColor() {
  return `#${ _.sampleSize("abcdef0123456789", 6).join("")}`;
}
body {
  width: 100%;
  height: 100%;
  overflow: hidden;
}
<script src="https://cdnjs.cloudflare.com/ajax/libs/three.js/87/three.js">
</script>

<script src="https://cdnjs.cloudflare.com/ajax/libs/lodash.js/4.17.4/lodash.min.js">
</script>

Я использую функцию visibleBox(z) определить, где создать и уничтожить каждый круг. Я жестко закодировал возвращаемое значение для этой функции, но вместо этого я хотел бы, чтобы он вычислял размер прямоугольника, который виден камере на заданной глубине, z,

усеченный

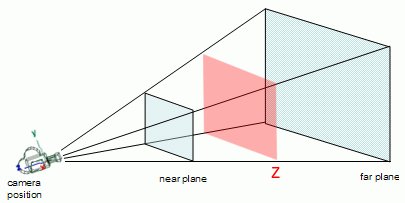
Другими словами, я хочу, чтобы каждый круг создавался точно в нижней части усеченной камеры (нижний край красного прямоугольника на изображении выше) и уничтожался точно, когда он достигал верхней части усеченного конуса (верхний край красный прямоугольник).

Итак, как мне вычислить этот прямоугольник?

Источник

1 ответ

Измените функцию следующим образом:

function visibleBox(z) {
    var t = Math.tan( THREE.Math.degToRad( camera.fov ) / 2 )
    var h = t * 2 * z;
    var w = h * camera.aspect;
    return new THREE.Box2(new THREE.Vector2(-w, h), new THREE.Vector2(w, -h));
}

И установите положение круга следующим образом:

circle.position.z = _.random(-camera.near, -camera.far);
var visBox = visibleBox(circle.position.z)
circle.position.x = _.random(visBox.min.x, visBox.max.x);
circle.position.y = visBox.min.y;

Демонстрация кода:

let renderer, scene, light, circles, camera;

initialize();
animate();

function initialize() {
  renderer = new THREE.WebGLRenderer({ alpha: true, antialias: true });
  renderer.setSize(window.innerWidth, window.innerHeight);
  document.body.appendChild(renderer.domElement);

  scene = new THREE.Scene();

  light = new THREE.AmbientLight();
  scene.add(light);

  circles = new THREE.Group();
  scene.add(circles);

  camera = new THREE.PerspectiveCamera(45, renderer.domElement.clientWidth / renderer.domElement.clientHeight, 1);
  camera.position.z = circles.position.z + 500;
}


function animate() {
  // Update each circle.
  Array.from(circles.children).forEach(circle => {
    if (circle.position.y < visibleBox(circle.position.z).max.y) {
      circle.position.y += 4;
    } else {
      circles.remove(circle);
    }
  });

  // Create a new circle.
  let circle = new THREE.Mesh();
  circle.geometry = new THREE.CircleGeometry(30, 30);
  circle.material = new THREE.MeshToonMaterial({ color: randomColor(), transparent: true, opacity: 0.5 });
  circle.position.z = _.random(-(camera.near+(camera.far-camera.near)/5), -camera.far);
  var visBox = visibleBox(circle.position.z)
  circle.position.x = _.random(visBox.min.x, visBox.max.x);
  circle.position.y = visBox.min.y;
  circles.add(circle);

  // Render the scene.
  renderer.render(scene, camera);
  requestAnimationFrame(animate);
}

function visibleBox(z) {
    var t = Math.tan( THREE.Math.degToRad( camera.fov ) / 2 )
    var h = t * 2 * z;
    var w = h * camera.aspect;
    return new THREE.Box2(new THREE.Vector2(-w, h), new THREE.Vector2(w, -h));
}

function randomColor() {
  return `#${ _.sampleSize("abcdef0123456789", 6).join("")}`;
}
<script src="https://cdnjs.cloudflare.com/ajax/libs/three.js/87/three.js">
</script>

<script src="https://cdnjs.cloudflare.com/ajax/libs/lodash.js/4.17.4/lodash.min.js">
</script>


объяснение

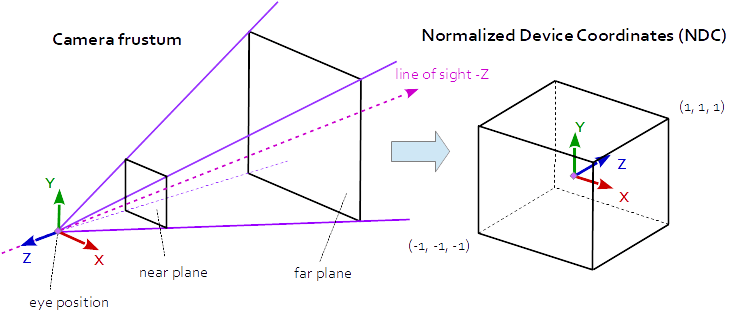
Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Он преобразуется из пространства глаза в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) путем деления на w компонент координат клипа. НДЦ находятся в диапазоне (-1,-1,-1) - (1,1,1).


В перспективной проекции соотношение между значением глубины и расстоянием z до камеры не является линейным.
Матрица перспективной проекции выглядит так:

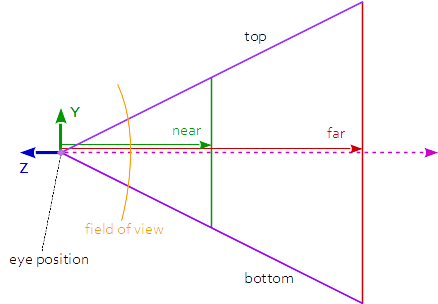
r = right, l = left, b = bottom, t = top, n = near, f = far

2*n/(r-l)      0              0               0
0              2*n/(t-b)      0               0
(r+l)/(r-l)    (t+b)/(t-b)    -(f+n)/(f-n)    -1    
0              0              -2*f*n/(f-n)    0

Из этого следует соотношение между координатой z в пространстве вида и нормализованными координатами устройства z, компонентом и глубиной.

z_ndc = ( -z_eye * (f+n)/(f-n) - 2*f*n/(f-n) ) / -z_eye
depth = (z_ndc + 1.0) / 2.0

Обратная операция выглядит так:

n = near, f = far

z_ndc = 2.0 * depth - 1.0;
z_eye = 2.0 * n * f / (f + n - z_ndc * (f - n));

Если матрица перспективной проекции известна, это можно сделать следующим образом:

A = prj_mat[2][2]
B = prj_mat[3][2]
z_eye = B / (A + z_ndc)

См. Как визуализировать глубину линейно в современном OpenGL с gl_FragCoord.z ​​во фрагментном шейдере?


Реальность между проецируемой областью в пространстве вида и координатой Z пространства вида является линейной. Это зависит от угла поля зрения и соотношения сторон.

Нормализованный размер устройства может быть преобразован в размер в пространстве вида следующим образом:

aspect = w / h
tanFov = tan( fov_y * 0.5 );

size_x = ndx_size_x * (tanFov * aspect) / z_eye;
size_y = ndx_size_y * tanFov / z_eye;

если матрица перспективной проекции известна и проекция симметрична (линия визирования находится в центре области просмотра, а поле обзора не смещено), это можно сделать следующим образом:

size_x = ndx_size_x * / (prj_mat[0][0] * z_eye);
size_y = ndx_size_y * / (prj_mat[1][1] * z_eye);

См. Поле зрения + Соотношение сторон + Матрица вида из матрицы проекции (HMD OST Calibration)


Обратите внимание, что каждая позиция в нормализованных координатах устройства может быть преобразована для просмотра пространственных координат с помощью матрицы обратной проекции:

mat4 inversePrjMat = inverse( prjMat );
vec4 viewPosH      = inversePrjMat * vec3( ndc_x, ndc_y, 2.0 * depth - 1.0, 1.0 );
vec3 viewPos       = viewPos.xyz / viewPos.w;

См. Как восстановить положение пространства вида с учетом значения глубины пространства просмотра и ndc xy


Это означает, что непроецированный прямоугольник с определенной глубиной может быть рассчитан следующим образом:

vec4 viewLowerLeftH  = inversePrjMat * vec3( -1.0, -1.0, 2.0 * depth - 1.0, 1.0 );
vec4 viewUpperRightH = inversePrjMat * vec3(  1.0,  1.0, 2.0 * depth - 1.0, 1.0 );
vec3 viewLowerLeft   = viewLowerLeftH.xyz / viewLowerLeftH.w;
vec3 viewUpperRight  = viewUpperRightH.xyz / viewUpperRightH.w;
Источник
Другие вопросы по тегам