Как визуализировать глубину линейно в современном OpenGL с gl_FragCoord.z во фрагментном шейдере?
Я прочитал много информации о получении глубины с фрагментным шейдером.
такие как
http://www.opengl.org/discussion_boards/ubbthreads.php?ubb=showflat&Number=234519
но я до сих пор не знаю, gl_FragCoord.z является линейным.
Спецификация GLSL гласит, что его диапазон составляет [0,1] в экране, не говоря уже о том, линейный он или нет.
Я думаю, что линейность очень важна, так как я буду использовать визуализированную модель для сопоставления карты глубины от Kinect.
Тогда, если он не линейный, как линеаризовать его в мировом пространстве?
4 ответа
но я до сих пор не знаю, является ли gl_FragCoord.z линейным или нет.
Будь то gl_FragCoord.z является линейным или не зависит от матрицы проекции. В то время как для орфографической проекции gl_FragCoord.z линейный, для перспективной проекции он не линейный.
В общем, глубина (gl_FragCoord.z а также gl_FragDepth) рассчитывается следующим образом (см. GLSL gl_FragCoord.z Расчет и настройка gl_FragDepth):
float ndc_depth = clip_space_pos.z / clip_space_pos.w;
float depth = (((farZ-nearZ) * ndc_depth) + nearZ + farZ) / 2.0;
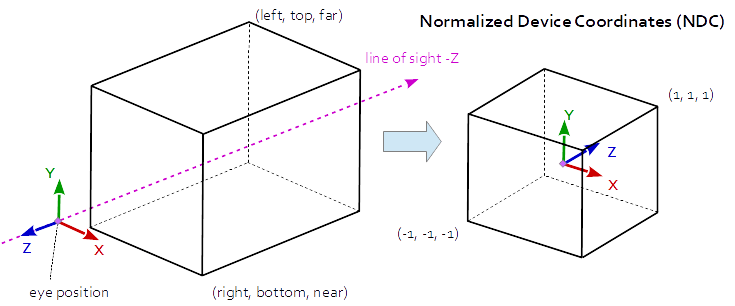
Матрица проекции описывает отображение от трехмерных точек сцены к двухмерным точкам области просмотра. Он преобразуется из пространства глаза в пространство клипа, а координаты в пространстве клипа преобразуются в нормализованные координаты устройства (NDC) путем деления на компонент w координат клипа.
Ортографическая проекция
В ортогональной проекции координаты в глазном пространстве линейно отображаются на нормализованные координаты устройства.
Ортографическая матрица проекции:
r = right, l = left, b = bottom, t = top, n = near, f = far
2/(r-l) 0 0 0
0 2/(t-b) 0 0
0 0 -2/(f-n) 0
-(r+l)/(r-l) -(t+b)/(t-b) -(f+n)/(f-n) 1
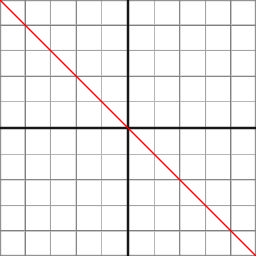
В ортогональной проекции компонент Z вычисляется по линейной функции:
z_ndc = z_eye * -2/(f-n) - (f+n)/(f-n)
Перспективная проекция
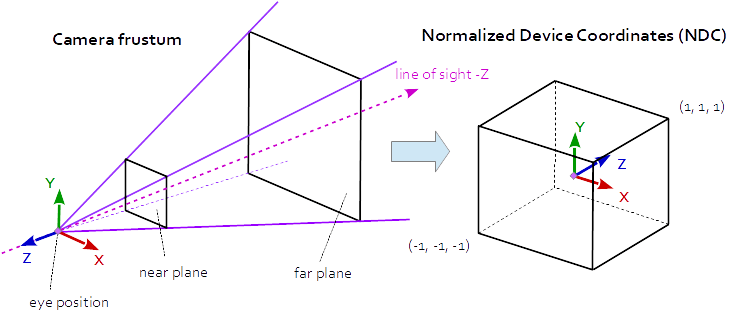
В перспективной проекции матрица проекции описывает отображение из трехмерных точек мира, как они видны с камеры-обскуры, в двухмерные точки видового экрана.
Координаты пространства глаза в усеченной области камеры (усеченная пирамида) отображаются в куб (нормализованные координаты устройства).
Матрица перспективной проекции:
r = right, l = left, b = bottom, t = top, n = near, f = far
2*n/(r-l) 0 0 0
0 2*n/(t-b) 0 0
(r+l)/(r-l) (t+b)/(t-b) -(f+n)/(f-n) -1
0 0 -2*f*n/(f-n) 0
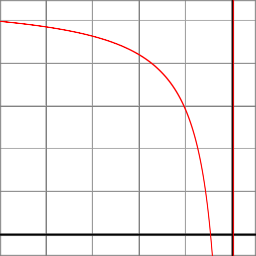
В перспективной проекции Z-компонент вычисляется рациональной функцией:
z_ndc = ( -z_eye * (f+n)/(f-n) - 2*f*n/(f-n) ) / -z_eye
Глубина буфера
Поскольку нормализованные координаты устройства находятся в диапазоне (-1,-1,-1) - (1,1,1), координата Z должна быть сопоставлена с глубиной, находящейся в диапазоне [0,1]:
depth = (z_ndc + 1) / 2
Тогда, если оно не линейно, как линеаризовать его в мировом пространстве?
Чтобы преобразовать глубину буфера глубины в исходную Z-координату, необходимо знать проекцию (ортогональную или перспективную), а также ближнюю и дальнюю плоскости.
Ортографическая проекция
n = near, f = far
z_eye = depth * (f-n) + n;
Перспективная проекция
n = near, f = far
z_ndc = 2.0 * depth - 1.0;
z_eye = 2.0 * n * f / (f + n - z_ndc * (f - n));
Если матрица перспективной проекции известна, это можно сделать следующим образом:
A = prj_mat[2][2]
B = prj_mat[3][2]
z_eye = B / (A + z_ndc)
Смотрите также ответ на
Как только он проецируется, он теряет свою линейность, gl_FragCoord.z не является линейным.
Для возврата к линейному режиму необходимо выполнить 2 шага:
1) преобразовать переменную gl_FragCoord.z на нормализованные координаты устройства в диапазоне [-1, 1]
z = gl_FragCoord.z * 2.0 - 1.0
2) Применить обратную матрицу проекции (IP). (Вы можете использовать произвольные значения для x и y) и нормализовать для последнего компонента.
unprojected = IP * vec4(0, 0, z, 1.0)
unprojected /= unprojected.w
Вы получите точку в пространстве обзора (или пространство камеры, назовите его), у которого есть линейная z между znear и zfar.
Будь то gl_FragCoord.z является линейным или нет, зависит от вашей матрицы преобразования. gl_FragCoord.z определяется путем вычислений gl_Position.z / gl_Position.w для всех вершин вашего треугольника, а затем интерполировать результат по всем фрагментам этого треугольника.
Так gl_FragCoord.z является линейным, когда ваша матрица преобразования присваивает постоянное значение gl_Position.w (что обычно происходит с матрицами ортопроекции) и является нелинейным, когда gl_Position.w зависит от x, y, или же z координата вашего входного вектора (что происходит с матрицами перспективной проекции).
Вам решать, хотите ли вы линейный Z или нет, все зависит от вашей матрицы проекции. Вы можете прочитать это:
http://www.songho.ca/opengl/gl_projectionmatrix.html
Что очень хорошо объясняет, как работает проекционная матрица. Может быть лучше иметь нелинейный Z, чтобы иметь лучшую точность на переднем плане и меньше на заднем плане, артефакты глубины менее заметны вдали...