Как оптимизировать A* (AStar) поиск вогнутых фигур? (включает скриншоты)
Я пишу довольно простую 2D игру. Он использует равномерно распределенную 2D-сетку тайлов для всех данных о столкновениях. Каждая плитка в сетке либо сплошная, либо пустая.
Для поиска пути я использую A* (A Star), и попробовал эвристики Манхэттена и Диагонали (расстояние Чебышева).
В большинстве случаев он работает хорошо, но становится довольно дорогим, когда пытается найти путь к цели, находящейся в углублении вогнутой формы (например, U-образной формы).
Например, на рисунке ниже парень справа найдет путь к парню слева. Вся трава (зелёная, тёмно-зелёная и жёлтая) это пустое место. Единственными сплошными плитками являются коричневые "деревянные" плитки и серые "каменные" плитки, образующие боковую форму буквы "U".

Теперь вот результаты поиска пути (в данном случае A * с Manhattan Heuristics):

Красные и зеленые квадраты отладки показывают, какие плитки были посещены во время поиска A *. Красный - в списке "Закрыто", а зеленый - в списке "Открыть" (согласно спецификации A *). Синяя линия на последнем выбранном пути (что является правильным).
Как видите, поиск был довольно исчерпывающим, посещая множество плиток, создавая почти идеальный круг.
Я понимаю, почему это происходит на основе алгоритма A * и выбранной мной эвристики (когда вы проходите мимо цели вдоль стены, плитки дальше начинают иметь лучшие значения F, заставляя их исследовать, прежде чем вернуться к правильному дорожка). То, что я не знаю, как это сделать лучше:)
Есть предложения о возможных улучшениях? Возможно, другая эвристика? Может быть, другой алгоритм поиска пути все вместе?
Спасибо!
Основываясь на некоторых предложениях, я склоняюсь к обновлению своей реализации A *, чтобы включить улучшения, найденные в HPA *. Исходя из некоторого начального прочтения, кажется, что он будет достаточно хорошо рассматривать случаи, подобные приведенному выше, учитывая правильную степень детализации в иерархии. Я обновлю, как только закончу изучать это.
2 ответа
Я в конечном итоге с помощью динамического HPA*. Я написал подробности о решении здесь:
Вы должны разорвать связи к конечной точке.
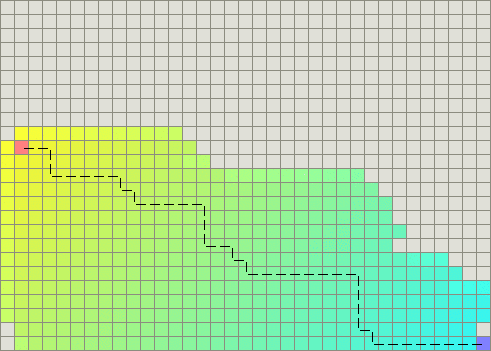
(Без разрыва связей к конечной точке)

(С разрывом связей к конечной точке)

(Пример с препятствием)