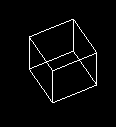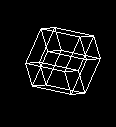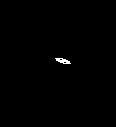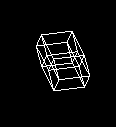Как я должен обрабатывать (морфинг) 4D объектов в OpenGL?
Я хочу попробовать написать детскую площадку, похожую на эти 4D игрушки, поэтому я начал изучать OpenGL.
из моего текущего понимания люди используют VBO и унифицированную матрицу преобразования для в основном статических объектов
(например, кубики, скелетные анимации и т. д., которые обычно включают в себя преобразования)
я также слышал, что при трансформации между моделями также используются VBO для кэширования обеих моделей, поскольку обе они будут четко определены и не так уж много промежуточных.
но в четырехмерных игрушках, упомянутых выше, объекты сильно изменяются и обрезаются.
и вполне вероятно, что нет определенных моделей, и много переходов между ними.
(теперь это может быть простой квадрат, а остроконечный шар подрезается пополам).
в этом случае является ли обновление-вершина-VBO-на-кадр или вершинные массивы (которые я видел в другом вопросе) подходящим решением?
1 ответ
Для начала я бы использовал 4D -> 3D проекция вместо разреза по гиперплоскости. Результат не тот же самый, но он приблизит вас к вашей цели (так что вы можете позже обновить это, чтобы сократить). Так же, как в 3D -> 2D Преобразования, используемые в графике, у вас есть 2 варианта: один использует перспективную проекцию, а второй просто игнорирует 4-ю размерную координату при рендеринге Я буду использовать последний, так как это проще.
сооружения
Чтобы сделать это максимально простым, я буду использовать каркас вместо рендеринга BR. Так что вам нужно обрабатывать 4D сетку (каркас). Я бы использовал 2 таблицы:
double pnt[]; // 4D point list (x,y,z,u) int lin[]; // lines point indexes (i0,i1)Первый хранит все вершины вашей сетки, а второй содержит индексные пары точек, соединенных линиями в каркасном представлении.
прообразы
Если бы я игнорировал только 4-ю координату, мы бы не получили желаемой функциональности. Поэтому, чтобы заставить работать 4-е измерение, нам нужно добавить 4D- преобразование, чтобы ориентировать нашу сетку в 4D-режиме перед рендерингом. Так что используйте однородную матрицу преобразования и позвольте
rep, В 4D должно быть5x5ортонормированная матрица с4x4вращающаяся частьrot,Чтобы сделать это еще проще, избегайте пока плавных поворотов (как в 4D, что не так просто) и вычислите случайное вращение
4x4матрица вместо. Так что просто установите все ячейки случайным образом<-1,+1>, Обрабатывать каждую строку как базовый вектор. Чтобы сделать их ортонормированными, просто сделайте их единичными и используйте перекрестный продукт. Для получения дополнительной информации см.:оказывать
просто конвертируйте таблицу точек по вашей матрице преобразования
(x',y',z',u',W) = rep * (x,y,z,u,1)затем возьмите (х
,y,z`) и рендер...
Вот простой пример OpenGL/C++ 4D гиперкуба:
//---------------------------------------------------------------------------
//--- Mesh 4D: ver 0.000 ----------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _mesh4D_h
#define _mesh4D_h
//---------------------------------------------------------------------------
#include <math.h>
#include "nd_math.h"
#include "list.h"
//---------------------------------------------------------------------------
const double pi = M_PI;
const double pi2 =2.0*M_PI;
const double pipol=0.5*M_PI;
const double deg=M_PI/180.0;
const double rad=180.0/M_PI;
//---------------------------------------------------------------------------
class mesh4D
{
public:
matrix<5> rep; // 4D uniform 5x5 transform matrix
List<double> pnt; // 4D point list (x,y,z,u)
List<int> lin; // lines point indexes (i0,i1)
mesh4D() {}
mesh4D(mesh4D& a) { *this=a; }
~mesh4D() {}
mesh4D* operator = (const mesh4D *a) { *this=*a; return this; }
//mesh4D* operator = (const mesh4D &a) { ...copy... return this; }
void set_randomrep(); // random oriented uniform 4D transform matrix with origin (0,0,0,0)
void set_hypercube(double a);
void draw();
};
//---------------------------------------------------------------------------
void mesh4D::set_randomrep()
{
int i,j;
matrix<4> rot;
rep.unit();
rot.rnd();
rot.orthonormal();
for (i=0;i<4;i++)
for (j=0;j<4;j++)
rep[i][j]=rot[i][j];
}
void mesh4D::set_hypercube(double a)
{
rep.unit(); // reset orientation
pnt.num=0; // clear point list
lin.num=0; // clear line list
pnt.add(-a); pnt.add(-a); pnt.add(-a); pnt.add(-a);
pnt.add(+a); pnt.add(-a); pnt.add(-a); pnt.add(-a);
pnt.add(-a); pnt.add(+a); pnt.add(-a); pnt.add(-a);
pnt.add(+a); pnt.add(+a); pnt.add(-a); pnt.add(-a);
pnt.add(-a); pnt.add(-a); pnt.add(+a); pnt.add(-a);
pnt.add(+a); pnt.add(-a); pnt.add(+a); pnt.add(-a);
pnt.add(-a); pnt.add(+a); pnt.add(+a); pnt.add(-a);
pnt.add(+a); pnt.add(+a); pnt.add(+a); pnt.add(-a);
pnt.add(-a); pnt.add(-a); pnt.add(-a); pnt.add(+a);
pnt.add(+a); pnt.add(-a); pnt.add(-a); pnt.add(+a);
pnt.add(-a); pnt.add(+a); pnt.add(-a); pnt.add(+a);
pnt.add(+a); pnt.add(+a); pnt.add(-a); pnt.add(+a);
pnt.add(-a); pnt.add(-a); pnt.add(+a); pnt.add(+a);
pnt.add(+a); pnt.add(-a); pnt.add(+a); pnt.add(+a);
pnt.add(-a); pnt.add(+a); pnt.add(+a); pnt.add(+a);
pnt.add(+a); pnt.add(+a); pnt.add(+a); pnt.add(+a);
// A0
lin.add( 0+0); lin.add( 0+1);
lin.add( 0+1); lin.add( 0+3);
lin.add( 0+3); lin.add( 0+2);
lin.add( 0+2); lin.add( 0+0);
// A1
lin.add( 4+0); lin.add( 4+1);
lin.add( 4+1); lin.add( 4+3);
lin.add( 4+3); lin.add( 4+2);
lin.add( 4+2); lin.add( 4+0);
// A=A0+A1
lin.add( 0+0); lin.add( 4+0);
lin.add( 0+1); lin.add( 4+1);
lin.add( 0+2); lin.add( 4+2);
lin.add( 0+3); lin.add( 4+3);
// B0
lin.add( 8+0); lin.add( 8+1);
lin.add( 8+1); lin.add( 8+3);
lin.add( 8+3); lin.add( 8+2);
lin.add( 8+2); lin.add( 8+0);
// B1
lin.add(12+0); lin.add(12+1);
lin.add(12+1); lin.add(12+3);
lin.add(12+3); lin.add(12+2);
lin.add(12+2); lin.add(12+0);
// B=B0+B1
lin.add( 8+0); lin.add(12+0);
lin.add( 8+1); lin.add(12+1);
lin.add( 8+2); lin.add(12+2);
lin.add( 8+3); lin.add(12+3);
// hyper cube = A+B
lin.add( 0+0); lin.add( 8+0);
lin.add( 0+1); lin.add( 8+1);
lin.add( 0+2); lin.add( 8+2);
lin.add( 0+3); lin.add( 8+3);
lin.add( 0+4); lin.add( 8+4);
lin.add( 0+5); lin.add( 8+5);
lin.add( 0+6); lin.add( 8+6);
lin.add( 0+7); lin.add( 8+7);
}
//---------------------------------------------------------------------------
void mesh4D::draw()
{
int i,j;
double _zero=1e-3;
vector<5> a,b;
glBegin(GL_LINES);
for (i=0;i<lin.num;)
{
// extrac first point
j=lin[i]*4; i++;
a.a[0]=pnt[j]; j++;
a.a[1]=pnt[j]; j++;
a.a[2]=pnt[j]; j++;
a.a[3]=pnt[j]; j++;
a.a[4]=1.0; // W=1
// extrac second point
j=lin[i]*4; i++;
b.a[0]=pnt[j]; j++;
b.a[1]=pnt[j]; j++;
b.a[2]=pnt[j]; j++;
b.a[3]=pnt[j]; j++;
b.a[4]=1.0; // W=1
// transform
a=rep*a;
b=rep*b;
// render
glVertex3dv(a.a); // use just x,y,z
glVertex3dv(b.a); // use just x,y,z
}
glEnd();
}
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------
Я использовал мою динамику list.h шаблон так:
List<double> xxx; такой же как double xxx[];xxx.add(5); добавляет 5 в конец списка xxx[7] элемент массива доступа (безопасный) xxx.dat[7] доступ к элементу массива (небезопасный, но быстрый прямой доступ) xxx.num фактический используемый размер массива xxx.reset() очищает массив и устанавливает xxx.num=0xxx.allocate(100) предварительно выделить место для 100 Предметы
nd_math.h моя библиотека для N-мерных вычислений. Что вам нужно, это просто 4D,5D вектор и 4x4, 5x5 Математическая математика из линейной алгебры.
Обе библиотеки немного большие по размеру, а также юридические проблемы не позволяют мне поделиться их кодом здесь.
Использование простое:
// globals and init
mesh4D mesh
double animx=-50.0,danimx=0.0;
double animy= 0.0,danimy=2.0;
mesh.set_hypercube(0.5);
// render
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluOrtho2D( -2.0, 2.0, -2.0, 2.0 );
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glRotated(animx,1.0,0.0,0.0);
glRotated(animy,0.0,1.0,0.0);
mesh.draw();
glFlush();
SwapBuffers(hdc);
// some timer
animx+=danimx; if (animx>=360.0) animx-=360.0;
animy+=danimy; if (animy>=360.0) animy-=360.0;
call_render_here();
// on key press or mouse wheel or what ever
mesh.set_randomrep();
И вот предварительный просмотр для некоторых rep вращения...
таким образом, вы можете визуализировать любую каркасную сетку (даже рендеринг BR должен работать таким образом).
Если вы хотите перейти на обрезку, вам нужно взять каждую линию каркаса и вычислить ее пересечение с гиперплоскостью резки. Если мы выбрали гиперплоскость, которая проходит через точку
O(0,0,0,u_cut)
и имеет нормальный
N(0,0,0,1)
Тогда задача значительно упростится. Есть 3 варианта. Рассмотрим граничную линию с конечными точками A,B:
нет пересечения
((A.u > u_cut)&&(B.u > u_cut)) || ((A.u < u_cut)&&(B.u < u_cut))просто игнорировать такой край
1 пересечение
((A.u >= u_cut)&&(B.u <= u_cut)) || ((A.u <= u_cut)&&(B.u >= u_cut))поэтому вычислить пересечение с помощью линейной интерполяции
x = A.x + (B.x-A.x)*(u_cut-A.u)/(B.u-A.u) y = A.y + (B.y-A.y)*(u_cut-A.u)/(B.u-A.u) z = A.z + (B.z-A.z)*(u_cut-A.u)/(B.u-A.u)и помните такую точку, а также край, которому он принадлежит.
полностью внутри
(A.u == u_cut)&&(B.u == u_cut)просто запомните обе конечные точки, а также визуализируйте этот край.
После того как все ребра обработаны таким образом, вам нужно проанализировать запомненные точки пересечения и создать из них новые ребра на основе информации о соединении между ребрами. Я еще этого не делал, поэтому не могу помочь с этим. Я бы попытался соединить запомненные точки с одним соседом, но не уверен, что этого достаточно в 4D.
Для получения дополнительной информации взгляните на соответствующие QA, которые я только что нашел:
[Edit1] код с перспективой
//---------------------------------------------------------------------------
//--- Mesh 4D: ver 0.001 ----------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _mesh4D_h
#define _mesh4D_h
//---------------------------------------------------------------------------
#include <math.h>
#include "nd_math.h"
#include "list.h"
//---------------------------------------------------------------------------
const double pi = M_PI;
const double pi2 =2.0*M_PI;
const double pipol=0.5*M_PI;
const double deg=M_PI/180.0;
const double rad=180.0/M_PI;
//---------------------------------------------------------------------------
class mesh4D
{
public:
matrix<5> rep; // 4D uniform 5x5 transform matrix
List<double> pnt; // 4D point list (x,y,z,u)
List<int> lin; // lines point indexes (i0,i1)
mesh4D() {}
mesh4D(mesh4D& a) { *this=a; }
~mesh4D() {}
mesh4D* operator = (const mesh4D *a) { *this=*a; return this; }
//mesh4D* operator = (const mesh4D &a) { ...copy... return this; }
void set_randomrep(); // random oriented uniform 4D transform matrix with origin (0,0,0,0)
void set_hypercube(double a);
void draw();
};
//---------------------------------------------------------------------------
void mesh4D::set_randomrep()
{
int i,j;
matrix<4> rot;
rot.rnd();
rot.orthonormal();
for (i=0;i<4;i++)
for (j=0;j<4;j++)
rep[i][j]=rot[i][j];
}
//---------------------------------------------------------------------------
void mesh4D::set_hypercube(double a)
{
rep.unit(); // reset orientation
rep[0][4]=0.0; // set position
rep[1][4]=0.0;
rep[2][4]=0.0;
rep[3][4]=3.0*a;
pnt.num=0; // clear point list
lin.num=0; // clear line list
pnt.add(-a); pnt.add(-a); pnt.add(-a); pnt.add(-a);
pnt.add(+a); pnt.add(-a); pnt.add(-a); pnt.add(-a);
pnt.add(-a); pnt.add(+a); pnt.add(-a); pnt.add(-a);
pnt.add(+a); pnt.add(+a); pnt.add(-a); pnt.add(-a);
pnt.add(-a); pnt.add(-a); pnt.add(+a); pnt.add(-a);
pnt.add(+a); pnt.add(-a); pnt.add(+a); pnt.add(-a);
pnt.add(-a); pnt.add(+a); pnt.add(+a); pnt.add(-a);
pnt.add(+a); pnt.add(+a); pnt.add(+a); pnt.add(-a);
pnt.add(-a); pnt.add(-a); pnt.add(-a); pnt.add(+a);
pnt.add(+a); pnt.add(-a); pnt.add(-a); pnt.add(+a);
pnt.add(-a); pnt.add(+a); pnt.add(-a); pnt.add(+a);
pnt.add(+a); pnt.add(+a); pnt.add(-a); pnt.add(+a);
pnt.add(-a); pnt.add(-a); pnt.add(+a); pnt.add(+a);
pnt.add(+a); pnt.add(-a); pnt.add(+a); pnt.add(+a);
pnt.add(-a); pnt.add(+a); pnt.add(+a); pnt.add(+a);
pnt.add(+a); pnt.add(+a); pnt.add(+a); pnt.add(+a);
// A0
lin.add( 0+0); lin.add( 0+1);
lin.add( 0+1); lin.add( 0+3);
lin.add( 0+3); lin.add( 0+2);
lin.add( 0+2); lin.add( 0+0);
// A1
lin.add( 4+0); lin.add( 4+1);
lin.add( 4+1); lin.add( 4+3);
lin.add( 4+3); lin.add( 4+2);
lin.add( 4+2); lin.add( 4+0);
// A=A0+A1
lin.add( 0+0); lin.add( 4+0);
lin.add( 0+1); lin.add( 4+1);
lin.add( 0+2); lin.add( 4+2);
lin.add( 0+3); lin.add( 4+3);
// B0
lin.add( 8+0); lin.add( 8+1);
lin.add( 8+1); lin.add( 8+3);
lin.add( 8+3); lin.add( 8+2);
lin.add( 8+2); lin.add( 8+0);
// B1
lin.add(12+0); lin.add(12+1);
lin.add(12+1); lin.add(12+3);
lin.add(12+3); lin.add(12+2);
lin.add(12+2); lin.add(12+0);
// B=B0+B1
lin.add( 8+0); lin.add(12+0);
lin.add( 8+1); lin.add(12+1);
lin.add( 8+2); lin.add(12+2);
lin.add( 8+3); lin.add(12+3);
// hyper cube = A+B
lin.add( 0+0); lin.add( 8+0);
lin.add( 0+1); lin.add( 8+1);
lin.add( 0+2); lin.add( 8+2);
lin.add( 0+3); lin.add( 8+3);
lin.add( 0+4); lin.add( 8+4);
lin.add( 0+5); lin.add( 8+5);
lin.add( 0+6); lin.add( 8+6);
lin.add( 0+7); lin.add( 8+7);
}
//---------------------------------------------------------------------------
void mesh4D::draw()
{
int i,j;
const double _zero=1e-3;
double focal_length=1.0;
vector<5> a,b;
glBegin(GL_LINES);
for (i=0;i<lin.num;)
{
// extrac first point
j=lin[i]*4; i++;
a.a[0]=pnt[j]; j++;
a.a[1]=pnt[j]; j++;
a.a[2]=pnt[j]; j++;
a.a[3]=pnt[j]; j++;
a.a[4]=1.0; // W=1
// extrac second point
j=lin[i]*4; i++;
b.a[0]=pnt[j]; j++;
b.a[1]=pnt[j]; j++;
b.a[2]=pnt[j]; j++;
b.a[3]=pnt[j]; j++;
b.a[4]=1.0; // W=1
// transform
a=rep*a;
b=rep*b;
// perspective: camera projection plane u=0, focus at (0,0,0,-focal_length)
if (a[3]>=0.0) a*=divide(focal_length,a[3]+focal_length); else a.zero();
if (b[3]>=0.0) b*=divide(focal_length,b[3]+focal_length); else b.zero();
// render
glVertex3dv(a.a); // use just x,y,z
glVertex3dv(b.a); // use just x,y,z
}
glEnd();
}
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------
И предварительный просмотр:
[Edit2] сплошная сетка и поперечное сечение
поэтому я немного изменил архитектуру. Я переместил 4D 5x5 матрица однородного преобразования (reper4D) для разделения файла и добавления цветов и определения сетки с помощью 4D симплексов (4 точки 4 боковых тетраэдра). Разрез - это просто вычисление пересечения (как описано выше) симплекса и разрезания гиперплоскости, в результате чего получаются либо 3 точки (треугольник), 4 точки (тетраэдр) или 0 точек. Который может быть легко отрисован (не нужно анализировать связи между ребрами). Для получения дополнительной информации см. Это:
Btw. Я думаю, что так работает Miegakure. Вот обновленный код:
//---------------------------------------------------------------------------
//--- Mesh 4D: ver 1.000 ----------------------------------------------------
//---------------------------------------------------------------------------
#ifndef _mesh4D_h
#define _mesh4D_h
//---------------------------------------------------------------------------
#include "list.h"
#include "reper4D.h"
//---------------------------------------------------------------------------
class mesh4D
{
public:
reper4D rep; // 4D uniform 5x5 transform matrix
List<double> pnt; // 4D point list (x,y,z,w)
List<int> lin; // 4D wireframe (i0,i1)
List<int> fac; // 4D simplexes (i0,i1,i2,i3)
List<DWORD> col; // simplex colors (RGB)
mesh4D() {}
mesh4D(mesh4D& a) { *this=a; }
~mesh4D() {}
mesh4D* operator = (const mesh4D *a) { *this=*a; return this; }
//mesh4D* operator = (const mesh4D &a) { ...copy... return this; }
void set_hypercube(double a);
void draw_cut(double w_cut); // render cross section by w=w_cut hyperplane
void draw (double focal_length=-1.0,double w_near=-1.0); // render mesh (focal_length<0) -> no perspective, else perspective view in W+ direction
void draw_wireframe(double focal_length=-1.0,double w_near=-1.0); // render wireframe (focal_length<0) -> no perspective, else perspective view in W+ direction
};
//---------------------------------------------------------------------------
void mesh4D::set_hypercube(double a)
{
const double tab_pnt[]=
{
-a, -a, -a, -a,
+a, -a, -a, -a,
-a, +a, -a, -a,
+a, +a, -a, -a,
-a, -a, +a, -a,
+a, -a, +a, -a,
-a, +a, +a, -a,
+a, +a, +a, -a,
-a, -a, -a, +a,
+a, -a, -a, +a,
-a, +a, -a, +a,
+a, +a, -a, +a,
-a, -a, +a, +a,
+a, -a, +a, +a,
-a, +a, +a, +a,
+a, +a, +a, +a,
};
const int tab_lin[]=
{
// A0
0+0, 0+1,
0+1, 0+3,
0+3, 0+2,
0+2, 0+0,
// A1
4+0, 4+1,
4+1, 4+3,
4+3, 4+2,
4+2, 4+0,
// A=A0+A1
0+0, 4+0,
0+1, 4+1,
0+2, 4+2,
0+3, 4+3,
// B0
8+0, 8+1,
8+1, 8+3,
8+3, 8+2,
8+2, 8+0,
// B1
12+0, 12+1,
12+1, 12+3,
12+3, 12+2,
12+2, 12+0,
// B=B0+B1
8+0, 12+0,
8+1, 12+1,
8+2, 12+2,
8+3, 12+3,
// hyper cube = A+B
0+0, 8+0,
0+1, 8+1,
0+2, 8+2,
0+3, 8+3,
0+4, 8+4,
0+5, 8+5,
0+6, 8+6,
0+7, 8+7,
};
// 5x simplex per cube
#define _cube(a0,a1,a2,a3,a4,a5,a6,a7) a1,a2,a4,a7, a0,a1,a2,a4, a2,a4,a6,a7, a1,a2,a3,a7, a1,a4,a5,a7
// 4D hypercube = 8 cubes
const int tab_fac[]=
{
_cube( 0, 1, 2, 3, 4, 5, 6, 7),
_cube( 0, 1, 2, 3, 8, 9,10,11),
_cube( 4, 5, 6, 7,12,13,14,15),
_cube( 8, 9,10,11,12,13,14,15),
_cube( 0, 1, 4, 5, 8, 9,12,13),
_cube( 0, 2, 4, 6, 8,10,12,14),
_cube( 1, 3, 5, 7, 9,11,13,15),
_cube( 2, 3, 6, 7,10,11,14,15),
};
#undef _cube
const DWORD tab_col[]=
{
// BBGGRR, BBGGRR, BBGGRR, BBGGRR, BBGGRR,
0x00FF0000,0x00FF0000,0x00FF0000,0x00FF0000,0x00FF0000,
0x0000FF00,0x0000FF00,0x0000FF00,0x0000FF00,0x0000FF00,
0x000000FF,0x000000FF,0x000000FF,0x000000FF,0x000000FF,
0x0000FFFF,0x0000FFFF,0x0000FFFF,0x0000FFFF,0x0000FFFF,
0x00FF00FF,0x00FF00FF,0x00FF00FF,0x00FF00FF,0x00FF00FF,
0x00FFFF00,0x00FFFF00,0x00FFFF00,0x00FFFF00,0x00FFFF00,
0x00FFFFFF,0x00FFFFFF,0x00FFFFFF,0x00FFFFFF,0x00FFFFFF,
0x004080FF,0x004080FF,0x004080FF,0x004080FF,0x004080FF,
};
int i,n;
vector<4> p;
rep.reset();
pnt.num=0; for (i=0,n=sizeof(tab_pnt)/sizeof(tab_pnt[0]);i<n;i++) pnt.add(tab_pnt[i]);
lin.num=0; for (i=0,n=sizeof(tab_lin)/sizeof(tab_lin[0]);i<n;i++) lin.add(tab_lin[i]);
fac.num=0; for (i=0,n=sizeof(tab_fac)/sizeof(tab_fac[0]);i<n;i++) fac.add(tab_fac[i]);
col.num=0; for (i=0,n=sizeof(tab_col)/sizeof(tab_col[0]);i<n;i++) col.add(tab_col[i]);
}
//---------------------------------------------------------------------------
void mesh4D::draw_cut(double w_cut)
{
const double _zero=1e-6;
const int edge2[]={0,1,0,2,0,3,1,2,2,3,3,1,-1}; // simplex wireframe i0,i1
const int edge3[]={0,1,2,3,0,1,3,1,2,3,2,0,-1}; // simplex triangles i0,i1,i2
int e,i,j,k,k0,k1,k2,inside[4];
DWORD rgb;
vector<4> p[4],q[4];
vector<3> xyz[4],nor,a,b;
for (i=0;i<fac.num;)
{
rgb=col[i>>2];
// extrac points (x,y,z,w)
for (k=0;k<4;k++)
{
j=fac[i]*4; i++;
p[k].a[0]=pnt[j]; j++;
p[k].a[1]=pnt[j]; j++;
p[k].a[2]=pnt[j]; j++;
p[k].a[3]=pnt[j]; j++;
// transform
rep.l2g(p[k],p[k]);
inside[k]=1;
}
// process edge2 and compute cross section cut intersection points
for (e=0,k=0;edge2[e]>=0;)
{
k0=edge2[e]; e++;
k1=edge2[e]; e++;
// fully inside
if (fabs(p[k0][3]-w_cut)+fabs(p[k1][3]-w_cut)<=_zero)
{
if ((k<4)&&(inside[k0])){ q[k]=p[k0]; k++; inside[k0]=0; }
if ((k<4)&&(inside[k1])){ q[k]=p[k1]; k++; inside[k1]=0; }
continue;
}
// no intersection
if (((p[k0][3]> w_cut)&&(p[k1][3]> w_cut))||((p[k0][3]< w_cut)&&(p[k1][3]< w_cut))) continue;
// 1 intersection
if (k<4)
{
q[k]=p[k1]-p[k0];
q[k]*=divide(w_cut-p[k0][3],p[k1][3]-p[k0][3]);
q[k]+=p[k0];
q[k][3]=w_cut;
k++;
continue;
}
}
// 4D -> 3D vector
for (k0=0;k0<k;k0++) for (k1=0;k1<3;k1++) xyz[k0][k1]=q[k0][k1];
// render triangle
if (k==3)
{
// normal
a=xyz[1]-xyz[0];
b=xyz[2]-xyz[1];
nor.cross(a,b);
nor.unit();
// render
glBegin(GL_TRIANGLES);
glNormal3dv(nor.a);
glColor4ubv((BYTE*)(&rgb));
glVertex3dv(xyz[0].a);
glVertex3dv(xyz[1].a);
glVertex3dv(xyz[2].a);
glEnd();
}
// render simplex
if (k==4)
for (e=0;edge3[e]>=0;)
{
k0=edge3[e]; e++;
k1=edge3[e]; e++;
k2=edge3[e]; e++;
// normal
a=xyz[k1]-xyz[k0];
b=xyz[k2]-xyz[k1];
nor.cross(a,b);
nor.unit();
// render
glBegin(GL_TRIANGLES);
glNormal3dv(nor.a);
glColor4ubv((BYTE*)(&rgb));
glVertex3dv(xyz[k0].a);
glVertex3dv(xyz[k1].a);
glVertex3dv(xyz[k2].a);
glEnd();
}
}
}
//---------------------------------------------------------------------------
void mesh4D::draw(double focal_length,double w_near)
{
const int edge3[]={0,1,2,3,0,1,3,1,2,3,2,0,-1}; // simplex triangles i0,i1,i2
int i,j,k,k0,k1,k2;
DWORD rgb;
vector<4> p;
vector<3> xyz[4],nor,a,b;
// 4D simplexes
glColor3f(0.3,0.3,0.3);
for (i=0;i<fac.num;)
{
rgb=col[i>>2];
// extrac points (x,y,z,w)
for (k=0;k<4;k++)
{
j=fac[i]*4; i++;
p[0]=pnt[j]; j++;
p[1]=pnt[j]; j++;
p[2]=pnt[j]; j++;
p[3]=pnt[j]; j++;
// transform
rep.l2g(p,p);
// perspective projection
if (focal_length>0.0)
{
p[3]-=w_near;
if (p[3]>=0.0) p*=divide(focal_length,p[3]+focal_length); else p.zero();
}
// 4D -> 3D vector
xyz[k].ld(p[0],p[1],p[2]);
}
// render simplex
for (k=0;edge3[k]>=0;)
{
k0=edge3[k]; k++;
k1=edge3[k]; k++;
k2=edge3[k]; k++;
// normal
a=xyz[k1]-xyz[k0];
b=xyz[k2]-xyz[k1];
nor.cross(a,b);
nor.unit();
// render
// glBegin(GL_LINE_LOOP);
glBegin(GL_TRIANGLES);
glNormal3dv(nor.a);
glColor4ubv((BYTE*)(&rgb));
glVertex3dv(xyz[k0].a);
glVertex3dv(xyz[k1].a);
glVertex3dv(xyz[k2].a);
glEnd();
}
}
}
//---------------------------------------------------------------------------
void mesh4D::draw_wireframe(double focal_length,double w_near)
{
int i,j,k;
vector<4> p[4];
// 4D wireframe
glColor3f(1.0,1.0,1.0);
glBegin(GL_LINES);
for (i=0;i<lin.num;)
{
// extrac points (x,y,z,w)
for (k=0;k<2;k++)
{
j=lin[i]*4; i++;
p[k].a[0]=pnt[j]; j++;
p[k].a[1]=pnt[j]; j++;
p[k].a[2]=pnt[j]; j++;
p[k].a[3]=pnt[j]; j++;
// transform
rep.l2g(p[k],p[k]);
// perspective projection
if (focal_length>0.0)
{
p[k][3]-=w_near;
if (p[k][3]>=0.0) p[k]*=divide(focal_length,p[k][3]+focal_length); else p[k].zero();
}
// render
glVertex3dv(p[k].a); // use just x,y,z
}
}
glEnd();
}
//---------------------------------------------------------------------------
#endif
//---------------------------------------------------------------------------
И предварительный просмотр для рендера сечения:
Хуже всего было определить гиперкуб как набор симплексов...