4D в 3D перспективная проекция

Question

Я пытаюсь рассчитать положение 4D точки в 3D мире. Я начал с 2D и попытался расширить его до 3D, а затем до 4D. Во-первых, я обнаружил, что легко рассчитать проецируемое положение 2D-точки на линии.

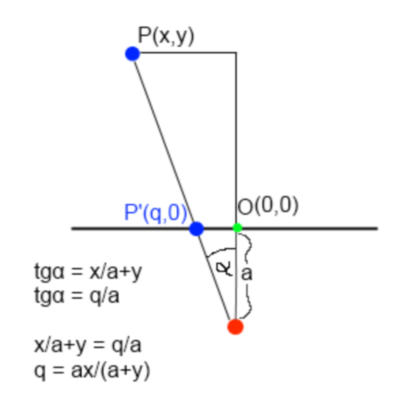
Whoops, there should be () in the first equation: x/(a+y)

Теперь я понял, что то же самое будет применяться в трехмерном мире, если я разделю P(X,Y,Z) на P1(X,Z) и P2(Y,Z), вычислю их Q и затем построю точку P'(Q1,Q2) (Предполагая, что я смотрю положительную бесконечность оси Z из точки C(0,-a) и рендеринг в плоскость XY).

nx = (a*x)/(a+z);
ny = (a*y)/(a+z);

Тогда я подумал, что это так же просто, как добавить следующую точку P3, и придумал

nx = (a*x)/(a+z);
ny = (a*y)/(a+z);
nw = (a*w)/(a+z);

Я чувствовал, что это было странно, потому что W (новая ось) фактически влияет только на Z последней точки, и, ссылаясь на тессеракт, это должно влиять на все измерения...

Это не работает, поэтому я хотел бы спросить, можете ли вы предоставить некоторые детали того, что я делаю неправильно. Я уверен, что это проблема "расщепления точек", и уравнение должно быть более сложным. Пожалуйста, не атакуйте меня матрицами и кватернионами. Я просто хочу иметь простую статическую камеру в (0,-1), глядя на (0,0)...

Спасибо за любую помощь!

Answer 1

• в 2D (x, y) проекция на y=0 означает пересечение линии с линией:
  

  x'/a = x/(a+y)
  

• в 3D (x, y, z) проекция на z=0 означает пересечение линии с плоскостью:
  

  for y=0: x'/a = x/(a+z)
  for x=0: y'/a = y/(a+z)
  

• в 4D (x,y,z,w) проекция на w=0 означает пересечение линии с гиперплоскостью:
  

  for y=0, z=0: x'/a = x/(a+w)
  for x=0, z=0: y'/a = y/(a+w)
  for x=0, y=0: z'/a = z/(a+w)
  

• ...и так далее

В качестве альтернативы можно вычислить пересечение линии и гиперплоскости, используя форму параметра, где линия описывается:

[px,py,pz,pw] = [p0x,p0y,p0z,p0w] + t * [p1x,p1y,p1z,p1w]

где параметр t является любым числом

Гиперплоскость описывается:

[hx,hy,hz,hw] = [h0x,h0y,h0z,h0w] + a * [h1x,h1y,h1z,h1w] + b * [h2x,h2y,h2z,h2w] + c * [h3x,h3y,h3z,h3w]

Теперь точку пересечения можно найти, решив:

[px,py,pz,pw] = [hx,hy,hz,hw]

или более явно:

[p0x,p0y,p0z,p0w] + t * [p1x,p1y,p1z,p1w] = [h0x,h0y,h0z,h0w] + a * [h1x,h1y,h1z,h1w] + b * [h2x,h2y,h2z,h2w] + c * [h3x,h3y,h3z,h3w]

Существует 4 уравнения (по одному для каждого измерения x,y,z,w) и 4 неизвестных (a,b,c,t), которые можно решить, если прямая не параллельна гиперплоскости.

Вышеприведенные мысли являются предметом аналитической геометрии в 4D (где компонент w представляет собой отдельное отдельное измерение), и их не следует смешивать с однородными координатами (где w Компонент используется для интеграции перевода / проецирования в 4D матрицы и отбрасывается в конце графического конвейера с помощью деления перспективы).