Можно ли сделать реалистичное моделирование солнечной системы n-тела в зависимости от размера и массы?

Question

Важное примечание: этот вопрос совершенно не имеет отношения к "PhysX", который является системой физики компьютерных игр (полезен для физики в аркадных играх, таких как игры с мячом и т. Д.); PhysX - это система, встроенная в Unity3D и другие игровые движки; PhysX здесь совершенно неактуален.

//////////////////// ОБНОВЛЕНИЕ (сначала прочитайте внизу) /////////////////////

Я регистрировал значения и искал, где именно проблема, и я думаю, что нашел ее. У меня есть что-то подобное в моем коде

Velocity += Acceleration * Time.deltaTime;
position += Velocity * Time.deltaTime;

Ускорение что-то вроде 0,0000000000000009.. прямо сейчас. Поскольку код течет, скорость увеличивается, как и должно быть, никаких проблем с плавающей точкой. Но в начале, начальное положение земли (0,0,23500f). Вы можете увидеть это на графике, который я дал в конце.

Что ж, теперь, когда я добавляю speed * timedelta (что-то вроде 0,00000000000000005 на данный момент) к позиции, равной 23500, он, по сути, не добавляет ее. позиция по-прежнему (0, 0, 23500) не похожа на (0,0, 23500.00000000000005), поэтому земля не движется, поэтому ускорение не меняется.

Если я установлю начальное положение земли на 0,0,0 и до сих пор, установите ускорение на 0,0000000000000000009, чтобы предположить, что его позиция равна (0,0,23500). Затем он "добавляет" скорость * timedelta. Это становится чем-то вроде (0,0,000000000000000000005) и продолжает расти. Когда значение с плавающей точкой равно 0, нет проблем с добавлением такого небольшого значения. Но если число с плавающей точкой - что-то вроде 23500, то оно не складывает маленькие значения.

Я не знаю, является ли это проблемой единства или поплавком C#.

И именно поэтому я не могу заставить его работать с небольшими значениями. Если я смогу преодолеть это, моя проблема будет решена.

////////////////////////////////////////////////// /////////////////////////////

я развивал физику n-тела, чтобы моделировать нашу солнечную систему, поэтому я собирал данные, чтобы сделать ее максимально реалистичной. Но есть проблема с размером данных. Я искал каждый крошечный кусочек интернета и не смог найти единственного объяснения того, как люди преодолевают это. (Если они так), так что я пытаюсь выстрелить здесь.

Таким образом, чтобы сохранить соотношение расстояния, радиуса и "массы" между планетами, я создал файл excel для вычисления всех данных. (Потому что, чёрт возьми, кто-то выложит "какую массу Земли будет, если у нее есть" эта "диаграмма радиуса" в интернете?) Я дам ss в качестве приложения. По сути, он "нормализует" или, другими словами, "масштабирует" каждое свойство планеты до заданной ссылки. В этом случае я взял ссылку как "радиус Земли".

Я работаю в единстве, и вы знаете, вы не можете работать с "слишком большими" или "слишком маленькими" ценностями в единстве. Поэтому мне пришлось уменьшить масштаб Солнечной системы, "много!"

Поэтому я использую закон всемирного тяготения Ньютона, который является F = GMm/r^2, чтобы упростить его, я непосредственно вычисляю a = GM/r^2 для данного тела из всех других тел.

Таким образом, реальное значение гравитационного ускорения Земли "к Солнцу" составляет примерно 0,000006 км / с ^ 2, что даже невероятно мало, чтобы работать в единстве, но это может сработать. Тем не менее, чтобы получить это значение,1 мне нужно установить радиус Земли (масштаб) равным 6371 единице, а Солнца - масштаб 696 342!, что СЛИШКОМ велико, чтобы сделать его единым целым.

Итак, я сказал, пусть радиус Земли будет 1, в единицах единицы. Итак, когда радиус меняется, все меняется, масса, расстояние... Я сохранил плотность планеты и рассчитал массу из нового объема с новым радиусом. Все расчеты в приложении.

Итак, дело в том, что когда я принимаю радиус Земли за 1, гравитационное ускорение к Солнцу становится чем-то вроде 0,0000000000009, что смехотворно мало. И, конечно, Unity не работает с этим значением.

Так что, если я вместо этого увеличу радиус Земли, тогда масса и радиус Солнца станут смехотворно большими, и опять же, я не смогу с этим работать.

Я не знаю, как другие люди исправили это, что они сделали, чтобы преодолеть эту проблему, но, как я вижу отсюда, кажется невозможным сделать реалистичное моделирование Солнечной системы в n-теле. (по крайней мере, в единстве)

Поэтому мне нужно иметь 10 представителей для публикации изображений -_-, вместо этого я дам ссылку. http://berkaydursun.com/solar_system_simulator/data.PNG Также одним из каталогов является рабочая экспериментальная имитация солнечной системы с вычислениями n-тел, но с нереальными значениями. Он работает довольно хорошо, и даже выглядит как-то близко к реальному, но нет, у него нет правильных соотношений ^^ Вы можете проверить это здесь, если хотите http://berkaydursun.com/solar_system_simulator/

Редактировать: WoW Я почти начал каждый абзац с "Так" ^^

Answer 1

Я также запрограммировал симуляцию системы Sol, так что вот мое понимание:

1. оказание

   Я использую OpenGL с масштабированием 1:1. Все единицы в СИ, т. Е. [М, с, кг,...]. Проблема начинается с Z-буфера. Обычный бит Z-буфера 16/24/32 bit что далеко не то, что вам нужно. Я рендеринг от 0,1 м до 1000 а.е., так как это преодолеть?

   Я справился с этим, выполнив рендеринг с 3-мя усеченными элементами одновременно, используя Z-сортировку и Z-буферизацию (Z-сортировка необходима из-за прозрачных колец... и других эффектов). Итак, сначала я отрисовываю самые отдаленные части до zfar=1000AU, Небесный купол проецируется на z=750AU расстояние, затем очистите Z-буфер и визуализируйте объекты до zfar=0.1AU, Затем снова очистите Z-буфер и визуализируйте близкие объекты до zfar=100000 m,

   Чтобы получить эту работу, вы должны иметь максимально точную матрицу проекции. gluPerspective имеет неточные котангины, поэтому он должен отремонтировать соответствующие элементы (заставьте меня долго это замечать). Z near значение зависит от ширины битов Z-буфера. При правильном кодировании это работает хорошо даже с зумом 10000x, Я использую эту программу в качестве навигации / поисковика объектов для моего телескопа:) в режиме реального времени из моего домашнего просмотра. Я объединяю трехмерные звезды, космические тела, корабли, реальную землю (через DTM и спутниковую текстуру). Он способен даже на вывод красно-голубого анаглифа:). Может рендериться с поверхности, из атмосферы, из космоса... (не только привязанный к Земле). Никакая другая сторонняя библиотека, кроме OpenGL, не используется. Вот как это выглядит:

   

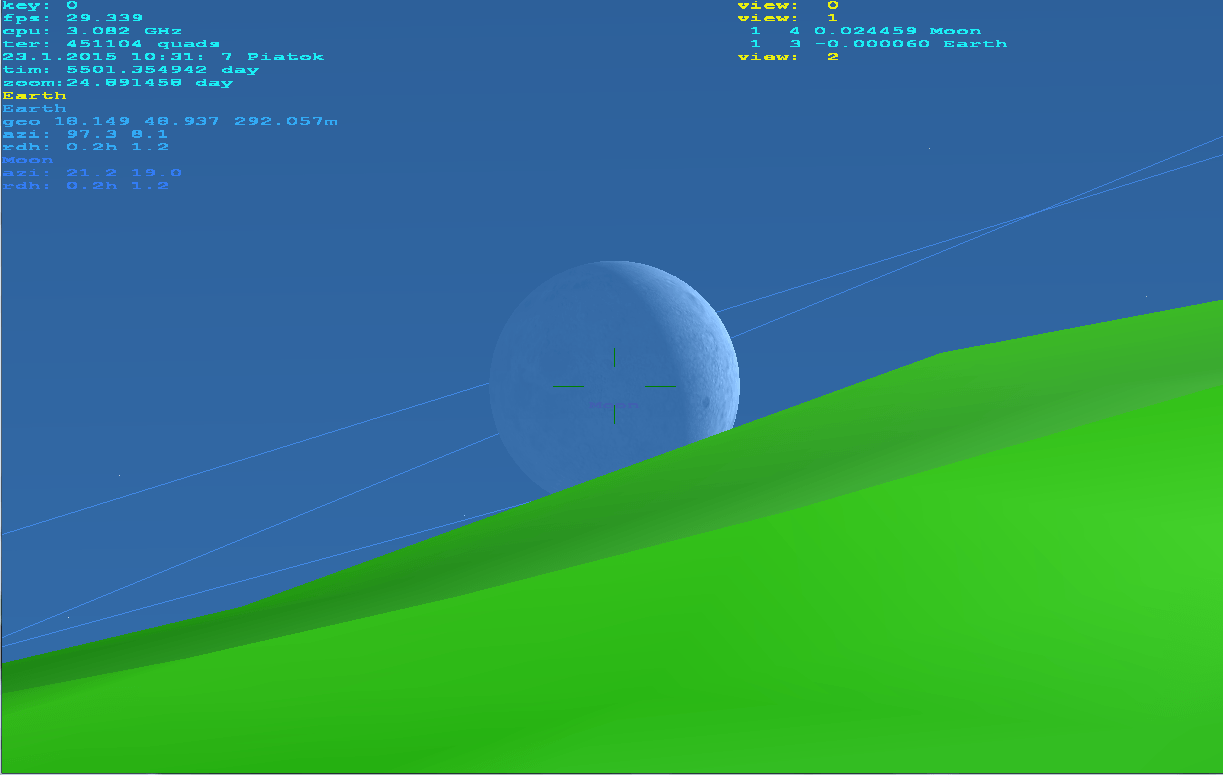
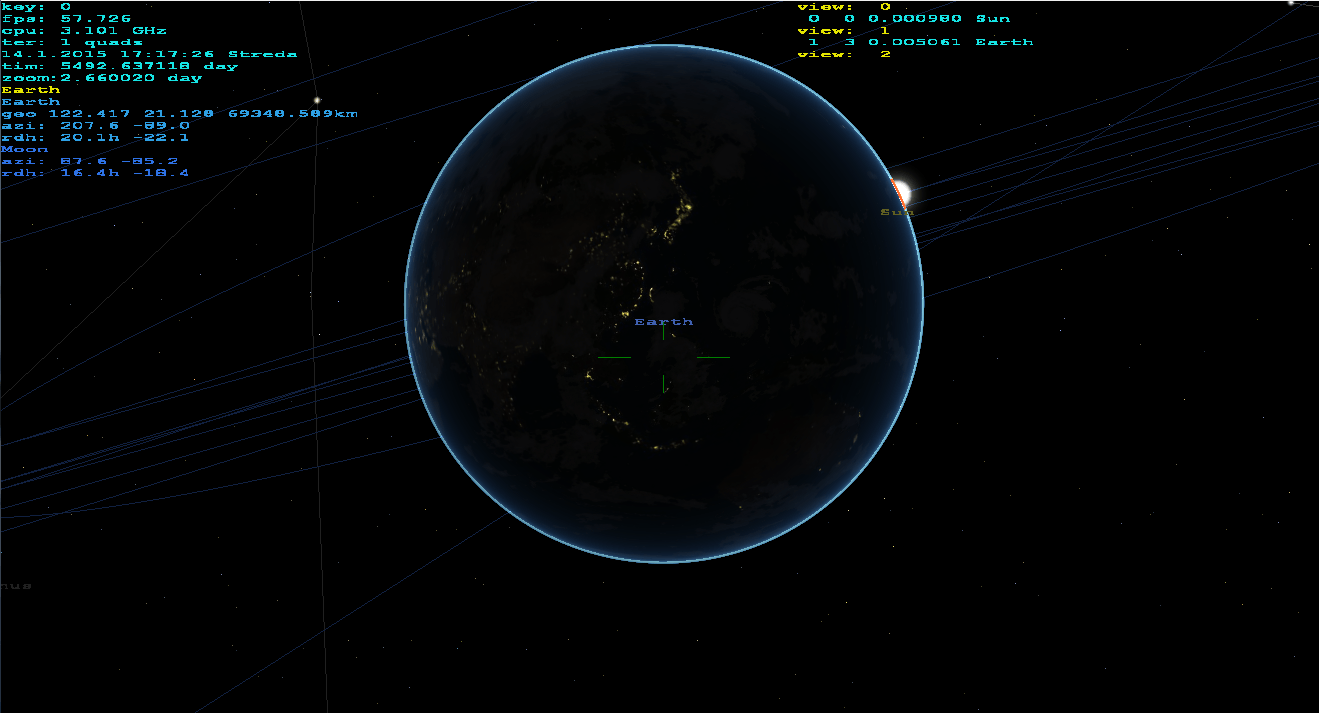
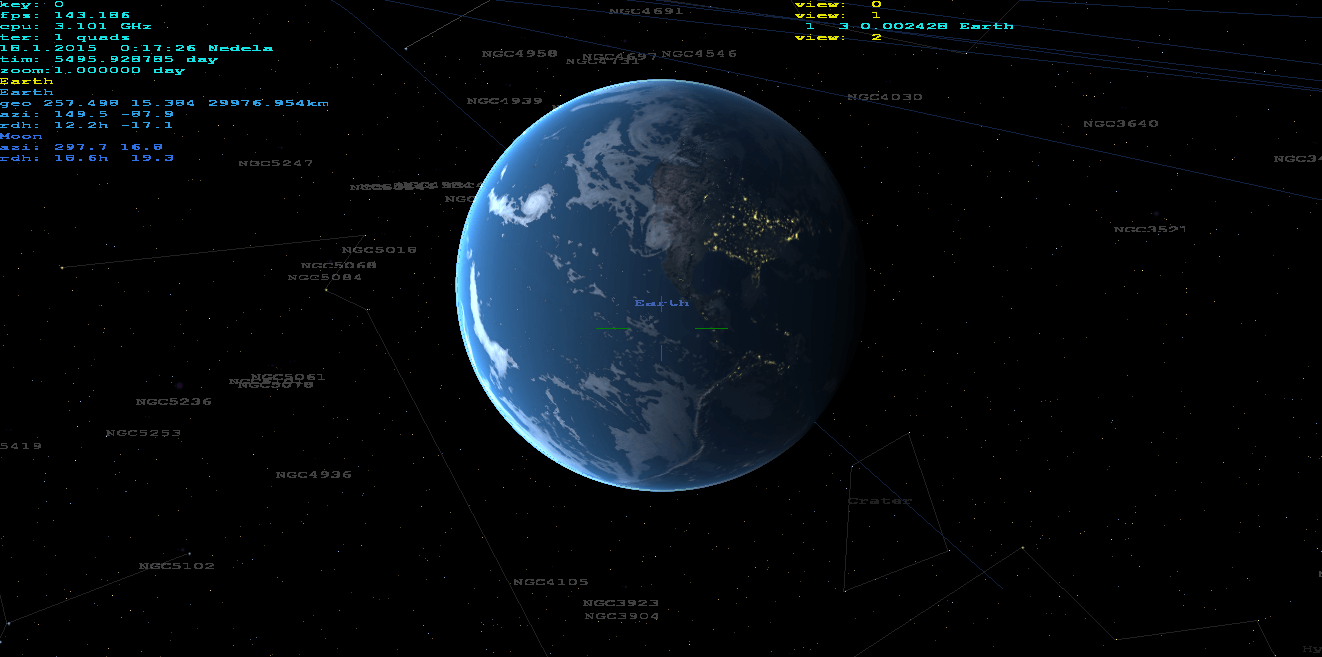
   Как вы можете видеть, он отлично работает на любой высоте или масштабировании, атмосфера сделана как этот шейдер рассеяния атмосферы.

2. моделирование

   Я не использую гравитационное моделирование n-тела, потому что для этого вам нужно много данных, которые очень очень трудно получить (и практически невозможно с желаемой точностью). Расчеты должны быть сделаны очень точно.

   Вместо этого я использую уравнение Кеплера, чтобы увидеть это:

   • Решение уравнения Кеплера
   • Реализация C++.

   Если вы все еще хотите использовать гравитационную модель, используйте горизонты JPL от NASA. Я думаю, что у них есть также исходные коды на C/C++, но они используют несовместимую систему ссылок с моими картами, поэтому она непригодна для меня.

   В общем случае уравнение Кеплера имеет большую ошибку, но со временем оно не увеличивается слишком сильно. Гравитационная модель более точна, но ее ошибка возрастает со временем, и вам необходимо постоянно обновлять данные астрономического тела, чтобы она работала...

[edit1] точность интеграции

Ваша текущая реализация выглядит так:

// object variables
double  acc[3],vel[3],pos[3];
// timer iteration
double dt=timer.interval;
for (int i=0;i<3;i++)
 {
 vel[i]+=acc[i]*dt;
 pos[i]+=vel[i]*dt;
 }

Проблема в том, что если вы добавляете очень маленькое и очень большое значение, то перед добавлением они сдвигаются к одному и тому же показателю степени, что округляет значимые данные. Чтобы избежать этого, просто замените его следующим

// object variables
double          vel0[3],pos0[3]; // low
double          vel1[3],pos1[3]; // high
double  acc [3],vel [3],pos [3]; // full
// timer iteration
double dt =timer.interval;
double max=10.0; // precision range constant
for (int i=0;i<3;i++)
 {
 vel0[i]+=acc[i]*dt; if (fabs(vel0[i]>=max)) { vel1[i]+=vel0[i]; vel0[i]=0.0; } vel[i]=vel0[i]+vel1[i];
 pos0[i]+=vel[i]*dt; if (fabs(pos0[i]>=max)) { pos1[i]+=pos0[i]; pos0[i]=0.0; } pos[i]=pos0[i]+pos1[i];
 }

Сейчас xxx0 интегрирован до max and the whole thing is added to xxx1

The rounding is still there but it is not cumulative anymore. Вы должны выбрать max value that the integration itself is safe and also the addition xxx0+xxx1 have to be safe. So if the numbers are too different for one spliting then split twice or more ...

• лайк: xxx0+=yyy*dt; if (fabs(xxx0>max0))... if (fabs(xxx1>max1))...

[Edit2] Stars

• The Colors of the Stars The best star visualization I ever saw
• Star BV color index to apparent RGB color all star catalogues uses BV index
• Using Stelar catalogs also star names cross-reference link is there
• Skybox: combine different star data

[Edit3] Improving Newton d'Lambert integration precision even more

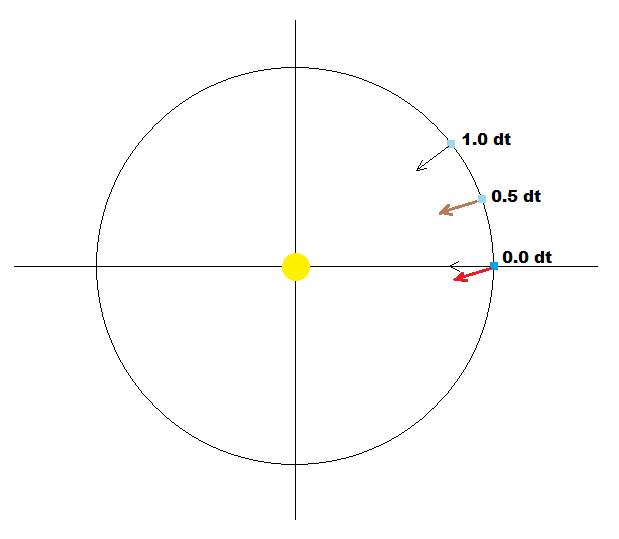
The basic problem with iterative integration is that applaying gravity based acceleration based on current body position will result in bigger orbits because durring integration step dt the position changes a bit which is not accounted in the naive integration. To remedy this take a look at this picture:

Let assume our body is at circular orbit and in the 0 deg position. Instead of using acceleration direction based on current position I used position after 0.5*dt, This augment the acceleration small bit resulting in much much higher precision (correspondence to Kepler orbits). With this tweak I was able to successfully convert from Kepler orbit into Newton d'Lambert for 2 body system. (doing this for n-body is the next step). Of coarse correlating with real data from our solar system is only possible for 2 body system not affected by tidal effects and or moons. To construct own fictional data you can use Kepler circular orbit and contripedal force equalizing gravity:

G = 6.67384e-11;
v = sqrt(G*M/a);                           // orbital speed
T = sqrt((4.0*M_PI*M_PI*a*a*a)/(G*(m+M))); // orbital period

где a is the circular orbit radius m is body mass, M is focal body mass (sun). To maintain precision in acceptable tolerance (for me) the integration step dt должно быть:

dt = 0.000001*T

So to put new body for testing just put it at:

pos = (a,0,0)
vel = (0,sqrt(G*M/a),0)

While main focal body (Sun) is at:

pos = (0,0,0)
vel = (0,0,0)

This will place your body in circular orbit so you can compare Kepler versus Newton d'Lambert to evaluate precision of your simulation.

Answer 2

Как вы обнаружили, уменьшение масштабов не обязательно поможет. Вот некоторые полезные сведения, которые следует учитывать при использовании чисел с плавающей запятой: http://docs.oracle.com/cd/E19957-01/806-3568/ncg_goldberg.html

По сути, симуляция из первых принципов (законов Ньютона) плохо влияет на числовую точность, потому что вы не наделяете численные методы представлением о шкале важных эффектов, поэтому вы в конечном итоге выбрасываете целую кучу разных эффектов в разных масштабах. вместе и в результате низкая точность.

Обычно такие вещи, как эфемериды для планет, спутников и т. Д., Не начинаются с закона Ньютона. Они начинают с предположения, что орбиты являются кеплеровыми, а затем и с небольшими возмущающими поправками.

Вот алгоритм, который вычисляет положение планет (полуэмперически). http://ssd.jpl.nasa.gov/txt/aprx_pos_planets.pdf

Если вы хотите провести симуляцию N-тела, вам, похоже, потребуется больше точности. Если единица не позволяет использовать двойную точность, тогда я предлагаю выполнить вычисления в простом C#, а затем выполнить преобразование с одинарной точностью, когда работа будет выполнена.