Рассчитать время, когда солнце находится на X градусов ниже / выше горизонта
Я хочу знать, в какое время солнце находится на X градусов ниже / выше горизонта.
Например, я хочу найти время, когда Солнце находится на 19,75 градуса ниже горизонта. Я думаю, что это как-то связано с зенитом в функции date_sunrise/date_sunset но я не уверен.
Заранее спасибо!
1 ответ
собрать данные эфемерид Солнца за день, который вам нужен
сделайте шаги за 1 час и получите положение Солнца в азимутальных координатах для нужного вам географического положения. Либо используйте уравнения, которые вы нашли, либо используйте какой-либо веб-сервис, например:
- JPL Horizons не нравится этот, поскольку они используют странные выходные системы отсчета, которые не соответствуют моим измерениям, но, скорее всего, я что-то преобразую по пути...
Обсерватория Прешова - это мой любимый (но на словацком) вывод, который легко копируется в двигатели шахты, а вывод соответствует наблюдениям, вычислениям, оценкам и измерениям шахты. Просто заполните:
- географическое положение (Miesto pozorovania)
- дата, время (дата рождения)
- внизу слева: интервал [дни], шаг интервала [дни]
- нажмите на кнопку для Солнца (Slnko), Луны (Mesiac), Планет (Planety)
Есть много таких страниц, просто посмотрите, но всегда проверяйте, выводят ли они правильные данные. Я использую законы / уравнения Кеплера, формирующие движения планет (более низкая точность, но для Земли-Солнца должна быть в порядке). В настоящее время двигатели используют гравитационную модель (но это нестабильно с более длительными периодами времени)
обрабатывать данные как набор трехмерных точек вдоль полилинии (азимут, высота, время)
сейчас просто найди в данных 2 балла
один ниже желаемого угла и следующий выше желаемого угла. Точки стенда должны быть соседними. Если какая-либо точка находится под нужным углом, значит, у вас уже есть решение, так что остановитесь
интерполировать время пересечения угла высоты
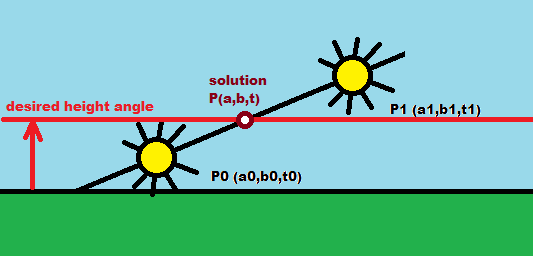
так что если желаемый угол высоты
bи хотел времяtзатем:a0,a1азимутальные углыb0,b1углы высотыt0,t1времена
тогда просто решите эту линейную систему:
b=b0+(b1-b0)*u t=t0+(t1-t0)*uтак что если я не совершил какую-нибудь глупую ошибку
t=t0+((t1-t0)*(b-b0)/(b1-b0))
[Заметки]
если вам не нужна слишком высокая точность (и использование выше 100 годы), и географическое положение будет фиксированным, тогда вы можете составить таблицу за весь год и периодически использовать эти данные. Таким образом, вам не понадобится шаг 1 во время выполнения.
[Edit1] закон Кеплера
если вы хотите пойти по этому пути, посмотрите здесь. Вам понадобятся параметры орбиты и вращения Земли. Они извлечены из эфемеридного двигателя шахты *.ini для солнечной системы:
[Earth]
txr_map=Earth_Map.jpg
txr_nor=Earth_Normal.jpg
txr_clouds=Earth_Cloud.jpg
txr_lights=Earth_Light.jpg
txr_ring_map=
txr_ring_alpha=
is_star=0
mother=Sun
re=6378141.2
rp=6356754.79506139
r0=-1
r1=-1
ha=60000
vd=250000
B0r=0.1981
B0g=0.4656
B0b=0.8625
B0a=0.75
t0=-0.0833333333333333 ; this means 1.1.2000 00:00:00 UT
a=149597896927.617
da=-0.122872993839836
e=0.01673163
de=-1.00232717316906E-9
i=-9.48516635288838E-6
di=-6.38963964003634E-9
O=-0.004695
dO=-1.15274665428334E-7
o=1.79646842620403
do=1.51932094052745E-7
M =1.7464
dM =0.0172021242603194
ddM=0
rota0 =3.0707963267949
rotda =6.30038738085328
prea0 =1.5707963267949
preda =-6.68704522111755E-7
prei =0.409124584728753
predi =0
nuta =0
nutda =0
nutia =0
nutdia=0
nutii =0
nutdii=0
и вот объяснения:
[Name] [string id] object ID name
txr_map [filename] surface texture
txr_nor [filename] surface normal/bump texture
txr_clouds [filename] cloud blend texture (white cloud, black clear sky)
txr_lights [filename] night surface texture
txr_ring_map [filename] rings color texture
txr_ring_alpha [filename] rings alpha texture (alpha0 transparent, alpha1 solid)
is_star [0/1] is star ?
mother [string] "" or owner object name
re [m] equator radius
rp [m] polar radius
r0 [m] -1 or rings inner radius
r1 [m] -1 or rings outer radius
ha [m] 0 or atmosphere thickness
vd [m] -1 or atmosphere view depth
B0r <0,1> star R light or atmosphere color
B0g <0,1> star G light or atmosphere color
B0b <0,1> star B light or atmosphere color
B0a <0,1> overglow of star below horizont
t0 [day] t0 time the parameters are taken after 1.1.2000 00:00:00
a [m] a main semiaxis
da [m/day] a change in time
e [-] e eccentricity
de [-/day] e change in time
i [rad] i inclination
di [rad/day] i change in time
O [rad] O (node n) position of inclination axis
dO [rad/day] O node shift (pi2/T)
o [rad] o perihelium (no change in inclination position)
do [rad/day] o perihelium shift (pi2/T)
M [rad] M rotation around owner position in t0
dM [rad/day] dM orbital rotation (pi2/draconic month)
ddM0 [rad/day^2] dM change in time
rota0 [rad] rota0 rotation around self axis position in t0
rotda [rad/day] rotda mean rotation around self axis
prea0 [rad] prea rotation axis position in t0
preda [rad/day] preda precession rotation (pi2/Platonic year)
prei [rad] prei equator inclination to ecliptic
predi [rad/day] prei change in time
nuta [rad] nuta angle position on nutation ellipse
nutda [rad/day] nutation rotation (pi2/T)
nutia [rad] nutia nutation (of rotation axis) ellipse semiaxis axis in ecliptic plane
nutdia [rad/day] nutia change in time
nutii [rad] nutii nutation (of rotation axis) ellipse semiaxis axis in rotation axis direction
nutdii [rad/day] nutii change in time
Игнорируйте is_star, текстуры, кольца и параметры атмосферы. Так:
- получить Солнце в положение
(0,0,0)в декартовых координатах вычислить положение Земли
(x,y,z)из закона КеплераСолнце тогда
(-x,-y,-z)в геоцентрических координатахповернуть назад путем ежедневного вращения, прецессии, нутации
(-x,-y,-z) -> (x',y',z')- вычисление
NEHрамка для вашей геолокации(North,East,High(Up)) - перерабатывать
(x',y',z')в NEH местные координаты(xx,yy,zz) вычислить:
azimut=atanxy(-xx,-yy) height=atanxy(sqrt((xx*xx)+(yy*yy)),-zz)и это все
Вот мое гелиоцентрическое вычисление положения астро тела:
void astro_body::compute(double t)
{
// t is time in days after 1.1.2000 00:00:00
// double pos[3] is output heliocentric position [m]
// reper rep is output heliocentric position [m] and orientation transform matrix (mine class) where Z is rotation axis (North pole) and X is long=0,lat=0
rot_a.compute(t); // compute actual value for orbital parameters changing in time
pre_a.compute(t); // the actual parameter is in XXX.a you can ignore this part
pre_i.compute(t);
nut_a.compute(t);
nut_ia.compute(t);
nut_ii.compute(t);
// pre_a=pre_a0+(pre_da.a*dt)+(nut_ia*cos(nut_a)); // some old legacy dead code
// pre_i=pre_i0+(pre_di.a*sin(pre_e))+(nut_ii*sin(nut_a));
rep.reset(); // rep is the transform matrix representing body coordinate system (orientation and position)
rep.lrotz(pre_a.a); // local rotation around reps Z axis by pre_a.a [rad] angle
rep.lroty(pre_i.a);
rep.lrotx(nut_ia.a*cos(nut_a.a));
rep.lroty(nut_ii.a*sin(nut_a.a));
rep.lrotz(rot_a.a);
a.compute(t); // the same as above can ignore this part
e.compute(t);
i.compute(t);
O.compute(t);
o.compute(t);
M.compute(t);
M.compute(t);
double c0,c1,c2,sO,si,cO,ci,b; // trajectory constants
double x,y;
int q;
if (e.a>=1.0) e.a=0;
c0=sqrt((1.0-e.a)/(1.0+e.a)); // some helper constants computation
c1=sqrt((1.0+e.a)/(1.0-e.a));
c2=a.a*(1-e.a*e.a);
sO=sin(O.a);
cO=cos(O.a);
si=sin(-i.a);
ci=cos(-i.a);
b=a.a*sqrt(1.0-e.a);
M.a-=o.a; // correction
M.a=M.a-pi2*floor(M.a/pi2);
E=M.a;
for (q=0;q<20;q++) E=M.a+e.a*sin(E); // Kepler's equation
V=2.0*atan(c1*tan(E/2.0));
r=c2/(1.0+e.a*cos(V));
pos[0]=r*cos(V+o.a-O.a); // now just compute heliocentric position along ecliptic ellipse
pos[1]=r*sin(V+o.a-O.a); // and then rotate by inclination
pos[2]=-pos[1]*si;
pos[1]=+pos[1]*ci;
x=pos[0]; y=pos[1];
pos[0]=x*cO-y*sO;
pos[1]=x*sO+y*cO;
if ((mother>=0)&&(tab!=NULL)) vector_add(pos,pos,tab[mother].pos); // if satelite like Moon add owners position
rep.gpos_set(pos); // set the global position to transform matrix also
}
//---------------------------------------------------------------------------
reper класс довольно сложный (что-то вроде GLM), единственное, что вам нужно от него - это локальные ротации (все остальное - базовое). вот как lrotx работает:
double c=cos(ang),s=sin(ang);
double rot[16],inv[16]; // rot is the rotation around x transform matrix
rot=(1, 0, 0, 0,
0, c,-s, 0,
0, s, c, 0,
0, 0, 0, 1);
inv=inverse(rep); // inverse is inverse matrix 4x4
inv=inv*rot
rep=inverse(inv);
repматрица ввода и выводаangугол поворота [рад]
теперь вы можете использовать респ для преобразования в / из локальной системы координат Земли
- LCS to GCS
(l2g) ... (gx,gy,gz)=rep*(lx,ly,lz) - GCS для LCS
(g2l) ... (lx,ly,lz)=inverse(rep)*(gx,gy,gz)
локальной является система координат Земли и глобальная система координат Солнца