Как нарисовать карту неба?

Question

Как мне нарисовать звездную карту, как это?

Я имею:

1. Звездная база данных с координатами (прямое восхождение и склонение)
2. Координаты наблюдателя (широта, долгота)
3. Время наблюдения

Мне нужна формула, которая учитывала эти параметры.

Answer 1

1. звездная база данных

   Google для:

   • BSC (каталог ярких звезд) ~10K звезд до +6,5 мАг (невооруженным глазом)
   • Hipparcos ~ 118K звезд до +12 мАг (телескопы), а также имеет параллакс (3D-координаты) и многое другое
   • Гиппаркос мой любимый. оба могут быть свободно загружены в формате ASCII со многих серверов Astornomy просто Google...

2. планеты (тела)

   Вы можете собрать параметры орбиты, необходимые из многих сайтов. Вам понадобятся все эти элементы Orbital_elements, например, вот некоторые

3. симуляция (вычислить позицию во времени)

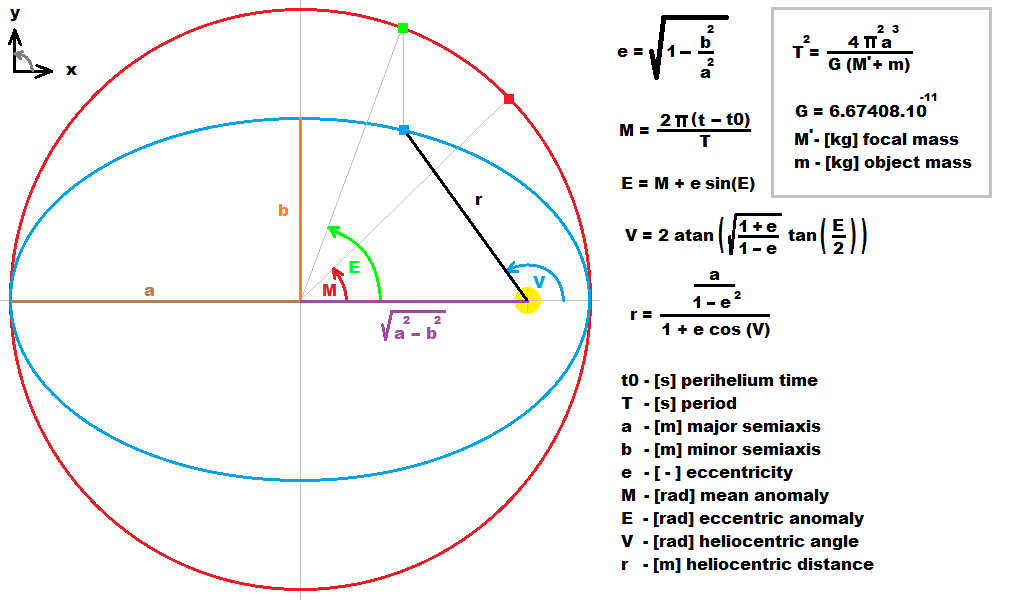
   Для планет это просто получение эфемерид планет / спутников, что можно сделать путем вычисления уравнения Кеплера

   M=E-e*sin(E)
   

   где:

   
   M средний угол (как будто планета имеет круговую траекторию и постоянную скорость)
   E реальный угол от центра эллипса (с учетом закона Кеплера)

   Вы можете решить это так:

   for (E=M,q=0;q<20;q++) E=M+e*sin(E);
   

   Теперь ты знаешь E для любого M что все, что вам нужно Просто рассчитайте положение на эллипсе и поверните его по наклону. M вычисляется также просто вам нужно знать время t0 когда планета пересекает угол 0. Тогда:

   M = (t-t0) * dM
   

   где dM вращение вокруг Солнца Если время в днях, то dM в [rad/day], Для Земли это 2.0*pi/tropical_year, Это приведет вас ко всем глобальным позициям планет (относительно Солнца)

   

   Для получения дополнительной информации смотрите здесь Как рассчитать планетарные позиции

4. Вид Земли

   Экваториальные координаты относятся к Земле, поэтому вам нужно добавить ежедневное вращение Земли в симуляцию. Просто создайте матрицу преобразования с одной осью, повернутой на 23.5 deg в "правильном" направлении и добавьте вращение по этой оси. Также добавьте вращение в ваше географическое положение. После этого переведите эту матрицу в вычисленное положение Земли. Отсюда легко преобразовать все глобальные координаты в вид вашей Земли, чтобы вы могли теперь вывести данные на изображение или на экран.

[Заметки]

Будьте осторожны, какой период вращения вы используете!!!

• Земли tropical_year = 365.242195601852 days
• Вращение дня Земли dM = 0.0172021242603194 rad/day

• день означает солнечный день!!! как юлианское свидание...

  Всегда калибруйте свои данные с помощью другого программного обеспечения или реальной вещи. Есть некоторые библиотеки, которые делают все это только в Google. Для повышения точности реализации нутации параметры прецессии и орбиты меняются со временем.

[Edit1] простой пример C++

Я упростил полный пример C++, так что только a,b,M используются.

//---------------------------------------------------------------------------
void ellipse_kepler(double &x,double &y,double a,double b,double M)
    {
    int q;
    double c1,c2,e,E,V,r;
    e=1.0-((b*b)/(a*a));                // eccentricity
    if (e>=1.0) e=0;                    // wrong e
    c1=sqrt((1.0+e)/(1.0-e));           // some helper constants computation
    c2=a*(1-e*e);
    //b=a*sqrt(1.0-e);
    for (E=M,q=0;q<20;q++) E=M+e*sin(E);// Kepler's equation
    V=2.0*atan(c1*tan(E/2.0));
    r=c2/(1.0+e*cos(V));
    x=r*cos(V);                         // heliocentric ellipse
    y=r*sin(V);
    }
//---------------------------------------------------------------------------
void draw()
    {
    scr.cls(clBlack);
    double x0,y0,x,y,a,b,M,r=5;

    // ellipse
    x0=scr.xs>>1;
    y0=scr.ys>>1;
    a=(x0*75)/100;
    b=(y0*35)/100;
    x0+=1.5*(a-b);
    scr.bmp->Canvas->Pen->Color=clAqua;
    for (M=0.0;M<=2.0*M_PI;M+=M_PI*0.01) // small step so the ellipse trajectory is not edgy
        {
        ellipse_kepler(x,y,a,b,M);
        x+=x0; y+=y0;
        if (M<=1e-10) scr.bmp->Canvas->MoveTo(x,y);
         else         scr.bmp->Canvas->LineTo(x,y);
        }
    scr.bmp->Canvas->Pen->Color=clAqua;
    scr.bmp->Canvas->Brush->Color=clYellow;
    scr.bmp->Canvas->Ellipse(x0-r,y0-r,x0+r,y0+r);
    scr.bmp->Canvas->Brush->Color=clBlue;
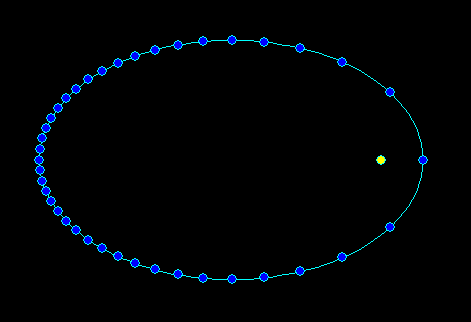
    for (M=0.0;M<=2.0*M_PI;M+=M_PI*0.05) // constant time step for the dots a bit bigger so not many dots are on one place
        {
        ellipse_kepler(x,y,a,b,M);
        x+=x0; y+=y0;
        scr.bmp->Canvas->Ellipse(x-r,y-r,x+r,y+r);
        }
    scr.rfs();
    }
//---------------------------------------------------------------------------

Первая функция вычисляет 2D позицию (x,y) на кеплеровской гелиоцентрической траектории в то время как a>=b полуоси и M средний угол (линейный угол как время, масштабированное до <0,2*Pi> за год революции). Вторая функция просто визуализирует эллипс с помощью VCL/GDI, поэтому понятно, как использовать первую с постоянным шагом по времени, чтобы ее можно было увидеть вблизи перигелии, когда планета движется быстрее...