Аппроксимирующие данные с многосегментной кубической кривой Безье и расстоянием, а также с ограничением кривизны

Question

У меня есть некоторые географические данные (на рисунке ниже показаны пути реки в виде красных точек), которые я хочу аппроксимировать, используя многосегментную кубическую кривую Безье. С помощью других вопросов о стековом потоке здесь и здесь я нашел алгоритм Филипа Дж. Шнайдера из "Graphics Gems". Я успешно реализовал это и могу сообщить, что даже с тысячами пунктов это очень быстро. К сожалению, эта скорость имеет некоторые недостатки, а именно то, что подгонка выполняется довольно небрежно. Рассмотрим следующий рисунок:

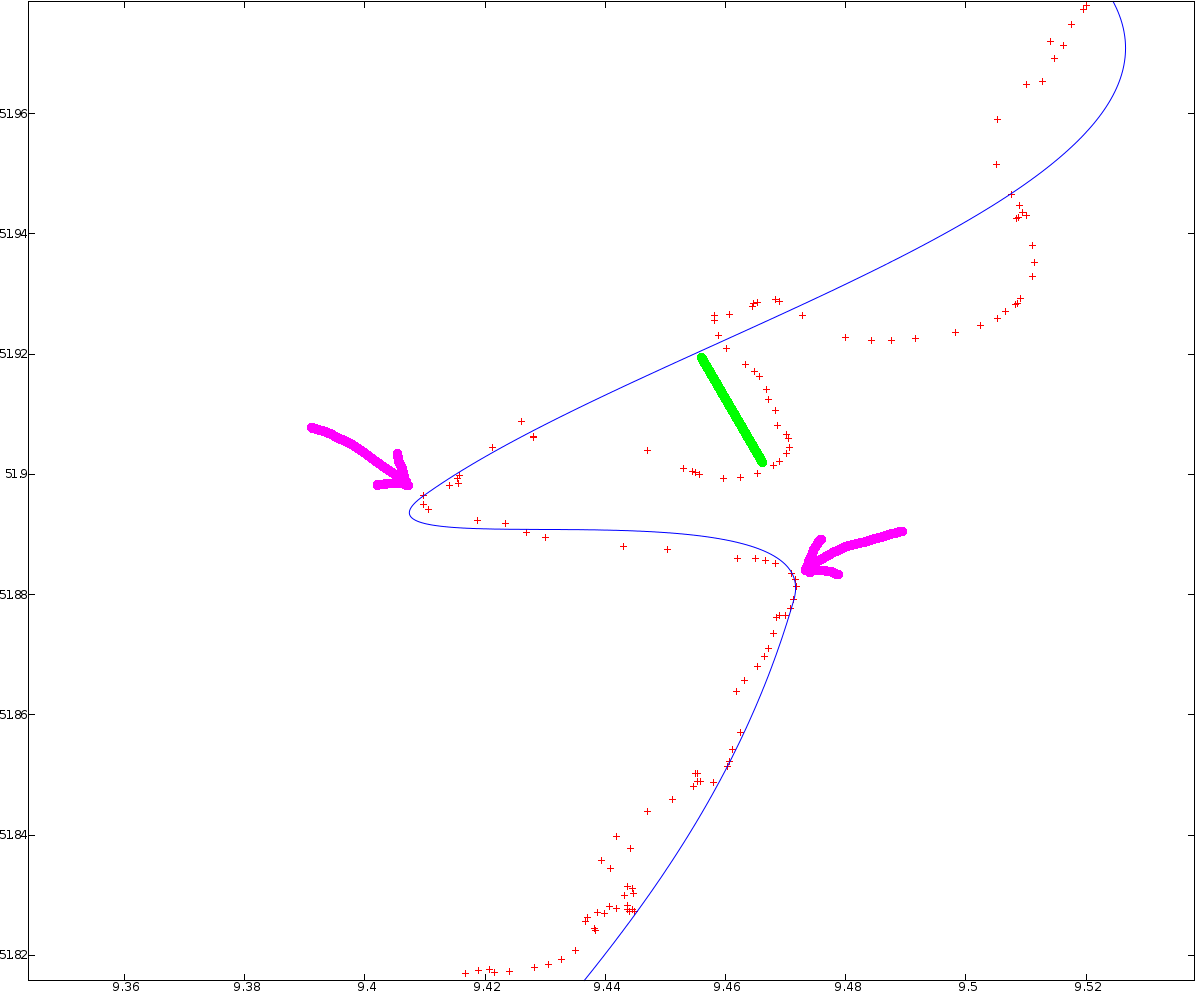
Красные точки - мои исходные данные, а синяя линия - многосегментный Безье, созданный алгоритмом Шнайдера. Как вы можете видеть, вход в алгоритм был допуск, который по крайней мере так же высоко, как указывает зеленая линия. Тем не менее, алгоритм создает кривую Безье, которая имеет слишком много крутых поворотов. Вы также видите эти ненужные резкие повороты на изображении. Легко представить кривую Безье с менее резкими поворотами для показанных данных, сохраняя при этом условие максимального допуска (просто слегка сдвиньте кривую Безье в направлении пурпурных стрелок). Кажется, проблема в том, что алгоритм выбирает точки данных из моих исходных данных в качестве конечных точек отдельных кривых Безье (точки пурпурных стрелок указывают на некоторых подозреваемых). С такими ограниченными конечными точками кривых Безье становится ясно, что алгоритм иногда дает довольно резкие изгибы.

Что я ищу, так это алгоритм, который аппроксимирует мои данные с помощью многосегментной кривой Безье с двумя ограничениями:

• многосегментная кривая Безье никогда не должна находиться более чем на определенном расстоянии от точек данных (это предусмотрено алгоритмом Шнайдера)
• многосегментная кривая Безье никогда не должна создавать слишком острые изгибы. Один из способов проверки этого критерия состоит в том, чтобы накатить круг с минимальным радиусом кривизны вдоль кривой Безье, состоящей из нескольких сегментов, и проверить, касается ли он всех частей кривой на своем пути. Хотя кажется, что есть лучший метод, включающий перекрестное произведение первой и второй производной

Решения, которые я нашел, которые создают лучшие соответствия, к сожалению, либо работают только для одиночных кривых Безье (и опускают вопрос о том, как найти хорошие начальные и конечные точки для каждой кривой Безье в многосегментной кривой Безье), либо не допускают минимального ограничения кривизны. Я чувствую, что минимальное ограничение кривизны является сложным условием.

Вот еще один пример (это нарисовано от руки и не на 100% точно):

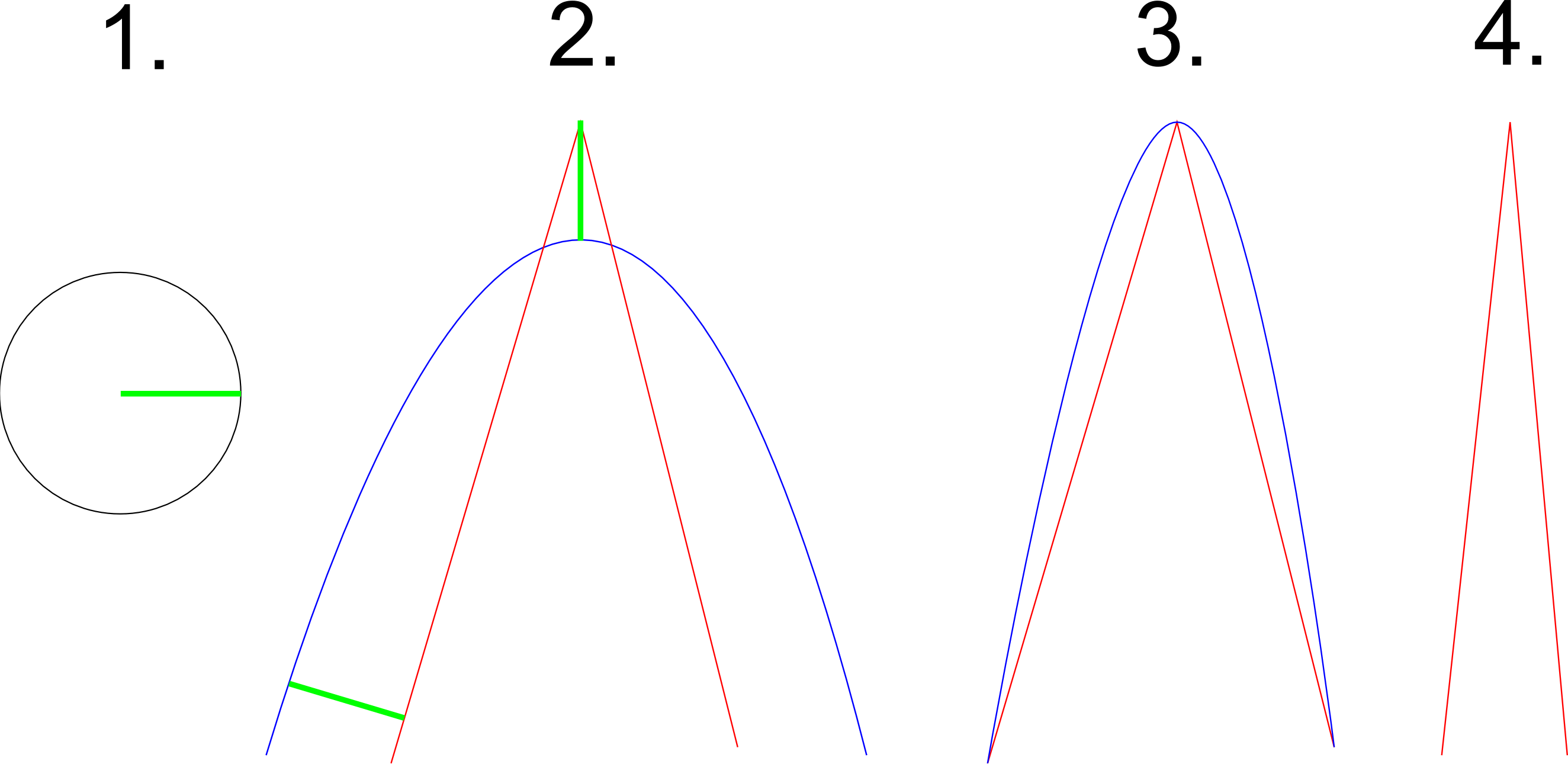
Предположим, что на рисунке 1 показаны как ограничение кривизны (круг должен соответствовать всей кривой), так и максимальное расстояние любой точки данных от кривой (которая является радиусом зеленого круга). Успешное приближение красного пути на рисунке 2 показано синим цветом. Это приближение учитывает условие кривизны (круг может вращаться внутри всей кривой и касается ее везде), а также условие расстояния (показано зеленым). На рисунке три показано другое приближение к пути. Хотя он учитывает условие расстояния, ясно, что круг больше не вписывается в кривизну. На рисунке 4 показан путь, который невозможно аппроксимировать с заданными ограничениями, потому что он слишком заостренный. Предполагается, что этот пример иллюстрирует, что для правильной аппроксимации некоторых заостренных поворотов на пути необходимо, чтобы алгоритм выбирал контрольные точки, которые не являются частью пути. На рисунке три показано, что если были выбраны контрольные точки вдоль пути, ограничение кривизны больше не может быть выполнено. Этот пример также показывает, что алгоритм должен выходить из некоторых входных данных, поскольку его невозможно аппроксимировать с заданными ограничениями.

Существует ли решение этой проблемы? Решение не должно быть быстрым. Если для обработки 1000 баллов требуется день, то это нормально. Решение также не обязательно должно быть оптимальным в том смысле, что оно должно привести к подгонке наименьших квадратов.

В конце я реализую это на C и Python, но я могу читать и большинство других языков.

Answer 1

Я нашел решение, которое выполняет мой критерий. Решение состоит в том, чтобы сначала найти B-сплайн, который аппроксимирует точки в смысле наименьших квадратов, а затем преобразовать этот сплайн в многосегментную кривую Безье. Преимущество B-сплайнов состоит в том, что, в отличие от кривых Безье, они не будут проходить через контрольные точки, а также предоставят способ указать желаемую "плавность" кривой аппроксимации. Необходимая функциональность для генерации такого сплайна реализована в библиотеке FITPACK, к которой scipy предлагает привязку Python. Предположим, я прочитал свои данные в списках x а также yтогда я могу сделать:

import matplotlib.pyplot as plt
import numpy as np
from scipy import interpolate
tck,u = interpolate.splprep([x,y],s=3)
unew = np.arange(0,1.01,0.01)
out = interpolate.splev(unew,tck)
plt.figure()
plt.plot(x,y,out[0],out[1])
plt.show()

Результат тогда выглядит так:

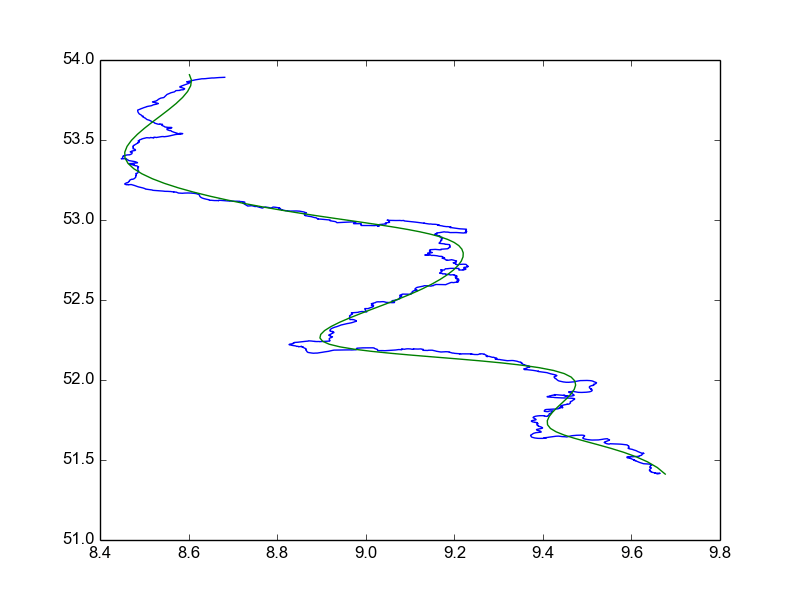
Если я хочу, чтобы кривая была более гладкой, то я могу увеличить s параметр для splprep, Если я хочу приближение ближе к данным, я могу уменьшить s параметр для меньшей плавности. Проходя через несколько s Параметры программно я могу найти хороший параметр, который соответствует данным требованиям.

Вопрос в том, как преобразовать этот результат в кривую Безье. Ответ в этом письме Захари Пинкус. Я повторю его решение здесь, чтобы дать полный ответ на мой вопрос:

def b_spline_to_bezier_series(tck, per = False):
  """Convert a parametric b-spline into a sequence of Bezier curves of the same degree.

  Inputs:
    tck : (t,c,k) tuple of b-spline knots, coefficients, and degree returned by splprep.
    per : if tck was created as a periodic spline, per *must* be true, else per *must* be false.

  Output:
    A list of Bezier curves of degree k that is equivalent to the input spline. 
    Each Bezier curve is an array of shape (k+1,d) where d is the dimension of the
    space; thus the curve includes the starting point, the k-1 internal control 
    points, and the endpoint, where each point is of d dimensions.
  """
  from fitpack import insert
  from numpy import asarray, unique, split, sum
  t,c,k = tck
  t = asarray(t)
  try:
    c[0][0]
  except:
    # I can't figure out a simple way to convert nonparametric splines to 
    # parametric splines. Oh well.
    raise TypeError("Only parametric b-splines are supported.")
  new_tck = tck
  if per:
    # ignore the leading and trailing k knots that exist to enforce periodicity 
    knots_to_consider = unique(t[k:-k])
  else:
    # the first and last k+1 knots are identical in the non-periodic case, so
    # no need to consider them when increasing the knot multiplicities below
    knots_to_consider = unique(t[k+1:-k-1])
  # For each unique knot, bring it's multiplicity up to the next multiple of k+1
  # This removes all continuity constraints between each of the original knots, 
  # creating a set of independent Bezier curves.
  desired_multiplicity = k+1
  for x in knots_to_consider:
    current_multiplicity = sum(t == x)
    remainder = current_multiplicity%desired_multiplicity
    if remainder != 0:
      # add enough knots to bring the current multiplicity up to the desired multiplicity
      number_to_insert = desired_multiplicity - remainder
      new_tck = insert(x, new_tck, number_to_insert, per)
  tt,cc,kk = new_tck
  # strip off the last k+1 knots, as they are redundant after knot insertion
  bezier_points = numpy.transpose(cc)[:-desired_multiplicity]
  if per:
    # again, ignore the leading and trailing k knots
    bezier_points = bezier_points[k:-k]
  # group the points into the desired bezier curves
  return split(bezier_points, len(bezier_points) / desired_multiplicity, axis = 0)

Так что B-Splines, FITPACK, numpy и scipy спасли мой день:)

Answer 2

1. полигонизировать данные

   найдите порядок точек, чтобы вы просто находили ближайшие точки друг к другу и пытались их соединить "линиями". Избегайте возврата к исходной точке

2. вычислить вывод по пути

   это изменение направления "линий", когда вы нажимаете локальную мин. или макс. там находится ваша контрольная точка... Делайте это, чтобы уменьшить ваши входные данные (оставьте только контрольные точки).

3. кривая

   Теперь используйте эти точки в качестве контрольных точек. Я настоятельно рекомендую интерполяционный полином для обоих x а также y отдельно например как то так:

   x=a0+a1*t+a2*t*t+a3*t*t*t
   y=b0+b1*t+b2*t*t+b3*t*t*t
   

   где a0..a3 вычисляются так:

   d1=0.5*(p2.x-p0.x);
   d2=0.5*(p3.x-p1.x);
   a0=p1.x;
   a1=d1;
   a2=(3.0*(p2.x-p1.x))-(2.0*d1)-d2;
   a3=d1+d2+(2.0*(-p2.x+p1.x));
   

   • b0 .. b3 вычисляются таким же образом, но используют координаты у конечно
   • p0..p3 контрольные точки для кубической кривой интерполяции
   • t =<0.0,1.0> параметр кривой от p1 в p2

   это гарантирует, что позиция и первая деривация являются непрерывными (c1), а также вы можете использовать BEZIER, но это не будет так хорошо, как это.

[edit1] слишком острые края - большая проблема

Чтобы решить эту проблему, вы можете удалить точки из своего набора данных до получения контрольных точек. Я могу придумать два способа сделать это прямо сейчас... выбрать, что лучше для вас

1. удалить точки из набора данных при слишком высоком первом выводе

   dx/dl или же dy/dl где x,y координаты и l длина кривой (вдоль ее пути). Точное вычисление радиуса кривизны из вывода кривой сложно

2. удалить точки из набора данных, которые приводят к слишком малому радиусу кривизны

   вычислить пересечение средней точки соседних отрезков (черных линий). Перпендикулярные оси, как на изображении (красные линии), расстояние до него и точка соединения (синяя линия) - это радиус вашей кривизны. Когда радиус кривизны меньше, ваш предел удалит эту точку...

   

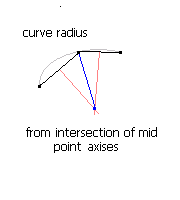
   Теперь, если вам действительно нужны только кубики BEZIER, вы можете преобразовать мою кубическую интерполяцию в кубик BEZIER следующим образом:

//  ---------------------------------------------------------------------------
//  x=cx[0]+(t*cx[1])+(tt*cx[2])+(ttt*cx[3]); // cubic x=f(t), t = <0,1>
//  ---------------------------------------------------------------------------
//  cubic matrix                           bz4 = it4
//  ---------------------------------------------------------------------------
//  cx[0]=                            (    x0) =                    (    X1)
//  cx[1]=                   (3.0*x1)-(3.0*x0) =           (0.5*X2)         -(0.5*X0)
//  cx[2]=          (3.0*x2)-(6.0*x1)+(3.0*x0) = -(0.5*X3)+(2.0*X2)-(2.5*X1)+(    X0)
//  cx[3]= (    x3)-(3.0*x2)+(3.0*x1)-(    x0) =  (0.5*X3)-(1.5*X2)+(1.5*X1)-(0.5*X0)
//  ---------------------------------------------------------------------------
    const double m=1.0/6.0;
    double x0,y0,x1,y1,x2,y2,x3,y3;
    x0 = X1;           y0 = Y1;
    x1 = X1-(X0-X2)*m; y1 = Y1-(Y0-Y2)*m;
    x2 = X2+(X1-X3)*m; y2 = Y2+(Y1-Y3)*m;
    x3 = X2;           y3 = Y2;

Если вам нужно обратное преобразование, смотрите:

• Кривая Безье с контрольными точками внутри кривой

Answer 3

Вопрос был опубликован давно, но вот простое решение, основанное на splprep, находящее минимальное значение s, позволяющее выполнить критерии минимального радиуса кривизны.

route — это набор входных точек, первое измерение — количество точек.

      import numpy as np
from scipy.interpolate import splprep, splev

#The minimum curvature radius we want to enforce
minCurvatureConstraint = 2000
#Relative tolerance on the radius
relTol = 1.e-6

#Initial values for bisection search, should bound the solution
s_0 = 0
minCurvature_0 = 0
s_1 = 100000000 #Should be high enough to produce curvature radius larger than constraint
s_1 *= 2
minCurvature_1 = np.float('inf')

while np.abs(minCurvature_0 - minCurvature_1)>minCurvatureConstraint*relTol:
    s = 0.5 * (s_0 + s_1)
    tck, u  = splprep(np.transpose(route), s=s)
    smoothed_route = splev(u, tck)
    
    #Compute radius of curvature
    derivative1 = splev(u, tck, der=1)
    derivative2 = splev(u, tck, der=2) 
    xprim = derivative1[0]
    xprimprim = derivative2[0]
    yprim = derivative1[1]
    yprimprim = derivative2[1]
    curvature = 1.0 / np.abs((xprim*yprimprim - yprim* xprimprim) / np.power(xprim*xprim + yprim*yprim, 3 / 2))
    minCurvature = np.min(curvature)
    print("s is %g => Minimum curvature radius is %g"%(s,np.min(curvature)))

    #Perform bisection
    if minCurvature > minCurvatureConstraint:
        s_1 = s
        minCurvature_1 = minCurvature
    else:
        s_0 = s
        minCurvature_0 = minCurvature

Для поиска подходящего s_1 могут потребоваться некоторые уточнения, такие как итерации, но это работает.