Как определить кривизну кубического пути Безье в конечной точке

Question

Я работал над проектом, в котором я использую пути Безье, чтобы нарисовать нужные мне кривые. Каждая базовая фигура в моем проекте состоит из трех кубических кривых Безье, расположенных так, что склоны совпадают там, где они встречаются.

Основная проблема, которую мне нужно решить, состоит в том, пересекает ли составная кривая, составленная из трех кривых Безье, сама с собой. Подумав немного, я понял, что, учитывая ограничения кривых, я могу упростить задачу до чего-то другого:

Кривизна каждого из трех путей Безье должна быть противоположной в направлении кривизны относительно кривой, к которой она примыкает. Другими словами, должна быть точка перегиба, где одна кривая Безье граничит с другой. Если это не так, я хочу отклонить набор параметров, который сгенерировал кривые, и выбрать другой набор.

В любом случае, мой основной вопрос - как определить, существует ли точка перегиба, где кривые упираются друг в друга.

На иллюстрации каждая из трех кривых Безье показана другим цветом. Левая черная кривая изгибается в противоположном направлении от красной кривой в том месте, где они встречаются, а правая черная кривая - в том же направлении. Существует точка перегиба, где красная и левая черная кривая встречаются, но не там, где красная и правая черная кривая встречаются.

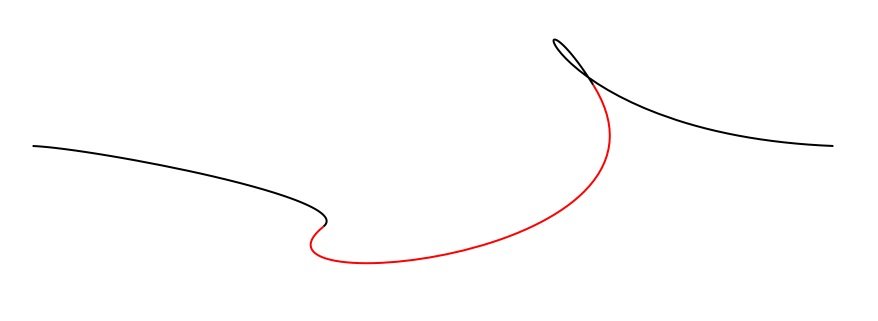
Изменить: ниже, я добавил еще одно изображение, показывающее многоугольник, включающий путь Безье. Линии пересечения многоугольника, показанные на черной кривой, проверяют точку перегиба, а не петлю. Я предполагаю, что одну кривую, пересекающую другую, можно проверить, проверив, пересекаются ли окружающие полигоны, как показано красной и синей кривыми.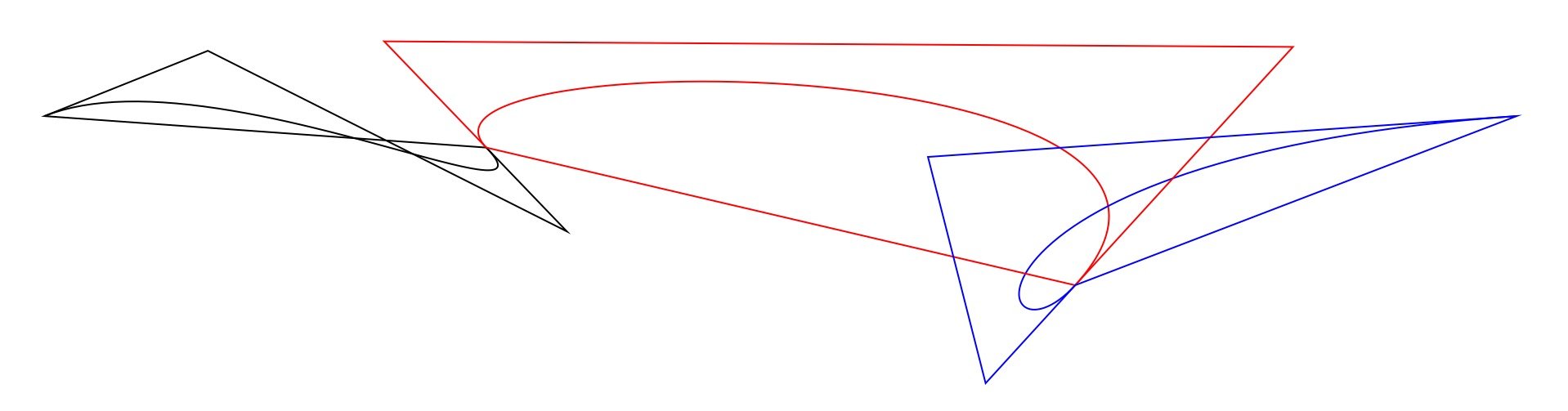

PS Поскольку возникли некоторые вопросы об ограничениях, я перечислю некоторые из них здесь:

• Самая левая точка и крайняя правая точка имеют одинаковое значение y.
• Значение x контрольной точки самой левой точки меньше
  значение x контрольной точки самой правой точки. Это держит
  черные и синие кривые пересекаются друг с другом.
• Наклон в крайней левой и правой точках находится в пределах +/- 10 градусов от горизонтали.
• Пересечение черной и красной кривых и пересечение красной и синей кривых делят полную кривую примерно на треть. У меня нет точных чисел, но примерная граница будет такой, что значение x левого конца красной кривой находится где-то между 25% и 40% от значения x самой правой точки.
• Значение y точек пересечения составляет +/- небольшую долю от общей ширины.
• Наклон на перекрестках составляет> 0,6 и< 3,0 (положительный или отрицательный).

Answer 1

Уравнение кривизны в меру простое. Вам нужен только знак кривизны, так что вы можете пропустить немного математики. Вас в основном интересует знак перекрестного произведения первой и второй производных.

Это упрощение работает только потому, что кривые соединяются плавно. Без равных касательных необходим более сложный тест.

Знак кривизны кривой Р:

ax = P[1].x - P[0].x;               //  a = P1 - P0
ay = P[1].y - P[0].y;
bx = P[2].x - P[1].x - ax;          //  b = P2 - P1 - a
by = P[2].y - P[1].y - ay;
cx = P[3].x - P[2].x - bx*2 - ax;   //  c = P3 - P2 - 2b - a
cy = P[3].y - P[2].y - by*2 - ay;

bc = bx*cy - cx*by;
ac = ax*cy - cx*ay;
ab = ax*by - bx*ay;

r = ab + ac*t + bc*t*t;

Обратите внимание, что r является перекрестным произведением первой и второй производных, а знак указывает направление кривизны. Вычислите r при t=1 на левой кривой и при t=0 на правой кривой. Если продукт отрицательный, то есть точка перегиба.

Если у вас есть кривые U, V и W, где U - левый черный, V - средний красный, а W - правый черный, то рассчитайте bc, ac и ab выше для каждого. Следующий тест будет верным, если оба соединения являются точками перегиба:

(Uab+Uac+Ubc)*(Vab) < 0 && (Vab+Vac+Vbc)*(Wab) < 0

У уравнения для кривизны есть знаменатель, который я проигнорировал. Он не влияет на знак кривизны и будет нулевым, если кривая была линией.

Математическое резюме:

// start with the classic bezier curve equation
P = (1-t)^3*P0 + 3*(1-t)^2*t*P1 + 3*(1-t)*t^2*P2 + t^3*P3
// convert to polynomial
P = P0 + 3*t*(P1 - P0) + 3*t^2*(P2 - 2*P1 + P0) + t^3*(P3 - 3*P2 + 3*P1 - P0)
// rename the terms to a,b,c
P = P0 + 3at + 3btt + cttt
// find the first and second derivatives
P' = 3a + 6bt + 3ctt
P" =      6b  + 6ct
// and the cross product after some reduction 
P' x P" = ab + act + bctt

Answer 2

Один из детерминированных способов проверить, имеет ли кривая Безье двойную точку или самопересечение, состоит в том, чтобы вычислить обратное уравнение и вычислить корень, поскольку уравнение инверсии кривой Безье всегда равно нулю в точке самопересечения. Как подробно описано в этом примере TWSederberg - заметки курса. Затем для определения того, пересекаются ли две кривые Безье (красный и черный в вопросе) друг с другом, есть несколько методов, двоичное подразделение (более простое в реализации) и отсечение Безье (очень хороший баланс эффективности и сложности кода), имплицитизация (не стоило того).

Но более эффективный способ сделать это, вероятно, состоит в том, чтобы разделить кривые на маленькие отрезки и найти пересечение. Вот один из способов сделать это. Особенно, когда вам интересно знать, пересекается ли путь сам, но не в точной точке пересечения.

Если у вас есть четко определенные предположения о расположении CV для кусочно-кривых Безье (или поли-Безье как @Pomax, упомянутый выше), вы можете попробовать метод, основанный на кривизне, как вы упомянули в своем вопросе.

Вот график кривизны на пути, аналогичном описанному в вопросе. Похоже, что при подобных обстоятельствах это может дать вам решение, которое вы ищете. Кроме того, кажется, что этот быстрый и грязный метод все еще работает!

Answer 3

@ Виктор Энгель: Спасибо за разъяснения. Теперь решение стало еще проще.

Короче, посмотрите на крутящие моменты обеих кривых. Если они сближаются, возникает "перегиб", если они противоположны, "кривизна" продолжается.

Примечание: слова "изгиб" и "кривизна" имеют здесь более интуитивную природу, чем строгое математическое значение, поэтому используются апострофы.

Как и прежде, набор точек P0,P1,P2,P3 определяет первую кубическую кривую Безье, а Q0,Q1,Q2 и Q3 - вторую. Более того, 4 вектора: a, b, u, w будут полезны.

a = P2P3
b = P1P2
u = Q0Q1
v = Q1Q2

Я не буду проверять непрерывность C1, это уже сделано вами. (Это означает, что P3=Q0 и a x u= 0)

Наконец, крутящие моменты Tp и Tq появятся.

Tp = b x a 

("x" означает векторное произведение, но Tp на плоскости обрабатывается как простое число, а не как вектор. }

if Tp=0            {very rarely vectors a, b can be parallel.}
    b = P0P1
    Tp = b x a 
    if Tp=0 
        No! It's can't be! Who straightened the curve???
        STOP
    endif
endif

Tq = u x v 
if Tq=0            {also  vectors u, v can be parallel.}
    v = Q2Q3
    Tq = u x v 
    if Tq=0 
        Oh no! What happened to my curve???
        STOP
    endif
endif

Теперь финальный тест:

if Tp*Tq < 0  then    Houston! We have AN "INFLEXION"!
              else    WE CONTINUE THE TURN!

Answer 4

Предположим, у вас есть 4 точки: P0, P1, P2 и P3, которые описывают кубическую кривую Безье (сокращенно cBc) . P0 и P3 - начальная и конечная точки, P1 и P2 - направленные точки.

Когда P0, P1 и P2 коллинеарны, то cBc имеет точку перегиба в P0.

Когда P1, P2 и P3 коллинеарны, тогда cBC имеет точку перегиба в P3.

Замечания.

1) Используйте векторное произведение ( P0P1 x P1P2 и P1P2 x P2P3 соответственно), чтобы проверить коллинеарность. Результатом должен быть вектор нулевой длины.

2) Избегайте ситуации, когда P0, P1, P2 и P3 все коллинеарны, а создаваемые ими cBc не являются кривыми в обычном смысле.

Следствие.

Когда P1 = P2, cBc имеет точки перегиба с обеих сторон.