Кривая Безье с контрольными точками внутри кривой

Question

Пожалуйста, смотрите изображение ниже. 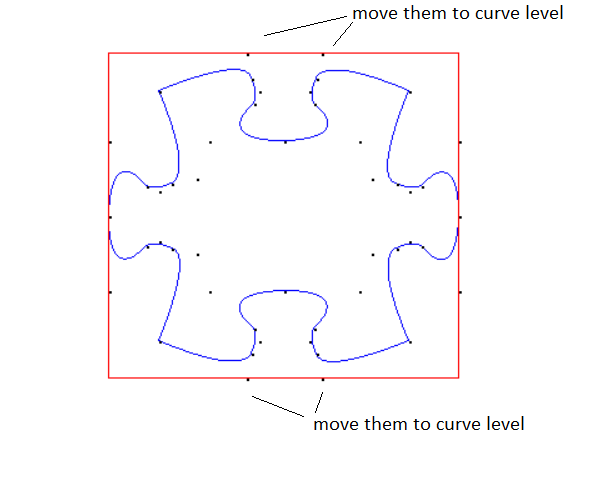Этот объект пути создается с использованием кривой Безье по 4 с каждой стороны. В настоящее время я сталкиваюсь с проблемой, когда пытаюсь получить границы этого объекта пути, созданного с использованием кривых кубической жаровни. Как вы можете видеть, верхняя и нижняя стороны имеют контрольную точку вдали от кривой, что делает границы абсолютно неточными.

Поэтому мой вопрос заключается в том, можно ли создать кусок головоломки, как на изображении, со всеми контрольными точками на или на уровне кривой. (Это создание кривой и идеальное ее отражение, все точки в пределах кривой)

Answer 1

Не рассчитывайте границы, используя контрольные точки. По крайней мере, если вам нужны жесткие границы и вы не хотите быстро проверять потенциальную видимость в данном прямоугольнике отсечения. Этот удивительный сайт может очень помочь с общими вычислениями кривой Безье, включая ограничивающую рамку.

В качестве альтернативы, переключитесь на сплайны, где контрольные точки находятся на кривой, но тогда вы можете получить обратный эффект, когда кривая выходит за границы, наложенные контрольными точками.

Answer 2

Одним из свойств кривых Безье является то, что при их разбиении расстояние между гладкой кривой и CV сокращается.

Таким образом, один из способов исправить эти резюме сверху и снизу - разделить связанный Безье на два Безье, используя алгоритм Де Кастельжау.

Вы могли бы даже сделать это алгоритмически:

• Найдите плотную ограничивающую рамку и ограничивающую рамку на основе CV.
• Если разница больше вашей терпимости, найдите максимальные / минимальные резюме и связанные с ними кривые Безье.
• Разделите все связанные кривые Безье на две кривые Безье каждая
• Повторение

В конце концов вы достигнете своей терпимости. К тому времени у вас может быть много Безье, если у вас очень жесткие допуски или хитрые данные.

Answer 3

Вы можете легко преобразовать свои кубические контрольные точки BEZIER в кубическую интерполяцию. Просто изменив это:

• БЕЗЬЕР против кубической интерполяции

так:

/*                              bezier = interpol
1  |                           (    x0)=X1;
t  |                  (3.0*x1)-(3.0*x0)=(0.5*(X2-X0));
tt |         (3.0*x2)-(6.0*x1)+(3.0*x0)=(3.0*(X2-X1))-(X2-X0)-(0.5*(X3-X1));
ttt|(    x3)-(3.0*x2)+(3.0*x1)-(    x0)=(0.5*(X2-X0))+(0.5*(X3-X1))+(2.0*(-X2+X1));
1  |                           (    y0)=Y1;
t  |                  (3.0*y1)-(3.0*y0)=(0.5*(Y2-Y0));
tt |         (3.0*y2)-(6.0*y1)+(3.0*y0)=(3.0*(Y2-Y1))-(Y2-Y0)-(0.5*(Y3-Y1));
ttt|(    y3)-(3.0*y2)+(3.0*y1)-(    y0)=(0.5*(Y2-Y0))+(0.5*(Y3-Y1))+(2.0*(-Y2+Y1));
*/

// input: x0,y0,..x3,y3 ... Bezier control points
// output: X0,Y0,..X3,Y3  ... interpolation control points
    double x0,y0,x1,y1,x2,y2,x3,y3,m=1.0/9.0;
    X0=x0-(x1-x0)/m; Y0=y0-(y1-y0)/m;
    X1=x0;           Y1=y0;
    X2=x3;           Y2=y3;
    X3=x3+(x3-x2)/m; Y3=y3+(y3-y2)/m;

Надеюсь, я не совершил ни одной алгебраической ошибки. Это переместит все контрольные точки в ваши кривые напрямую, пока форма не изменится. Помните, что для расчета BBOX следует использовать только (X1,Y1) а также (X2,Y2) в качестве используемого параметра t=<0,1> интерполирует между ними!!!

Но даже это может привести к неточности, так как вы можете иметь некоторые крайности без контрольной точки. В случае, если даже это является проблемой (BBOX немного меньше, чем следует), вы можете повторно сэмплировать свою форму в набор точек (например, 10 на кубический) на кривой с некоторым шагом (0.1) и сделать BBOX из этих точек. Это будет гораздо точнее, но грубее медленнее...