Как я могу подогнать кривую Безье к набору данных?
У меня есть набор точек данных (которые я могу прореживать), которые мне нужны, чтобы соответствовать кривой Безье. Мне нужна скорость, а не точность, но подгонка должна быть достаточно приличной, чтобы ее можно было узнать. Я также ищу алгоритм, который я могу использовать, который не использует библиотеки (особенно NumPy).
Я прочитал несколько исследовательских работ, но ни одна из них не содержит достаточно подробностей для полной реализации. Есть ли примеры с открытым исходным кодом?
7 ответов
У меня похожая проблема, и я нашел "Алгоритм автоматического подбора оцифрованных кривых" от Graphics Gems (1990) о подгонке кривой Безье. В дополнение к этому я нашел исходный код для этой статьи.
К сожалению, это написано на C, который я не очень хорошо знаю. Также алгоритм довольно сложен для понимания (по крайней мере, для меня). Я пытаюсь перевести его на C# код. Если я буду успешным, я постараюсь поделиться этим.
файл GGVecLib.c в той же папке, что и FitCurves.c содержит основные векторы манипуляции функциями.
Я нашел похожий вопрос переполнения стека, сглаживая нарисованную вручную кривую. Утвержденный ответ предоставляет код C# для алгоритма подбора кривой от Graphic Gems.
Чего не хватает во многих из этих ответов, так это того, что вы, возможно, не захотите вписывать в свои данные одну кубическую кривую Безье. В более общем случае вы хотели бы подогнать последовательность произвольных кубических кривых Безье, т.е. кусочно-кубическое соответствие Безье, произвольному набору данных.
Есть хороший тезис, датированный 1995 годом, в комплекте с кодом MATLAB, который делает это:
% Lane, Edward J. Fitting Data Using Piecewise G1 Cubic Bezier Curves.
% Thesis, NAVAL POSTGRADUATE SCHOOL MONTEREY CA, 1995
http://www.dtic.mil/dtic/tr/fulltext/u2/a298091.pdf
Чтобы использовать это, вы должны, как минимум, указать количество точек узла, т. Е. Количество точек данных, которые будут использоваться подпрограммами оптимизации для подбора. При желании вы можете указать сами узлы, что повышает надежность посадки. Тезис показывает несколько довольно жестких примеров. Обратите внимание, что подход Лейна гарантирует непрерывность G1 (направления смежных касательных векторов идентичны) между кубическими сегментами Безье, т.е. гладкими соединениями. Однако могут быть разрывы в кривизне (изменения в направлении второй производной).
Я переопределил код, обновив его до современного MATLAB (R2015b). Свяжитесь со мной, если хотите.
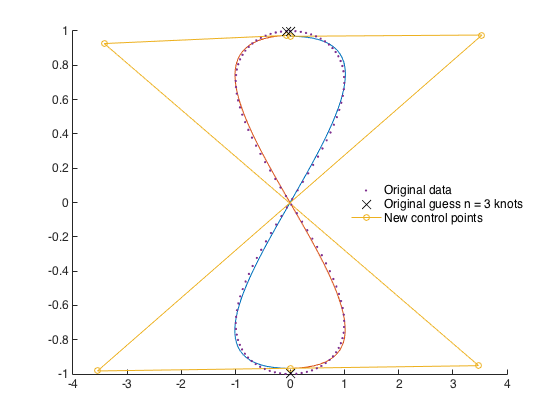
Вот пример использования только трех узловых точек (выбираемых автоматически кодом) для подгонки двух кубических сегментов Безье к фигуре Лиссажу.
Вы можете настроить задачу как наименьших квадратов, подходящих для шумных данных.
Смотрите http://nbviewer.ipython.org/5688579
Обратите внимание, что как только вы выясните уравнения, фактическое вычисление будет довольно простым. Фактические вычисления суммируют данные, а затем инвертируют и умножают матрицу 4х4.
Я знаю, что эта тема давно устарела, но я обнаружил, что это интересная проблема на случай, если кто-то еще наткнется на нее.
См. http://www.embedded.com/electrical-engineer-community/industry-blog/4027019/1/Why-all-the-math- для отличного учебника по наименьшим квадратам.
Если большая часть данных соответствует модели, вы можете попробовать RANSAC. Было бы достаточно легко выбрать 4 и случайные точки и подобрать кривую Безье из них. Я не совсем уверен, насколько дорого будет оценивать кривую по всем остальным точкам (часть алгоритма RANSAC). Но это было бы линейным решением, и RANSAC действительно легко написать (и, вероятно, существуют алгоритмы с открытым исходным кодом).
Здесь вы найдете реализацию Python упомянутого кода на языке Python. https://github.com/volkerp/fitCurves
У меня было решение MATLAB для этой проблемы. Я столкнулся с той же проблемой, но мой код написан на MATLAB. Надеюсь, это не так сложно перевести на Python.
Вы можете найти контрольные точки по этому коду FindBezierControlPointsND.m По какой-то причине у него нет функции "ChordLengthNormND" в его архиве, но она вызывается в строке 45.
Я заменил его следующими строками:
[arclen,seglen] = arclength(p(:,1),p(:,2),'sp');
t = zeros(size(p,1),1);
sums = seglen(1);
for i = 2:size(p,1)-1
t(i) = sums / arclen;
sums = sums + seglen(i);
end
t(end) = 1;
MATLAB-код arclength можно получить здесь.
После этого у нас есть контрольные точки для кривой Безье, и есть множество реализаций построения кривой Безье по контрольным точкам в сети.
Прежде всего, убедитесь, что то, что вы просите, на самом деле то, что вы хотите. Подгонка точек к кривой Безье поместит их в корпус точек. Использование сплайна позволит вашей кривой пройти все точки.
Тем не менее, создание функции, которая рисует либо совсем не сложно. В Википедии есть хорошая статья, которая объяснит основы, кривую Безье.