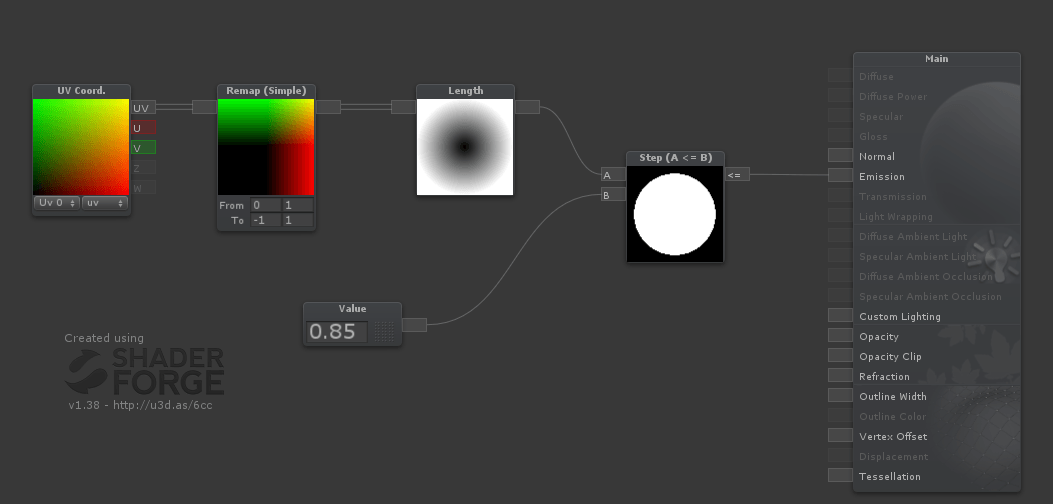
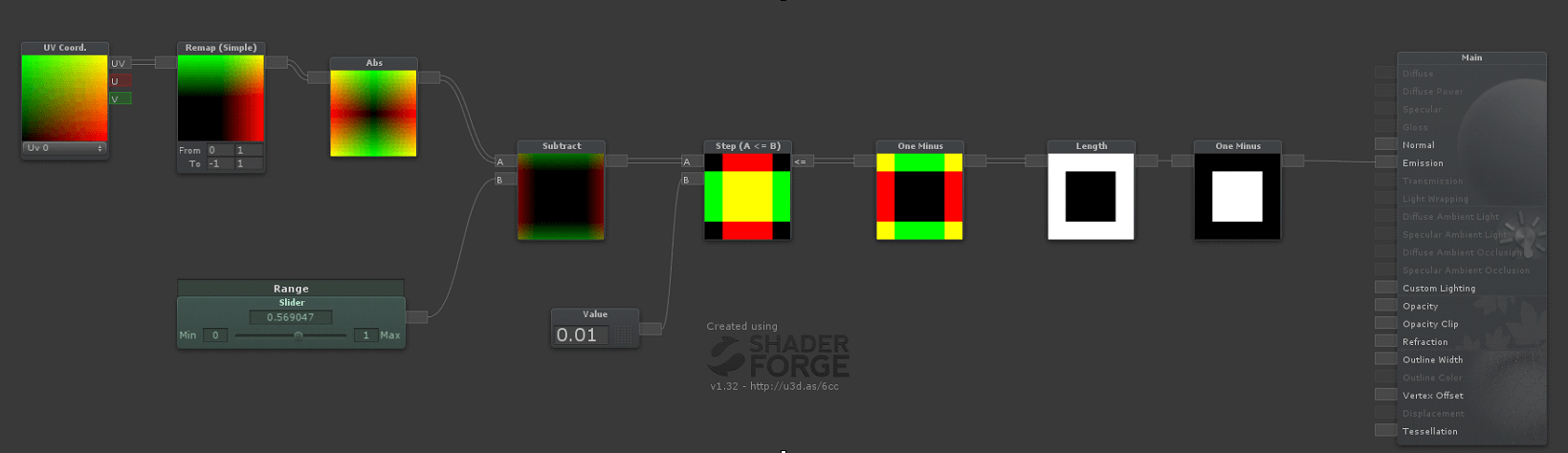
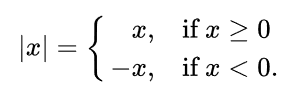GLSL куб подписал объяснение реализации поля расстояния?

Я смотрю и пытаюсь понять следующий фрагмент кода

float sdBox( vec3 p, vec3 b )
{
  vec3 d = abs(p) - b;
  return min(max(d.x,max(d.y,d.z)),0.0) +
         length(max(d,0.0));
}

Я это понимаю length(d) обрабатывает случай SDF, где точка смещена к "углу" (т. е. все компоненты d положительны) и что max(d.x, d.y, d.z) дает нам правильное расстояние во всех других случаях. Что я не понимаю, так это то, как эти две комбинации объединяются здесь без использования оператора if для проверки признаков dКомпоненты.

Когда все d компоненты положительны, выражение возврата может быть уменьшено до length(d) из-за пути min/max будет оценивать - и когда все d компоненты отрицательные, мы получаем max(d.x, d.y, d.z), Но как я должен понимать промежуточные дела? Те, где компоненты d есть смешанные знаки?

Я пытался объяснить это безрезультатно. Я был бы очень признателен, если бы кто-то мог объяснить это мне в геометрических / математических терминах. Благодарю.

Источник

2 ответа

Если вы хотите узнать, как это работает, лучше сделайте следующие шаги:

1. Прежде всего вы должны знать определения форм

2. Всегда лучше рассмотреть их 2D-форму, потому что три измерения могут быть сложными для вас.

Итак, позвольте мне объяснить некоторые формы:

Круг

Круг

Круг - это простая замкнутая форма. Это набор всех точек на плоскости, которые находятся на заданном расстоянии от заданной точки, центра.

Ты можешь использовать distance(), length() или же sqrt() рассчитать расстояние до центра рекламного щита.

Книга шейдеров - Глава 7

Площадь

Площадь

В геометрии квадрат представляет собой правильный четырехугольник, что означает, что он имеет четыре равные стороны и четыре равных угла (углы в 90 градусов).

Я описываю 2D-фигуры В разделе "Перед" теперь позвольте мне описать 3D-определение.

сфера

сфера

Сфера - это идеально круглый геометрический объект в трехмерном пространстве, представляющий собой поверхность полностью круглого шара.

Подобно кругу, который геометрически является объектом в двумерном пространстве, сфера определяется математически как набор точек, которые находятся на одинаковом расстоянии r от заданной точки, но в трехмерном пространстве. Refrence - Википедия

куб

куб

В геометрии куб - это трехмерный твердый объект, ограниченный шестью квадратными гранями, гранями или сторонами, по три встречи в каждой вершине. Ссылка: Википедия

Моделирование с функциями расстояния

Теперь пришло время для понимания моделирования с помощью функций расстояния

сфера

Как упоминалось в последних разделах. В приведенном ниже коде length() используется для расчета расстояния до центра рекламного щита, и вы можете масштабировать эту форму по параметру s.

//Sphere - signed - exact
/// <param name="p">Position.</param>
/// <param name="s">Scale.</param>
float sdSphere( vec3 p, float s )
{
  return length(p)-s;
}

коробка

// Box - unsigned - exact
/// <param name="p">Position.</param>
/// <param name="b">Bound(Scale).</param> 
float udBox( vec3 p, vec3 b )
{
  return length(max(abs(p)-b,0.0));
}

length() используется как предыдущий пример. дальше у нас есть max(x,0) Это называется положительными и отрицательными частями 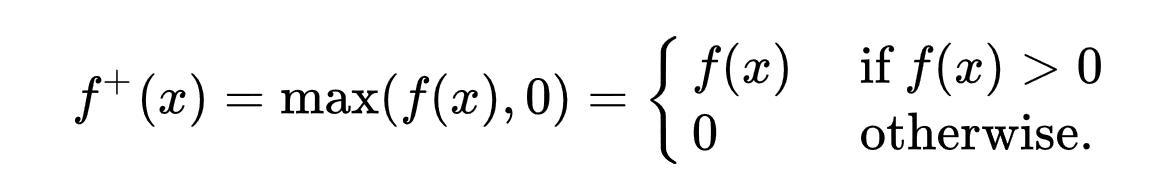Positive_and_negative_parts

это означает, что приведенный ниже код эквивалентен:

float udBox( vec3 p, vec3 b )
{

   vec3 value = abs(p)-b;


   if(value.x<0.){
   value.x = 0.;  
   }

  if(value.y<0.){
  value.y = 0.;  
  }

  if(value.z<0.){
  value.z = 0.;  
  }  

  return length(value);
}

шаг 1

   if(value.x<0.){
   value.x = 0.;  
   }

шаг 1

шаг 2

  if(value.y<0.){
  value.y = 0.;  
  }

шаг 2

шаг 3

  if(value.z<0.){
  value.z = 0.;  
  }

шаг 3

шаг 4

Далее у нас есть функция отпущения грехов. Она используется для удаления дополнительных деталей.

отпущение грехов

step4

Шаги отпущения грехов

шаг 3

Шаг отпущения грехов 1

if(value.x < -1.){
   value.x = 1.; 
}

Abs1

Шаг отпущения грехов 2

if(value.y < -1.){
value.y = 1.; 
}

ABS2

Шаг отпущения грехов 3

if(value.z < -1.){
value.z = 1.; 
}

step4

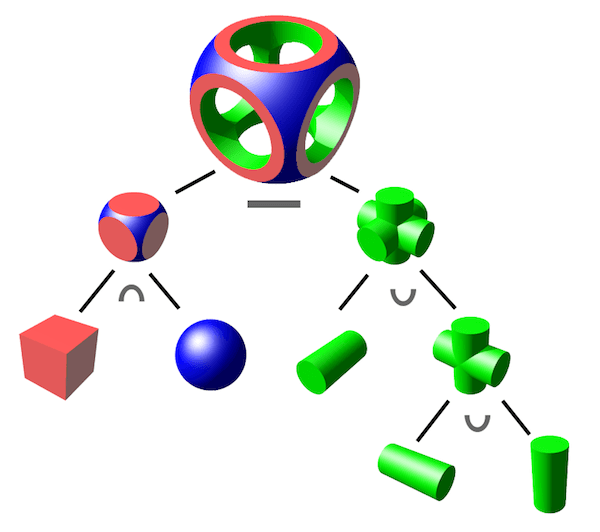
Также вы можете сделать любую форму, используя Конструктивную геометрию твердого тела.

Конструктивная геометрия твердого тела

CSG построен на 3 примитивных операциях: пересечение (∩), союз (∪) и разница (-).

Оказывается, что все эти операции кратко выражены при объединении двух поверхностей, выраженных как SDF.

intersectSDF

float intersectSDF(float distA, float distB) {
    return max(distA, distB);
}

unionSDF

float unionSDF(float distA, float distB) {
    return min(distA, distB);
}

differenceSDF

float differenceSDF(float distA, float distB) {
    return max(distA, -distB);
}
Источник

Я понял это некоторое время назад и много писал об этом в блоге здесь: http://fabricecastel.github.io/blog/2016-02-11/main.html

Вот выдержка (см. Полный пост для полного объяснения):

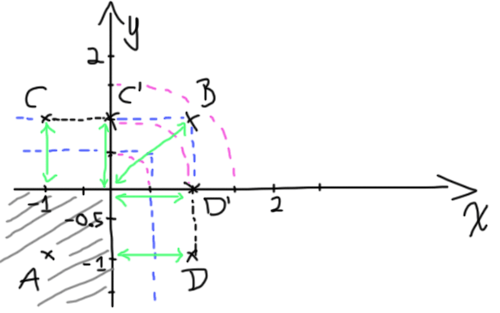
Рассмотрим четыре точки, A, B, C и D. Давайте грубо уменьшим функцию расстояния, чтобы попытаться избавиться от функций min / max, чтобы понять их влияние (поскольку именно это и вызывает недоумение в этой функции). Обозначения ниже немного небрежно, я использую квадратные скобки для обозначения 2D векторов.

// 2D version of the function
d(p) = min(max(p.x, p.y), 0)
       + length(max(p, 0))

---

d(A) = min(max(-1, -1), 0)
       + length(max([-1, -1], 0))

d(A) = -1 + length[0, 0]

---

d(B) = min(max(1, 1), 0)
       + length(max([1, 1], 0))

d(B) = 0 + length[1, 1]

Хорошо, пока ничего особенного. Когда A находится внутри квадрата, мы по существу получаем нашу первую функцию расстояния, основанную на плоскостях / линиях, а когда B находится в области, где наша первая функция расстояния неточна, она обнуляется, и мы получаем вторую функцию расстояния (длину). Хитрость заключается в двух других случаях C и D. Давайте разберемся с ними.

d(C) = min(max(-1, 1), 0)
      + length(max([-1, 1], 0))

d(C) = 0 + length[0, 1]

---

d(D) = min(max(1, -1), 0)
       + length(max([-1, 1], 0))

d(D) = 0 + length[1, 0]

Если вы посмотрите на график выше, вы заметите C'и D'. Эти точки имеют координаты [0,1] и [1,0] соответственно. Этот метод использует тот факт, что оба поля расстояния пересекаются по осям - D и D 'находятся на одинаковом расстоянии от квадрата.

Если мы обнуляем все отрицательные компоненты вектора и берем его длину, мы получим правильное расстояние между точкой и квадратом (только для точек вне квадрата). Это то, что делает max(d,0.0); компонентная максимальная операция. До тех пор, пока у вектора есть хотя бы один положительный компонент, min(max(dx,dy),0.0) будет разрешаться до 0, оставляя нам только вторую часть уравнения. В том случае, если точка находится внутри квадрата, мы хотим вернуть первую часть уравнения (поскольку она представляет нашу первую функцию расстояния). Если все компоненты вектора отрицательны, легко увидеть, что наше условие будет выполнено.

Это понимание должно переместиться обратно в 3D, как только вы обернетесь вокруг него. Возможно, вам придется или не придется рисовать несколько графиков от руки, чтобы действительно "получить" их - я знаю, что сделал, и рекомендовал бы вам сделать это, если вы недовольны моим объяснением.

Работая с этой реализацией в нашем собственном коде, мы получаем это:

float distanceToNearestSurface(vec3 p){
  float s = 1.0;
  vec3 d = abs(p) - vec3(s);
  return min(max(d.x, max(d.y,d.z)), 0.0)
      + length(max(d,0.0));
}

И там у вас есть это.

Источник
Другие вопросы по тегам