Генерация плоскости с треугольными полосами

Question

Какой будет лучший алгоритм для генерации списка вершин для рисования плоскости с использованием треугольных полос?

Я ищу функцию, которая получает ширину и высоту плоскости и возвращает массив с плавающей точкой, содержащий правильно проиндексированные вершины.

ширина представляет количество вершин в строке.

высота представляет количество вершин в столбце.

float* getVertices( int width, int height ) {
    ...
}

void render() {
    glEnableClientState(GL_VERTEX_ARRAY);
    glVertexPointer(3, GL_FLOAT, 0, getVertices(width,heigth));
    glDrawArrays(GL_TRIANGLE_STRIP, 0, width*height);
    glDisableClientState(GL_VERTEX_ARRAY);
}

Answer 1

Спасибо вам всем. Я закодировал это. Это правильно? Или сгенерированная полоса как-то не так?

int width;
int height;
float* vertices = 0;
int* indices = 0;

int getVerticesCount( int width, int height ) {
    return width * height * 3;
}

int getIndicesCount( int width, int height ) {
    return (width*height) + (width-1)*(height-2);
}

float* getVertices( int width, int height ) {
    if ( vertices ) return vertices;

    vertices = new float[ getVerticesCount( width, height ) ];
    int i = 0;

    for ( int row=0; row<height; row++ ) {
        for ( int col=0; col<width; col++ ) {
            vertices[i++] = (float) col;
            vertices[i++] = 0.0f;
            vertices[i++] = (float) row;
        }
    }

    return vertices;
}

int* getIndices( int width, int height ) {
    if ( indices ) return indices;

    indices = new int[ iSize ];
    int i = 0;

    for ( int row=0; row<height-1; row++ ) {
        if ( (row&1)==0 ) { // even rows
            for ( int col=0; col<width; col++ ) {
                indices[i++] = col + row * width;
                indices[i++] = col + (row+1) * width;
            }
        } else { // odd rows
            for ( int col=width-1; col>0; col-- ) {
                indices[i++] = col + (row+1) * width;
                indices[i++] = col - 1 + + row * width;
            }
        }
    }
    if ( (mHeight&1) && mHeight>2 ) {
        mpIndices[i++] = (mHeight-1) * mWidth;
    }

    return indices;
}

void render() {
    glEnableClientState( GL_VERTEX_ARRAY );
    glVertexPointer( 3, GL_FLOAT, 0, getVertices(width,height) );
    glDrawElements( GL_TRIANGLE_STRIP, getIndicesCount(width,height), GL_UNSIGNED_INT, getIndices(width,height) );
    glDisableClientState( GL_VERTEX_ARRAY );
}

С шириной =4 и высотой =4 вот что я получил: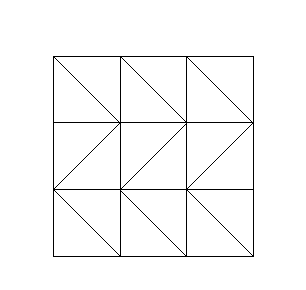

И здесь я изменяю высоту некоторых вершин:

Answer 2

Вот код, который делает это (не проверено, но, по крайней мере, вы поняли идею):

void make_plane(int rows, int columns, float *vertices, int *indices) {
    // Set up vertices
    for (int r = 0; r < rows; ++r) {
        for (int c = 0; c < columns; ++c) {
            int index = r*columns + c;
            vertices[3*index + 0] = (float) c;
            vertices[3*index + 1] = (float) r;
            vertices[3*index + 2] = 0.0f;
        }
    }

    // Set up indices
    int i = 0;
    for (int r = 0; r < rows - 1; ++r) {
        indices[i++] = r * columns;
        for (int c = 0; c < columns; ++c) {
            indices[i++] = r * columns + c;
            indices[i++] = (r + 1) * columns + c;
        }
        indices[i++] = (r + 1) * columns + (columns - 1);
    }
 }

Первый цикл устанавливает массив вершин в стандартной прямоугольной сетке. Есть R*C вершины.

Второй цикл устанавливает индексы. Как правило, в сетке две вершины на квадрат. Каждая вершина приведет к рисованию нового треугольника (с двумя предыдущими вершинами), поэтому каждый квадрат рисуется с двумя треугольниками.

Первая и последняя вершины в начале и конце каждой строки дублируются. Это означает, что между каждым рядом есть два треугольника нулевой области (вырожденные треугольники). Это позволяет нам нарисовать всю сетку в одну большую полосу треугольника. Эта техника называется шить.

Answer 3

Ни один из приведенных выше кодов не дает правильной генерации сетки. Очень хорошая статья о том, как сделать полосу треугольников на простой плоскости: http://www.learnopengles.com/android-lesson-eight-an-introduction-to-index-buffer-objects-ibos/

Вот мой тестовый код, который фактически протестирован и полностью работает:

int plane_width = 4; // amount of columns
int plane_height = 2; // amount of rows

int total_vertices = (plane_width + 1) * (plane_height + 1);
planeVert = new CIwFVec2[total_vertices];
memset(planeVert, 0, sizeof(CIwFVec2) * total_vertices);

int numIndPerRow = plane_width * 2 + 2;
int numIndDegensReq = (plane_height - 1) * 2;
int total_indices = numIndPerRow * plane_height + numIndDegensReq;

planeInd = new uint16[total_indices];

make_plane(plane_width, plane_height, planeVert, planeInd);

...

void make_plane(int width, int height, CIwFVec2 *vertices, uint16 *indices)
{
width++;
height++;

int size = sizeof(CIwFVec2);
// Set up vertices
for(int y = 0; y < height; y++)
{
    int base = y * width;
    for(int x = 0; x < width; x++)
    {
        int index = base + x;
        CIwFVec2 *v = vertices + index;
        v->x = (float) x;
        v->y = (float) y;
        Debug::PrintDebug("%d: %f, %f", index, v->x, v->y);
    }
}

Debug::PrintDebug("-------------------------");

// Set up indices
int i = 0;
height--;
for(int y = 0; y < height; y++)
{
    int base = y * width;

    //indices[i++] = (uint16)base;
    for(int x = 0; x < width; x++)
    {
        indices[i++] = (uint16)(base + x);
        indices[i++] = (uint16)(base + width + x);
    }
    // add a degenerate triangle (except in a last row)
    if(y < height - 1)
    {
        indices[i++] = (uint16)((y + 1) * width + (width - 1));
        indices[i++] = (uint16)((y + 1) * width);
    }
}

for(int ind=0; ind < i; ind++)
    Debug::PrintDebug("%d ", indices[ind]);
}

Answer 4

Я делал что-то подобное и, используя первые два ответа, я придумал это (проверено, C#, XNA)

        // center x,z on origin
        float offset = worldSize / 2.0f, scale = worldSize / (float)vSize;

        // create local vertices
        VertexPositionColor[] vertices = new VertexPositionColor[vSize * vSize];

        for (uint z = 0; z < vSize; z++) {
            for (uint x = 0; x < vSize; x++) {
                uint index = x + (z * vSize);
                vertices[index].Position = new Vector3((scale*(float)x) - offset, 
                                                       heightValue, 
                                                       (scale*(float)z) - offset);
                vertices[index].Color = Color.White;
            }
        }

        // create local indices
        var indices = new System.Collections.Generic.List<IndexType>();

        for (int z = 0; z < vSize - 1; z++) {
            // degenerate index on non-first row
            if (z != 0) indices.Add((IndexType)(z * vSize));

            // main strip
            for (int x = 0; x < vSize; x++) {
                indices.Add((IndexType)(z * vSize + x));
                indices.Add((IndexType)((z + 1) * vSize + x));
            }

            // degenerate index on non-last row
            if (z != (vSize-2)) indices.Add((IndexType)((z + 1) * vSize + (vSize - 1)));
        }

Это легко конвертируется в C++, просто сделайте indices std::vector.

Для моего решения характерны следующие особенности: а) Нет необходимости изменять порядок намотки для каждой подполосы - добавление двух точек создает два вырожденных треугольника, поэтому порядок для следующей подполосы правильный. б) Вы должны условно добавить первую и последнюю вершины треугольника dg.