JAGS: распространение априора внутри дистрибутива

Question

Это наша первая модель:

# Data:
x1 = as.factor(c(0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1))
x2 = as.factor(c(0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1))
x3 = as.factor(c(0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1))
x4 = as.factor(c(0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1))
n = rep(1055, 16)
y = c(239, 31, 15, 11, 7, 5, 18, 100, 262, 32, 38, 32, 8, 7, 16, 234)

# Model:
mymodel = function(){
  for (i in 1:16){
    y[i] ~ dbin(theta[i], n[i] )
    eta[i] <- gamma*x1[i]+beta1*x2[i]+beta2*x3[i]+beta3*x4[i]
    theta[i] <- 1/(1+exp(-eta[i]))
  }

  # Prior
  gamma ~ dnorm(0,0.00001) 
  beta1 ~ dnorm(0,0.00001)
  beta2 ~ dnorm(0,0.00001)
  beta3 ~ dnorm(0,0.00001)
}

Теперь нас просят добавить альфа как нормальное с известным средним и неизвестной дисперсией. Но дисперсия имеет одинаковый априор, как показано на рисунке:

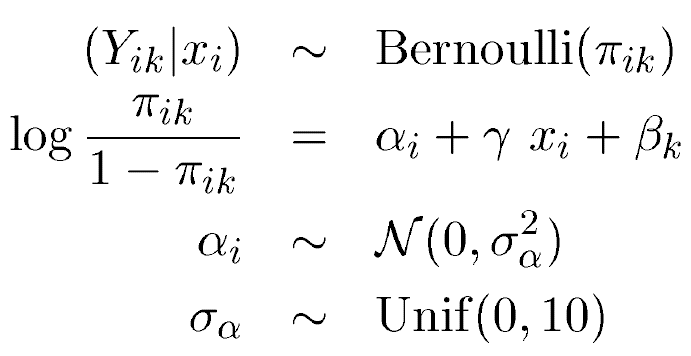
Я не знаю, как добавить альфа в модель, а затем указать новый параметр в приоры...

Answer 1

Вы бы просто добавили alpha в ваш линейный предиктор и дать ему распределение, как и любой другой параметр. Тем не мение, JAGS параметризовывает нормальное распределение как точность вместо дисперсии (точность является обратной величиной дисперсии). Модель будет выглядеть примерно так. Также вы можете просто использовать logit(eta) вместо применения обратного логита.

mymodel = function(){
  for (i in 1:16){
    y[i] ~ dbin(eta[i], n[i] )
    logit(eta[i]) <- alpha + gamma*x1[i]+beta1*x2[i]+beta2*x3[i]+beta3*x4[i]
  }

  # Prior
  alpha ~ dnorm(0, tau_alpha)
  tau_alpha <- 1 / var_alpha
  var_alpha ~ dunif(0, 10)
  gamma ~ dnorm(0,0.00001) 
  beta1 ~ dnorm(0,0.00001)
  beta2 ~ dnorm(0,0.00001)
  beta3 ~ dnorm(0,0.00001)
}