Алгоритм "Магический квадрат"
В качестве эксперимента я пытаюсь создать программу для магического квадрата, которая проверяет каждый возможный квадрат с девятью числами. Для тех, кто не знает, магический квадрат - это сетка 3х3 с числами 1-9, где каждая строка, столбец и диагональ составляют в сумме 15. Например:
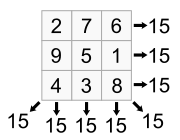
Как мне проверить каждый квадрат, используя таблицу с Lua? Я начинаю со следующей таблицы:
local sq = {
1, 1, 1,
1, 1, 1
1, 1, 1
}
Как мне проверить каждую таблицу в правильном порядке? Я могу нарисовать свои мысли на бумаге, но я не совсем уверен, как перевести это в код. Я уже создал функцию, чтобы проверить, является ли квадрат "магическим" (далее), но я не уверен, как правильно увеличить каждое число.
local isMagic = function(s)
return (
s[1] + s[2] + s[3] == 15 and
s[4] + s[5] + s[6] == 15 and
s[7] + s[8] + s[9] == 15 and
s[1] + s[4] + s[7] == 15 and
s[2] + s[5] + s[8] == 15 and
s[3] + s[6] + s[9] == 15 and
s[1] + s[5] + s[9] == 15 and
s[3] + s[5] + s[7] == 15
)
end
2 ответа
Исходя из того, что я вижу здесь, есть три модели:
1) if we can define step by 3, we compare columns:
sum(tab[x] for x in range(step)) == sum(tab[x] for x in xrange(step+1,step*2))== sum(tab[x] for x in xrange(2*step+1,step*3))
2) raws:
sum(tab[x] for x in range(step*step) if x%step==0) == sum(tab[x] for x in range(step*step) if x%step==1)== sum(tab[x] for x in range(step*step) if x%step==2) ===> till we x%step== step-1
3) Diagonales:
sum(tab[x] for x in range(step*step) if x%(step+1)==0) == sum(tab[x] for x in range(step*step) if x%(step+1)==step-1)
Прежде всего, у вас есть набор 2D, почему вы используете 1D список? Я бы предпочел, чтобы ваш квадрат был похож
square[1-3][1-3]
Таким образом, вы можете просто проверить каждую строку в X и каждую строку в Y, а затем проверить 2 диагонали.
скорее, чем
square[1-9]
Вы должны жестко закодировать проверки в этом решении, которые не позволят вам установить другие размеры квадратов без нового кодирования.
Как:
local square = {}
square[1] = {[1] = 2, [2] = 7, [3] = 6}
square[2] = {[1] = 9, [2] = 5, [3] = 1}
square[3] = {[1] = 4, [2] = 3, [3] = 8}
Вот мой код для проверки, является ли квадрат магическим или нет. Вы можете установить размер, как вы хотите.
#!/usr/local/bin/lua
function checkTheSquare(square, check_for)
local dia_sum = 0 -- we will add the diagonal(u.l. to l.r.) values here
local inv_dia_sum = 0 -- we will add the diagonal(u.r. to l.l.) values here
for i = 1, #square do -- for every [i] line in square
local temp_sum = 0 -- just holds the values for the [i] line temporary
for j = 1, #square do -- for every [j] line in square
temp_sum = temp_sum + square[i][j] -- add the square[i][j] value to temp
end
dia_sum = dia_sum + square[i][i]
-- this will go like: [1][1] -> [2][2] -> [3][3] ...
inv_dia_sum = inv_dia_sum + square[i][#square-i+1]
-- this will go like: [1][3] -> [2][2] -> [3][1] ...
if temp_sum ~= check_for then return false end
-- first possible find of wrong line -> NOT MAGIC
end
if dia_sum ~= check_for and inv_dia_sum ~= check_for then
return false
-- due its not magic
end
return true
-- ITS MAGIC! JUHUUU
end
local square = {}
square[1] = {[1] = 16, [2] = 3, [3] = 2, [4] = 13}
square[2] = {[1] = 5, [2] = 10, [3] = 11, [4] = 8}
square[3] = {[1] = 9, [2] = 6, [3] = 7, [4] = 12}
square[4] = {[1] = 4, [2] = 15, [3] = 14, [4] = 1}
local check_for = 34
print(checkTheSquare(square, check_for) == true)
по сравнению с вашим собственным кодом он выглядит более сложным, но:
- Ваш не алгоритм, это процедура.
- Мой динамичный. Можно также добавить случайные значения в квадратные поля, переставив, сколько попыток потребуется в среднем, чтобы получить магический квадрат.