Описание нелинейного преобразования между двумя изображениями с использованием гомографии
Между двумя точками на двух изображениях уже установлено однозначное соответствие.
Image2 - искаженная версия image1. Модель искажения, кажется, искажение хрусталика глаза. Вопрос заключается в следующем: есть ли способ вычислить матрицу преобразования, которая описывает этот переход. На самом деле матрица, которая преобразует синие точки на первом изображении в соответствующие им синие точки на втором изображении? Проблема здесь в том, что мы не знаем фокусного расстояния (это означает, что изображения не откалиброваны), однако у нас есть идеальное соответствие между 200 точками на двух изображениях.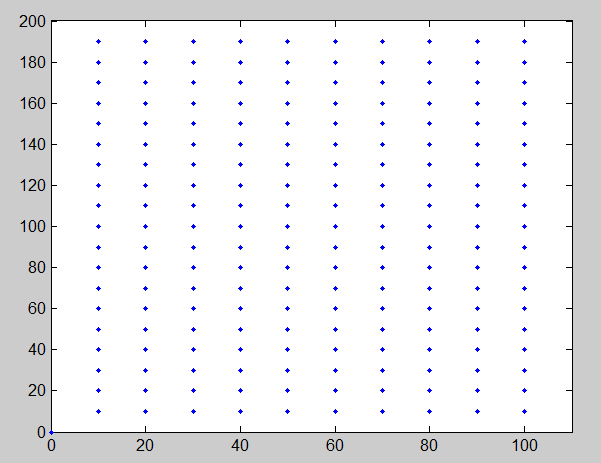 искаженное изображение:
искаженное изображение: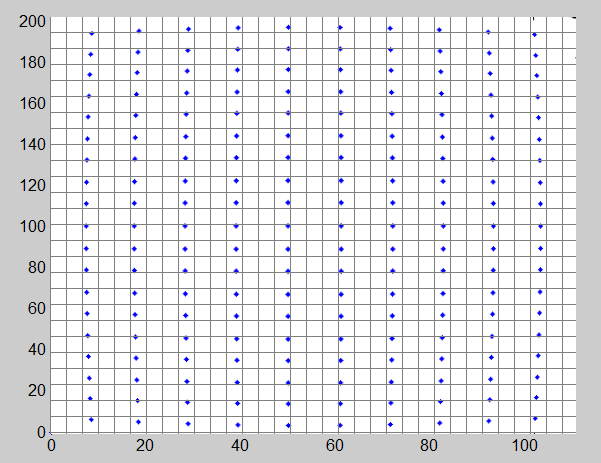
1 ответ
Я думаю, что то, что вы пытаетесь сделать, можно рассматривать как проблему коррекции искажений, без необходимости остальной части классической калибровки камеры.
Матричное преобразование является линейным, и линейные преобразования всегда отображают прямые линии в прямые ( http://en.wikipedia.org/wiki/Linear_map). Из рисунка видно, что преобразование является нелинейным, поэтому вы не можете описать его с помощью матричной операции.
Тем не менее, вы можете использовать модель искажения объектива, подобную той, которая используется OpenCV ( http://docs.opencv.org/doc/tutorials/calib3d/camera_calibration/camera_calibration.html), и получение коэффициентов не должно быть очень трудным. Вот что вы можете сделать в Matlab:
Назовите (x, y) координаты исходной точки (верхнее изображение) и (xp, yp) координаты искаженной точки (нижнее изображение), оба сдвинуты в центр изображения и разделены на коэффициент масштабирования (то же самое для x и y) поэтому они лежат более или менее в интервале [-1, 1]. Модель искажения:
x = ( xp*(1 + k1*r^2 + k2*r^4 + k3*r^6) + 2*p1*xp*yp + p2*(r^2 + 2*xp^2));
y = ( yp*(1 + k1*r^2 + k2*r^4 + k3*r^6) + 2*p2*xp*yp + p1*(r^2 + 2*yp^2));
куда
r = sqrt(x^2 + y^2);
У вас есть 5 параметров: k1, k2, k3, p1, p2 для радиального и тангенциального искажения и 200 пар точек, так что вы можете решить нелинейную систему.
Убедитесь, что в рабочей области существуют массивы x, y, xp и yp, и объявите их глобальными:
global x y xp yp
Напишите функцию для оценки среднеквадратичной ошибки с учетом набора произвольных коэффициентов искажения, скажем, она называется "dist":
function val = dist(var)
global x y xp yp
val = zeros(size(xp));
k1 = var(1);
k2 = var(2);
k3 = var(3);
p1 = var(4);
p2 = var(5);
r = sqrt(xp.*xp + yp.*yp);
temp1 = x - ( xp.*(1 + k1*r.^2 + k2*r.^4 + k3*r.^6) + 2*p1*xp.*yp + p2*(r.^2 + 2*xp.^2));
temp2 = y - ( yp.*(1 + k1*r.^2 + k2*r.^4 + k3*r.^6) + 2*p2*xp.*yp + p1*(r.^2 + 2*yp.^2));
val = sqrt(temp1.*temp1 + temp2.*temp2);
Решите систему с помощью "fsolve":
[coef, fval] = fsolve(@dist, zeros(5,1));
Значения в 'coef' - это искомые коэффициенты искажения. Чтобы исправить искажение новых точек (xp, yp), отсутствующих в исходном наборе, используйте уравнения:
r = sqrt(xp.*xp + yp.*yp);
x_corr = xp.*(1 + k1*r.^2 + k2*r.^4 + k3*r.^6) + 2*p1*xp.*yp + p2*(r.^2 + 2*xp.^2);
y_corr = yp.*(1 + k1*r.^2 + k2*r.^4 + k3*r.^6) + 2*p2*xp.*yp + p1*(r.^2 + 2*yp.^2);
Результаты будут смещены в центр изображения и масштабированы в соответствии с коэффициентом, который вы использовали выше.
Заметки:
- Координаты должны быть смещены к центру изображения, так как искажение симметрично по отношению к нему.
- Нет необходимости в нормализации к интервалу [-1, 1], но это обычно делается, чтобы полученные коэффициенты искажения были более или менее одного и того же порядка (работая с степенями 2, 4 и 6 пикселей координаты будут нуждаться в очень малых коэффициентах).
- Этот метод не требует, чтобы точки на изображении находились в единой сетке.