Моделирование распределения образца не приводит к нормальному
Я пытался смоделировать "выборочное распределение выборочных пропорций" с использованием Python. Я попробовал с переменной Бернулли, как в примере здесь
Суть в том, что из большого количества гамболов у нас есть желтые шары с истинной пропорцией 0,6. Если мы возьмем образцы (некоторого размера, скажем, 10), возьмем среднее значение этого и построим график, мы должны получить нормальное распределение.
Я пытался сделать в Python, но я всегда получаю равномерное распределение (или в середине). Я не могу понять, что мне не хватает.
Программа:
from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt
N = 10000 # 10000 balls
p = 0.6 # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 1000 # sample size
n_experiments = 100 # I dont know what this is called
# generate population
population = create_bernoulli_population(N,p)
theor_df = get_frequency_df(population)
theor_df
# choose sample, take mean and add to X_mean_list. Do this for n_experiments times
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
X_hat = choices(population, k=n_pickups) # this method is with replacement
shuffle(population)
X_mean = sum(X_hat)/len(X_hat)
X_mean_list.append(X_mean)
# plot X_mean_list as bar graph
stats_df = get_frequency_df(X_mean_list)
fig, ax = plt.subplots(1,1, figsize=(5,5))
X = stats_df['x'].tolist()
P = stats_df['p(x)'].tolist()
ax.bar(X, P, color="C0")
plt.show()
Зависимые функции:
bi_to_nor_demo
SDSP
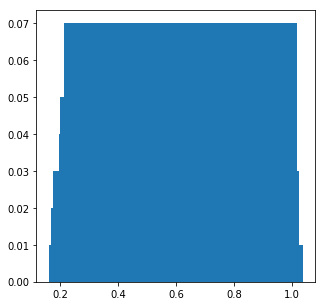
Обновление: я даже попробовал равномерное распределение, как показано ниже, но получил похожий вывод. Не сходится к нормальному:(. (Используя функцию ниже вместо create_bernoulli_population)
def create_uniform_population(N, Y=[]):
"""
Given the total size of population N,
this function generates list of those outcomes uniformly distributed
population list
N - Population size, eg N=10000
p - probability of interested outcome
Returns the outcomes spread out in population as a list
"""
uniform_p = 1/len(Y)
print(uniform_p)
total_pops = []
for i in range(0,len(Y)):
each_o = [i]*(int(uniform_p*N))
total_pops += each_o
shuffle(total_pops)
return total_pops
3 ответа
Можете ли вы поделиться своими настройками Matplotlib? Я думаю, что у вас есть усеченный график, вы правы в том, что выборочное распределение пропорции выборки по бернулли должно быть нормально распределено вокруг ожидаемого значения популяции...
возможно, используя что-то как:
plt.tight_layout()
проверить, нет ли проблем с графиком
def plotHist(nr, N, n_):
''' plots the RVs'''
x = np.zeros((N))
sp = f.add_subplot(3, 2, n_ )
for i in range(N):
for j in range(nr):
x[i] += np.random.binomial(10, 0.6)/10
x[i] *= 1/nr
plt.hist(x, 100, normed=True, color='#348ABD', label=" %d RVs"%(nr));
plt.setp(sp.get_yticklabels(), visible=False)
N = 1000000 # number of samples taken
nr = ([1, 2, 4, 8, 16, 32])
for i in range(np.size(nr)):
plotHist(nr[i], N, i+1)
Выше приведен пример кода, основанного на общем блоге, который я написал на CLT: https://rajeshrinet.github.io/blog/2014/central-limit-theorem/
По сути, я генерирую несколько случайных чисел (nr) из распределения в диапазоне (0,1) и суммирую их. Тогда я вижу, как они сходятся, когда я увеличиваю количество случайных чисел.
Решение:
Я думаю, что я пришел к решению. Путем обратного инжиниринга подхода Раджеша и получения подсказки от Дэниела, если график может быть проблемой, в конце концов я выяснил виновника: ширина гистограммы по умолчанию, равная 0,8, слишком широка, чтобы показать мой график сплющенным сверху. Ниже приведен модифицированный код и вывод.
from SDSP import create_bernoulli_population, get_frequency_df
from random import shuffle, choices
from bi_to_nor_demo import get_metrics, bare_minimal_plot
import matplotlib.pyplot as plt
N = 10000 # 10000 balls
p = 0.6 # probability of yellow ball is 0.6, and others (1-0.6)=>0.4
n_pickups = 10 # sample size
n_experiments = 2000 # I dont know what this is called
# THEORETICAL PDF
# generate population and calculate theoretical bernoulli pdf
population = create_bernoulli_population(N,p)
theor_df = get_frequency_df(population)
# STATISTICAL PDF
# choose sample, take mean and add to X_mean_list. Do this for n_experiments times.
X_hat = []
X_mean_list = []
for each_experiment in range(n_experiments):
X_hat = choices(population, k=n_pickups) # choose, say 10 samples from population (with replacement)
X_mean = sum(X_hat)/len(X_hat)
X_mean_list.append(X_mean)
stats_df = get_frequency_df(X_mean_list)
# plot both theoretical and statistical outcomes
fig, (ax1,ax2) = plt.subplots(2,1, figsize=(5,10))
from SDSP import plot_pdf
mu,var,sigma = get_metrics(theor_df)
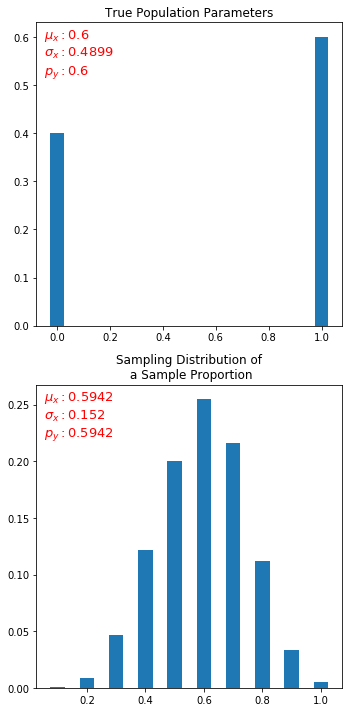
plot_pdf(theor_df, ax1, mu, sigma, p, title='True Population Parameters')
mu,var,sigma = get_metrics(stats_df)
plot_pdf(stats_df, ax2, mu, sigma, p=mu, bar_width=round(0.5/n_pickups,3),title='Sampling Distribution of\n a Sample Proportion')
plt.tight_layout()
plt.show()
Выход: