Плавное вращение с кватернионами

Question

Кватернион может описывать не только вращение, но и ориентацию, то есть вращение из начальной (нулевой) позиции.

Я хотел моделировать плавное вращение от одной ориентации к другой. Я рассчитал стартовую ориентацию startOrientation и конец ориентации endOrientation и хотел бы описать промежуточные ориентации как startOrientation*(1-argument) + endOrientation*argument в то время как argument изменения от 0 в 1,

Код для функции обновления движка обезьяны следующий:

@Override
    public void simpleUpdate(float tpf) {

        if( endOrientation != null ) {

            if( !started ) {
                started = true;
            }
            else {

                fraction += tpf * speed;
                argument = (float) ((1 - Math.cos(fraction * Math.PI)) / 2);

                orientation = startOrientation.mult(1-argument).add(endOrientation.mult(argument));
                //orientation = startOrientation.mult(1-fraction).add(endOrientation.mult(fraction));
                log.debug("tpf = {}, fraction = {}, argument = {}", tpf, fraction, argument);
                //log.debug("orientation = {}", orientation);

                rootNode.setLocalRotation(orientation);

                if( fraction >= 1 ) {

                    rootNode.setLocalRotation(endOrientation);
                    log.debug("Stopped rotating");

                    startOrientation = endOrientation = null;
                    fraction = 0;
                    started = false;
                }
            }
        }


    }

Предполагалось, что формула косинуса будет моделировать плавное ускорение в начале и замедление в конце.

Код работает, но не так, как ожидалось: плавное вращение начинается и заканчивается задолго до fraction а также argument ценности достигают 1 и я не понимаю, почему.

Почему orientation ценность достигает endOrientation так быстро?

Answer 1

Вы заявили, что в вашем случае startOrientation был изменен. Тем не мение; следующее остается верным

Интерполяция между кватернионами

Метод slerp включен в класс Quaternion для этой цели: интерполяция между двумя вращениями.

Предполагая, что у нас есть два кватерниона startOrientation а также endOrientation и мы хотим, чтобы точка interpolation между ними мы затем интерполируем, используя следующий код:

float interpolation=0.2f;
Quaternion result=new Quaternion();
result.slerp(startOrientation, endOrientation, interpolation);

Почему ваш подход может быть опасным

Кватернионы несколько сложны внутри и следуют несколько иным математическим правилам, чтобы сказать векторы. Вы назвали multiply(float scalar) метод по кватерниону. Внутренне это выглядит так

public QuaternionD mult(float scalar) {
        return new QuaternionD(scalar * x, scalar * y, scalar * z, scalar * w);
}

Так что он просто делает умножение всех элементов. Это явно не возвращает вращение, которое scalar раз размер. Фактически, такой кватернион больше не представляет действительное вращение вообще, так как он больше не единичный кватернион. Если вы позвонили normalise в этом кватерионе это немедленно отменит масштабирование. Я уверен Quaternion#multiply(float scalar) имеет некоторое применение, но я еще не нашел их.

Это также тот случай, когда "добавление" кватернионов не объединяет их. На самом деле вы умножаете их. Таким образом, объединение q1, затем q2, затем q3 будет достигнуто следующим образом:

Quaternion q0 = q1.mult(q2).mult(q3);

Шпаргалка невероятно полезна для этого

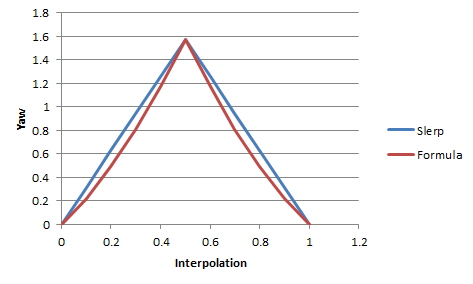
Сравнение формулы и slerp

В вашем случае ваша формула для интерполяции почти, но не совсем верна. Это показывает график рыскания для интерполяции между двумя кватернионами, используя оба метода