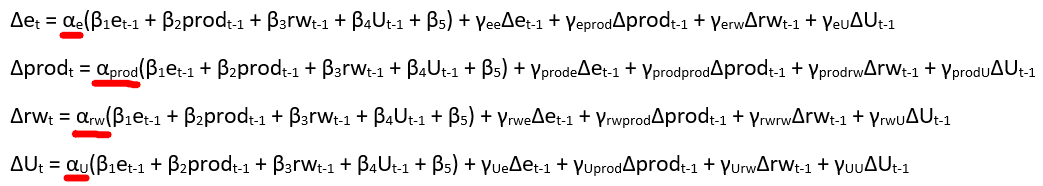VECM in R: Тестирование слабой экзогенности и наложение ограничений
Я оценил VECM и хотел бы провести 4 отдельных теста слабой экзогенности для каждой переменной.
library(urca)
library(vars)
data(Canada)
e prod rw U
1980 Q1 929.6105 405.3665 386.1361 7.53
1980 Q2 929.8040 404.6398 388.1358 7.70
1980 Q3 930.3184 403.8149 390.5401 7.47
1980 Q4 931.4277 404.2158 393.9638 7.27
1981 Q1 932.6620 405.0467 396.7647 7.37
1981 Q2 933.5509 404.4167 400.0217 7.13
...
jt = ca.jo(Canada, type = "trace", ecdet = "const", K = 2, spec = "transitory")
t = cajorls(jt, r = 1)
t$rlm$coefficients
e.d prod.d rw.d U.d
ect1 -0.005972228 0.004658649 -0.10607044 -0.02190508
e.dl1 0.812608320 -0.063226620 -0.36178542 -0.60482042
prod.dl1 0.208945048 0.275454380 -0.08418285 -0.09031236
rw.dl1 -0.045040603 0.094392696 -0.05462048 -0.01443323
U.dl1 0.218358784 -0.538972799 0.24391761 -0.16978208
t$beta
ect1
e.l1 1.00000000
prod.l1 0.08536852
rw.l1 -0.14261822
U.l1 4.28476955
constant -967.81673980
Я предполагаю, что мои уравнения:
и я хотел бы проверить, являются ли alpha_e, alpha_prod, alpha_rw, alpha_U (они отмечены красным на картинке выше) нулями и накладывают ли необходимые ограничения на мою модель. Итак, мой вопрос: как я могу это сделать?
Я предполагаю, что мои предполагаемые альфы:
e.d prod.d rw.d U.d
ect1 -0.005972228 0.004658649 -0.10607044 -0.02190508
Я предполагаю, что я должен использовать alrtest функции из урка библиотеки:
alrtest(z = jt, A = A1, r = 1)
и, вероятно, моя матрица A для alpha_e должна быть такой:
A1 = matrix(c(0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1),
nrow = 4, ncol = 3, byrow = TRUE)
Результаты теста:
jt1 = alrtest(z = jt, A = A, r = 1)
summary(jt1)
The value of the likelihood ratio test statistic:
0.48 distributed as chi square with 1 df.
The p-value of the test statistic is: 0.49
Eigenvectors, normalised to first column
of the restricted VAR:
[,1]
RK.e.l1 1.0000
RK.prod.l1 0.1352
RK.rw.l1 -0.1937
RK.U.l1 3.9760
RK.constant -960.2126
Weights W of the restricted VAR:
[,1]
[1,] 0.0000
[2,] 0.0084
[3,] -0.1342
[4,] -0.0315
Что, как я полагаю, означает, что я не могу отвергнуть свою гипотезу о слабой экзогенности alpha_e. И мои новые альфы здесь: 0,0000, 0,0084, -0,1342, -0,0315.
Теперь вопрос в том, как я могу наложить это ограничение на мою модель VECM?
Если я сделаю:
t1 = cajorls(jt1, r = 1)
t1$rlm$coefficients
e.d prod.d rw.d U.d
ect1 -0.005754775 0.007717881 -0.13282970 -0.02848404
e.dl1 0.830418381 -0.049601229 -0.30644063 -0.60236338
prod.dl1 0.207857861 0.272499006 -0.06742147 -0.08561076
rw.dl1 -0.037677197 0.102991919 -0.05986655 -0.02019326
U.dl1 0.231855899 -0.530897862 0.30720652 -0.16277775
t1$beta
ect1
e.l1 1.0000000
prod.l1 0.1351633
rw.l1 -0.1936612
U.l1 3.9759842
constant -960.2126150
у новой модели нет 0.0000, 0.0084, -0.1342, -0.0315 для альфа. Вместо этого он имеет -0,005754775 0,007717881 -0,13282970 -0,02848404.
Как я могу получить переоцененную модель с alpha_e = 0? Мне нужна переоцененная модель с alpha_e = 0, потому что я хотел бы использовать ее для прогнозов (vecm -> vec2var -> прогнозировать, но vec2var не принимает напрямую jt1). И вообще - верны ли мои расчеты или нет?
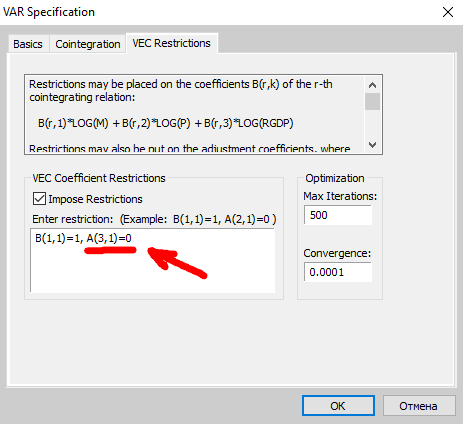
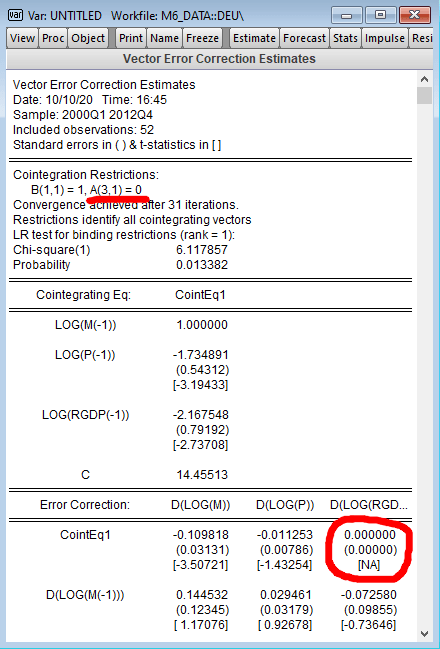
Для иллюстрации, в EViews наложение ограничения на альфа- канал выглядит так (не для этого примера):
1 ответ
If you have 1 cointegrating relationship (r=1), as it is in t = cajorls(jt, r = 1), your loading matrix can not have 4 rows and 3 columns:
A1 = matrix(c(0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1),
nrow = 4, ncol = 3, byrow = TRUE)
Matrix A can only have 4 rows and 1 column, if you have 4 variables and 1 cointegrating relationship.