Функция Auto.arima() не дает белого шума. Как еще я должен идти о моделировании данных

Question

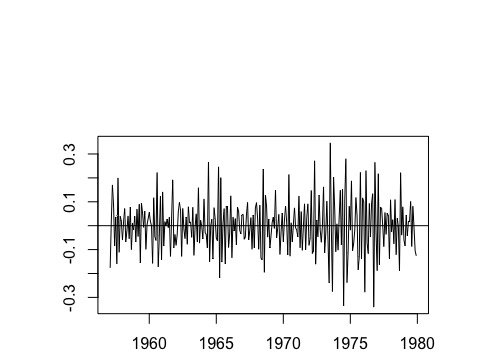
Вот график исходных данных (после выполнения преобразования журнала).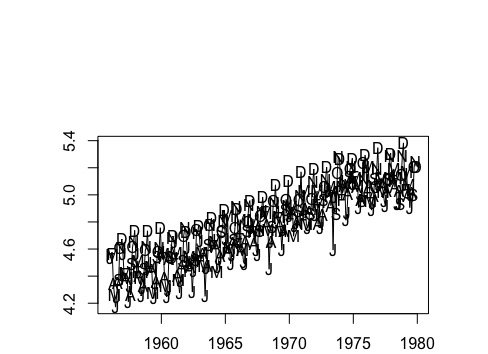

Очевидно, что существует как линейная тенденция, так и сезонная тенденция. Я могу решить оба этих вопроса, взяв первую и двенадцатую (сезонную) разницу: diff(diff(data), 12). После этого приведем график полученных данных

,

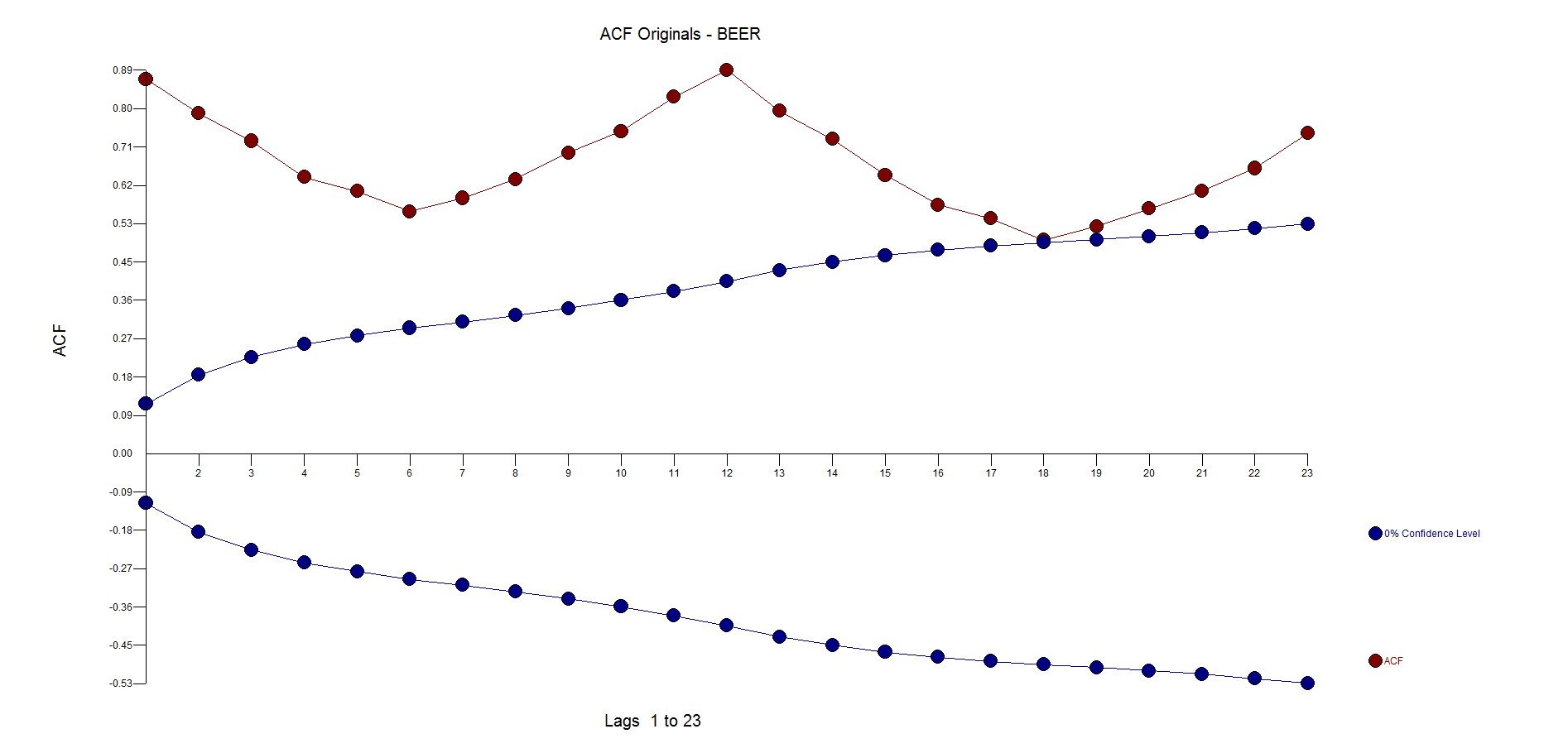
Эти данные не выглядят великолепно. Пока среднее значение постоянное, мы видим эффект воронки с течением времени. Вот ACF/PACF: ,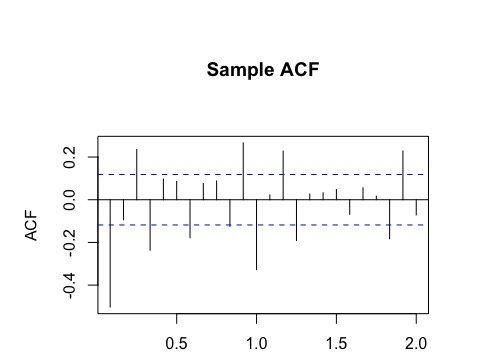

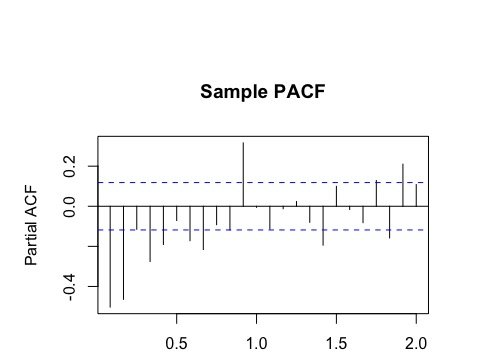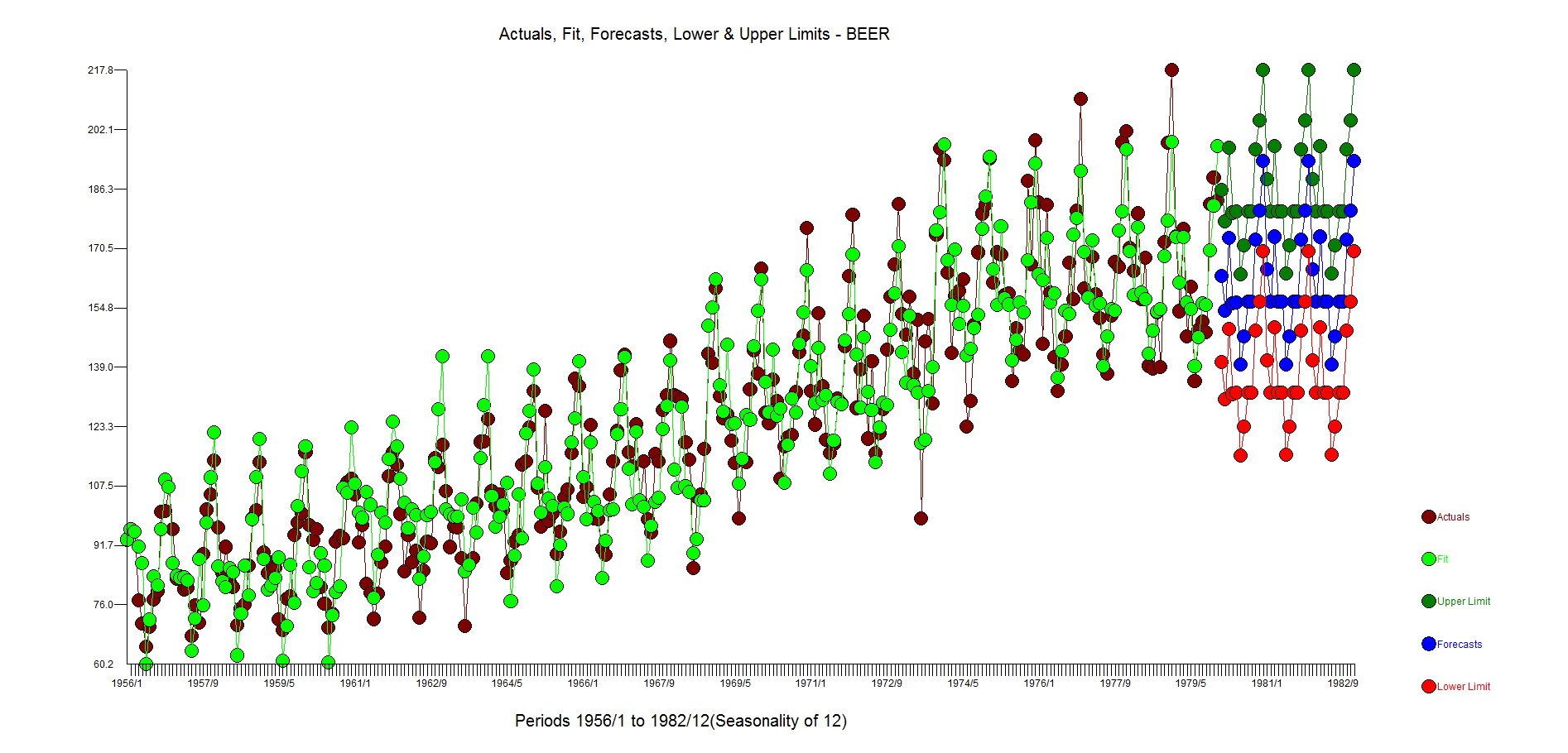
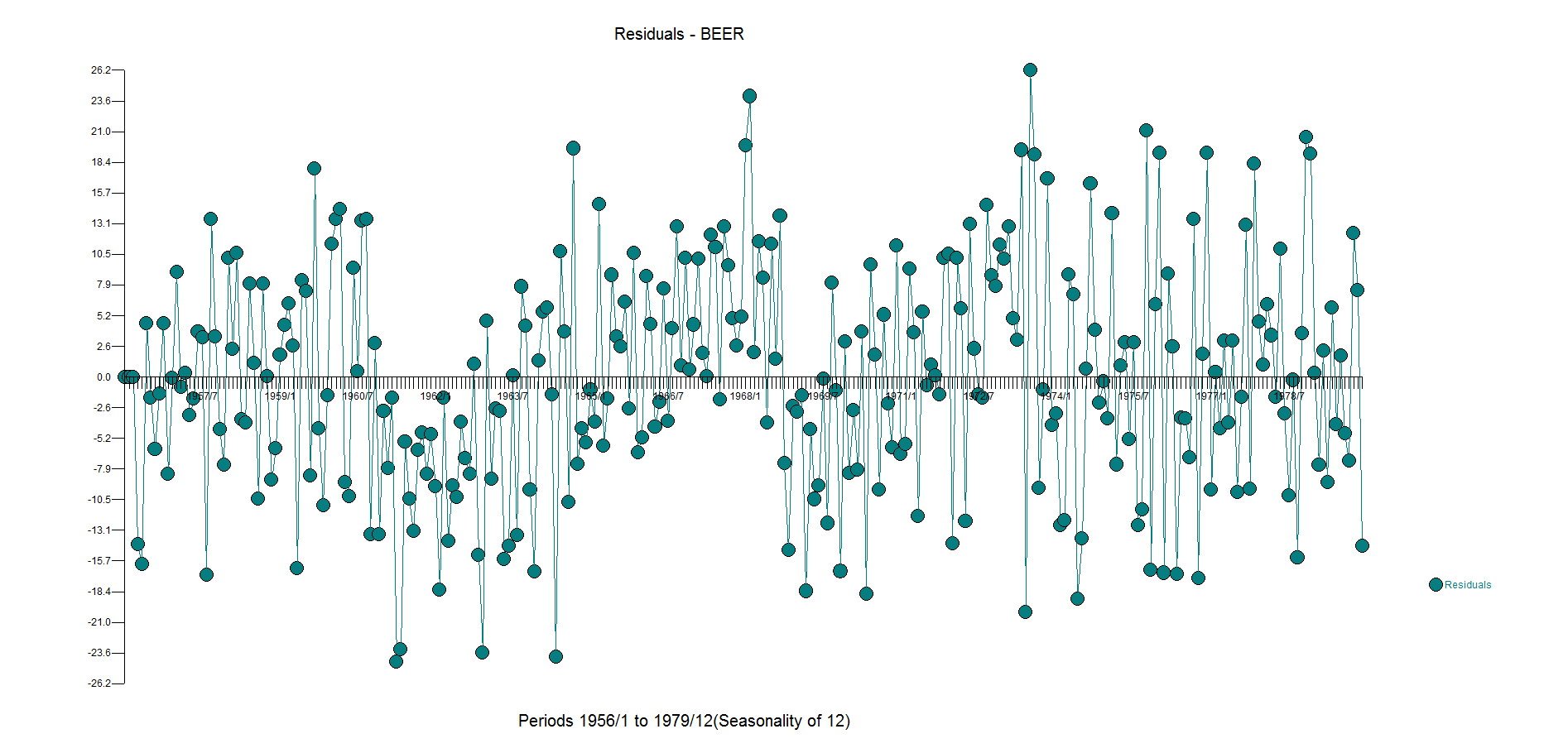
Любые предложения на возможные варианты, чтобы попробовать. Я использовал функцию auto.arima(), которая предложила модель ARIMA(2,0,2)xARIMA(1,0,2)(12). Однако, как только я взял остатки из подгонки, стало ясно, что в них все еще была какая-то структура. Вот график остатков от подгонки, а также ACF / PACF остатков.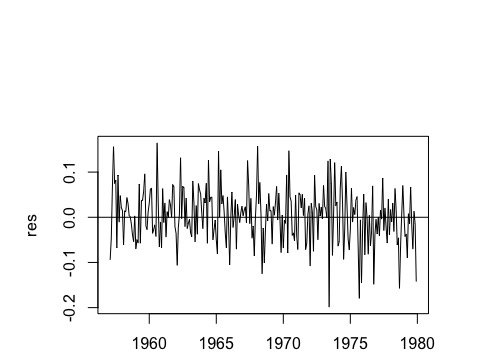

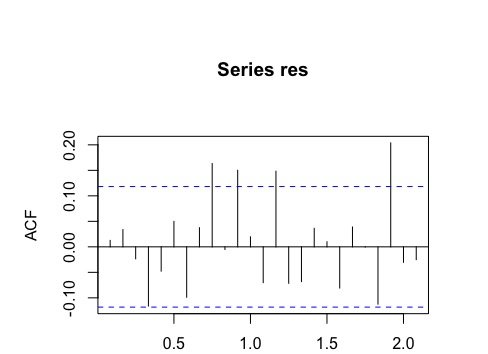
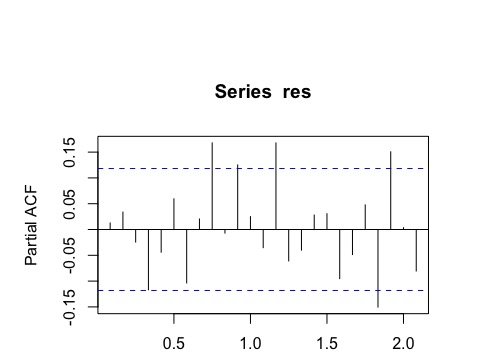
По-видимому, не существует сезонной модели, в которой лаги имеют пики в ACF / PACF остатков. Тем не менее, это все еще что-то, не охваченное предыдущими шагами. Что вы предлагаете мне сделать? Как я мог бы построить лучшую модель, которая имеет лучшую диагностику модели (которая на данный момент является просто лучше выглядящей ACF и PACF)?

Вот мой упрощенный код:

    library(TSA)
    library(forecast)
    beer <- read.csv('beer.csv', header = TRUE)
    beer <- ts(beer$Production, start = c(1956, 1), frequency = 12)

    # transform data
    boxcox <- BoxCox.ar(beer) # 0 in confidence interval
    beer.log <- log(beer)
    firstDifference <- diff(diff(beer.log), 12) # get rid of linear and 
    # seasonal trend
    acf(firstDifference)
    pacf(firstDifference)
    eacf(firstDifference)
    plot(armasubsets(firstDifference, nar=12, nma=12))

    # fitting the model
    auto.arima(firstDifference, ic = 'bic') # from forecasting package
    modelFit <- arima(firstDifference, order=c(1,0,0),seasonal
    =list(order=c(2, 0, 0), period = 12))

    # assessing model
    resid <- modelFit$residuals                     
    acf(resid, lag.max = 15)
    pacf(resid, lag.max = 15)

Вот данные, если вы заинтересованы (я думаю, что вы можете использовать конвертер html в csv, если хотите): https://docs.google.com/spreadsheets/d/1S8BbNBdQFpQAiCA4J18bf7PITb8kfThorMENW-FRvW4/pubhtml

Answer 1

Джейн,

Здесь происходит несколько вещей.

Вместо бревен мы использовали тест дисперсии Цай, который показывает, что дисперсия увеличилась после периода 118. С этим справляется взвешенный метод наименьших квадратов.

Март становится выше, начиная с периода 111. Альтернативой ar12 или сезонной разницей является выявление сезонных манекенов. Мы обнаружили, что 7 из 12 месяцев были необычными со сдвигом пары уровней, AR2 с 2 выбросами.

Вот подгонка и прогнозы.

Вот остатки.

АКФ остатков

Примечание: я являюсь разработчиком программного обеспечения Autobox. Все модели не правы. Некоторые полезны.

Вот статья Цая http://onlinelibrary.wiley.com/doi/10.1002/for.3980070102/abstract