3-осевое кватернионное вращение в OpenGL

Question

Я пытаюсь создать программу OpenGL, в которой модель птицы должна следовать определенному пути вдоль поверхности сферы, описанной сферической спиралью Зейфферта. Тем не менее, я застрял на правильном вращении в течение достаточно долгого времени.

В качестве первого шага я заставляю птицу следовать по круговому пути в плоскости xz:

// 1. Circle in x-z plane
float phi =  TWO_PI * t; // t = [0..1]

float x = boundingSphereRadius * cos(phi);
float y = 0.0f;
float z = boundingSphereRadius * sin(phi);

float rotationAngle = glm::orientedAngle(glm::vec3(0.0f, 0.0f, 1.0f),    
                                         glm::normalize(glm::vec3(x, 0, z)),
                                         glm::vec3(0.0f, 1.0f, 0.0f)) - HALF_PI;
glm::fquat rotation = glm::angleAxis(rotationAngle, glm::vec3(0.0f, 1.0f, 0.0f));

Фиксированный -HALF_PI необходимо, чтобы птица была правильно выровнена. Это прекрасно работает, и аналогичным образом я могу добиться кругового вращения в плоскости xy и yz.

Проблема возникает, когда я пытаюсь накопить все различные вращения. Путь, по которому я пытаюсь следовать, выглядит так:

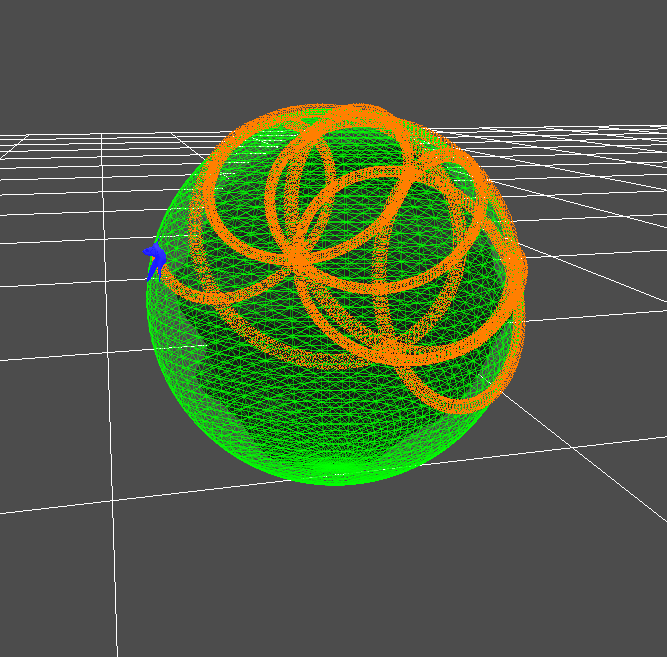
По требованию живот птицы всегда должен быть обращен к поверхности сферы, а птица должна лететь вперед.

Мой нынешний подход выглядит следующим образом: он состоит из простого объединения трех кватернионов ориентации:

glm::fquat rotationX  = glm::angleAxis(glm::orientedAngle(glm::normalize(glm::vec3(0.0f, 0.0f, 1.0f)), glm::normalize(glm::vec3(x, 0, z)), glm::vec3(0.0f, 1.0f, 0.0f)) - HALF_PI, glm::vec3(0.0f, 1.0f, 0.0f));
glm::fquat rotationY1 = glm::angleAxis(-HALF_PI, glm::vec3(0.0f, 1.0f, 0.0f));
glm::fquat rotationY2 = glm::angleAxis(glm::orientedAngle(glm::vec3(0.0f, 1.0f, 0.0f), glm::normalize(glm::vec3(x, y, 0)), glm::vec3(0.0f, 0.0f, 1.0f)), glm::vec3(0.0f, 0.0f, 1.0f));
glm::fquat rotationY  = rotationY2 * rotationY1;
glm::fquat rotationZ  = glm::angleAxis(glm::orientedAngle(glm::vec3(0.0f, 0.0f, 1.0f), glm::normalize(glm::vec3(0, y, z)), glm::vec3(1.0f, 0.0f, 0.0f)) + HALF_PI, glm::vec3(1.0f, 0.0f, 0.0f));
glm::fquat rotation   = rotationZ * rotationY * rotationX;

Однако изменения ориентации совершенно неверны, и под некоторыми углами происходят скачки.

РЕДАКТИРОВАТЬ:

Сейчас я пробую разные круги на сфере, где необходимо более одного вращения. За beta = gamma = 0.0f а также alpha = HALF_PI круг снова в плоскости XZ и значение rotationAngleXZ меняется, в то время как rotationAngleXY либо -HALF_PI из HALF_PI а также rotationAngleYZ либо 0.0f или же PI, Я предполагаю, что сталкиваюсь здесь с замком карданного подвеса и прочитал множество статей об этом, однако я все еще не уверен, как я могу предотвратить это в этом случае.

// 10. `Arbitrary` circles on sphere surface
// http://math.stackexchange.com/questions/643130/circle-on-sphere
//
// Parameters:
//      alpha = 0...HALF_PI - For alpha = 0, the circle is just a point - For alpha = HALF_PI, the circle is a Great Circle
//      (beta, gamma) = center of circle in spherical coordinates
float phi =  TWO_PI * t;

float x = boundingSphereRadius * ( (sin(alpha) * cos(beta) * cos(gamma)) * cos(phi) + (sin(alpha) * sin(gamma)) * sin(phi) - (cos(alpha) * sin(beta) * cos(gamma)));
float y = boundingSphereRadius * ( (sin(alpha) * sin(beta)) * cos(phi) + cos(alpha) * cos(beta));
float z = boundingSphereRadius * (-(sin(alpha) * cos(beta) * sin(gamma)) * cos(phi) + (sin(alpha) * cos(gamma)) * sin(phi) + (cos(alpha) * sin(beta) * sin(gamma)));

float rotationAngleXZ = glm::orientedAngle(glm::normalize(glm::vec3(0.0f, 0.0f, 1.0f)), glm::normalize(glm::vec3(x, 0, z)), glm::vec3(0.0f, 1.0f, 0.0f));
std::cout << "Rotation Angle XZ = " << rotationAngleXZ << std::endl;
glm::fquat rotationXZ = glm::angleAxis(rotationAngleXZ - HALF_PI, glm::vec3(0.0f, 1.0f, 0.0f));

float rotationAngleXY = glm::orientedAngle(glm::vec3(0.0f, 1.0f, 0.0f), glm::normalize(glm::vec3(x, y, 0)), glm::vec3(0.0f, 0.0f, 1.0f));
std::cout << "Rotation Angle XY = " << rotationAngleXY << std::endl;
glm::fquat rotationXY_Y = glm::angleAxis(-HALF_PI, glm::vec3(0.0f, 1.0f, 0.0f));
glm::fquat rotationXY_Z = glm::angleAxis(rotationAngleXY, glm::vec3(0.0f, 0.0f, 1.0f));
glm::fquat rotationXY = rotationXY_Z * rotationXY_Y;

float rotationAngleYZ = glm::orientedAngle(glm::vec3(0.0f, 0.0f, 1.0f), glm::normalize(glm::vec3(0, y, z)), glm::vec3(1.0f, 0.0f, 0.0f));
std::cout << "Rotation Angle YZ = " << rotationAngleYZ << std::endl;
glm::fquat rotationYZ = glm::angleAxis(rotationAngleYZ + HALF_PI, glm::vec3(1.0f, 0.0f, 0.0f));

glm::fquat rotation = glm::normalize(rotationXZ) * glm::normalize(rotationXY) * glm::normalize(rotationYZ);

Answer 1

Ваш код использует углы Эйлера (вращение по оси). Шатания и скачки объясняются тем, что углы Эйлера являются плохой параметризацией пространства трехмерных вращений. Вместо этого здесь есть два альтернативных подхода.

Построение матрицы вращения через рамку

Предполагая, что птица указывает вниз по оси X и вверх в своей локальной системе координат.

Позволять p = [x y z] быть в положении птицы. Пусть v будет его вектором скорости. Позволять

f = v/|v|
up = p/|p|
s = cross(f, up)

Теперь построим матрицу со строками f, up, s. В частности:

[  f[0]   f[1]  f[2] ]
[ up[0]  up[1] up[2] ]
[  s[0]   s[1]  s[2] ]

Затем сгенерируйте кватернион через GLM quat_cast функция.

Избегайте gluLookAt, потому что он использует устаревший стек матрицы фиксированных функций.

Наращивание с помощью поворотов (кватернионов)

Позволять R0 быть вращение от i в f, (Угол acos(dot(i,f)) и ось cross(i,f))

Позволять R1 быть вращение от R0*j в up, (Использование матричного умножения, поскольку в этом контексте это проще)

Позволять R2 быть вращение от R1*R0*k в s,

Финальный поворот должен быть R2*R1*R0, Убедитесь, что это вращение равно матрице выше.

Answer 2

У меня нет готового кода для вас, но как насчет этой идеи? Предполагая, что у вас уже есть формула для местоположения птицы по x,y,z как функции от t (сферическая спираль Зейфферта). Затем:

eye    = fn(t)
center = fn(t + dt) // where will the bird be in the next time-step
up     = normalize(eye - sphereCenter)

Теперь gluLookAt(глаз, центр, вверх) предоставит матрицу, и вы сможете использовать ее для ориентации своей птицы.

Эта ссылка также может помочь: https://gamedev.stackexchange.com/questions/41940/how-does-glulookat-work.

Надеюсь это поможет,

--Роджер