Прогноз временных рядов - ARIMA/ARIMAX с ежедневными данными в R
enter code here Я работаю над проектом по анализу и прогнозированию временных рядов продаж и доходов клиента. Существуют различные модели, которые я хочу протестировать для целей точности, а именно: линейный метод Холта, метод Зимнего Холта, ARIMA, сезонная ARIMA и ARIMAX (поскольку я также хочу учитывать категориальные переменные в данных). Данные представлены в ежедневной форме, и поэтому я выбрал частоту 7.
startW <- as.numeric(strftime(head(revenue$date, 1), format = "%W"))
startD <- as.numeric(strftime(head(revenue$date, 1) + 1, format =" %w"))
revenue <- ts(revenue$amount, start = c(startW, startD), frequency = 7)
Затем я разделил его на тренировку и тестирование, сохранив прошлый месяц в качестве удержания.
я использовал auto.arima() функция для модели ARIMA и дает ARIMA(0,0,0)(2,1,0)[7]. Что это значит? График остатков выглядит следующим образом
После этого я добавил праздники в качестве внешней переменной
encoded_regressors <- sparse.model.matrix(amount~holiday, data = train_set)
encoded_regressors <- (encoded_regressors[,-1])
model2 <- auto.arima(revenue.train, xreg = encoded_regressors)
Модель, которую я сейчас получаю, - ARIMA(0,0,1)(2,1,0)[7], а здесь - остаточный график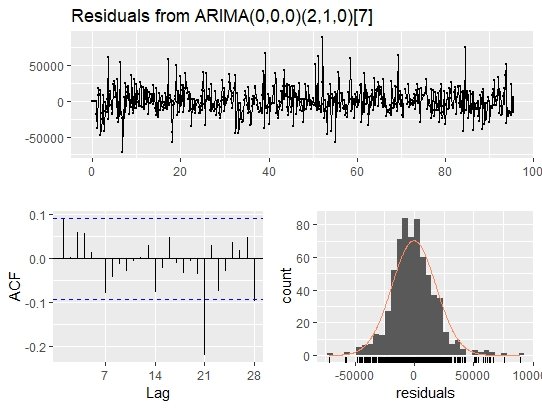 
,
Для обоих случаев, если я вижу разницу в прогнозируемом и наблюдаемом значении, процентная разница колеблется в среднем от 3% до 50%. Как я могу улучшить свою модель и понять результаты модели ARIMA?
Спасибо!
2 ответа
Вы, кажется, используете auto.arima() от forecast пакет. Вы можете найти много полезной информации об использовании этого пакета и прогнозировании временных рядов в R здесь. Для вывода, который вы дали, 3 значения в первых скобках относятся к порядку p, d и q в модели ARIMA. p - авторегрессионный член, d - порядок разности, а q - член скользящей средней. 3 значения во вторых скобках относятся к сезонным компонентам P, D и Q, причем каждое из них относится к терминам авторегрессии, дифференцирования и скользящего среднего соответственно. Число 7 в скобках относится к выбранной вами частоте.
В общем, чтобы найти лучшую модель ARIMA, вы должны взглянуть на Информационный критерий Акаике (AIC) или Байесовский информационный критерий (BIC) и попытаться свести их к минимуму. Опять же, посмотрите на ссылку для более подробной информации.
Графики ACF и PACF временных рядов соответствуют 
Если мое понимание верно, ACF предлагает q = 7, а PACF предлагает p = 7?