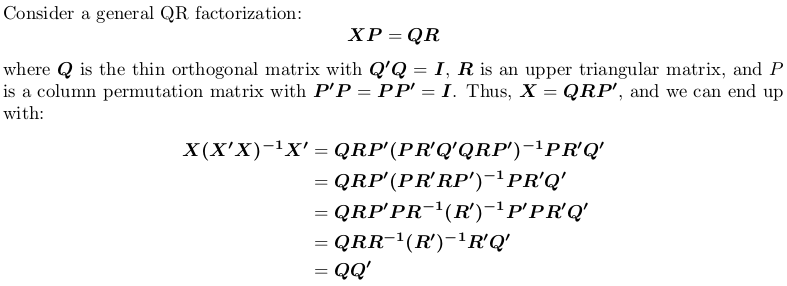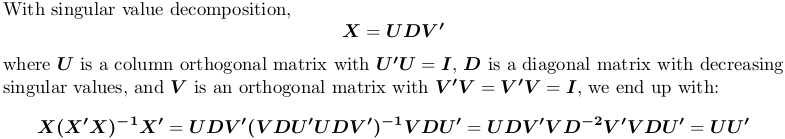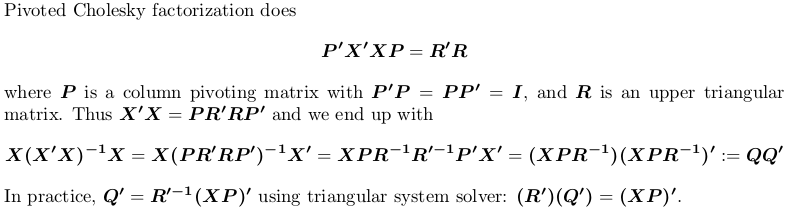Вычислить матрицу проекции / шапки с помощью QR-факторизации, SVD (и факторизации Холецкого?)
Я пытаюсь вычислить в R матрицу проекции P произвольной матрицы N x J S:
P = S (S'S) ^ -1 S'
Я пытался выполнить это с помощью следующей функции:
P <- function(S){
output <- S %*% solve(t(S) %*% S) %*% t(S)
return(output)
}
Но когда я использую это, я получаю ошибки, которые выглядят так:
# Error in solve.default(t(S) %*% S, t(S), tol = 1e-07) :
# system is computationally singular: reciprocal condition number = 2.26005e-28
Я думаю, что это результат недостатка чисел и / или нестабильности, о чем говорилось во многих местах, таких как r-help и здесь, но я недостаточно опытен в использовании SVD или QR-декомпозиции, чтобы решить проблему, или же поместить этот существующий код в действие. Я также попробовал предложенный код, который должен написать решит как система:
output <- S %*% solve (t(S) %*% S, t(S), tol=1e-7)
Но все равно это не работает. Мы ценим любые предложения.
Я почти уверен, что моя матрица должна быть обратимой и не иметь какой-либо коллинеарности хотя бы потому, что я пытался проверить это с помощью матрицы ортогональных фиктивных переменных, и она все еще не работает.
Кроме того, я хотел бы применить это к довольно большим матрицам, поэтому я ищу аккуратное общее решение.
1 ответ
Хотя ОП не был активен более года, я все же решил опубликовать ответ. я хотел бы использовать X вместо SКак и в статистике, нам часто требуется проекционная матрица в контексте линейной регрессии, где X это матрица модели, y вектор ответа, в то время как H = X(X'X)^{-1}X' это шляпа / матрица проекции, так что Hy дает прогнозные значения.
Этот ответ предполагает контекст обычных наименьших квадратов. Для взвешенных наименьших квадратов см. Раздел Получение матрицы шапки из разложения QR для взвешенной регрессии наименьших квадратов.
Обзор
solve основан на факторизации LU общей квадратной матрицы. За X'X (должно быть вычислено crossprod(X) скорее, чем t(X) %*% X в R читайте ?crossprod для более), который является симметричным, мы можем использовать chol2inv которая основана на холексовой факторизации.
Тем не менее, треугольная факторизация менее стабильна, чем QR факторизации. Это не сложно понять. Если X имеет условный номер kappa, X'X будет иметь условный номер kappa ^ 2, Это может вызвать большие численные трудности. Сообщение об ошибке вы получите:
# system is computationally singular: reciprocal condition number = 2.26005e-28
просто говорит это. kappa ^ 2 около e-28намного меньше точности станка e-16, С толерантностью tol = .Machine$double.eps, X'X будет считаться рангом дефицитным, поэтому факторизация ЛУ и Холецкого будет нарушена.
Как правило, мы переключаемся на SVD или QR в этой ситуации, но поворотная холеризация факторизации является другим выбором.
- СВД - самый стабильный метод, но слишком дорогой;
- QR удовлетворительно стабилен, при умеренных вычислительных затратах и широко используется на практике;
- Поворотный Холецкий быстр, с приемлемой стабильностью. Для большой матрицы этот предпочтителен.
Далее я объясню все три метода.
Использование QR-факторизации
Обратите внимание, что матрица проекции не зависит от перестановки, т. Е. Не имеет значения, выполняем ли мы факторизацию QR с поворотом или без него.
В R, qr.default можно вызвать процедуру LINPACK DQRDC для неповоротной QR-факторизации и рутины LAPACK DGEQP3 для блочной поворотной QR-факторизации. Давайте сгенерируем игрушечную матрицу и протестируем оба варианта:
set.seed(0); X <- matrix(rnorm(50), 10, 5)
qr_linpack <- qr.default(X)
qr_lapack <- qr.default(X, LAPACK = TRUE)
str(qr_linpack)
# List of 4
# $ qr : num [1:10, 1:5] -3.79 -0.0861 0.3509 0.3357 0.1094 ...
# $ rank : int 5
# $ qraux: num [1:5] 1.33 1.37 1.03 1.01 1.15
# $ pivot: int [1:5] 1 2 3 4 5
# - attr(*, "class")= chr "qr"
str(qr_lapack)
# List of 4
# $ qr : num [1:10, 1:5] -3.79 -0.0646 0.2632 0.2518 0.0821 ...
# $ rank : int 5
# $ qraux: num [1:5] 1.33 1.21 1.56 1.36 1.09
# $ pivot: int [1:5] 1 5 2 4 3
# - attr(*, "useLAPACK")= logi TRUE
# - attr(*, "class")= chr "qr"
Обратите внимание $pivot отличается для двух объектов.
Теперь мы определяем функцию-оболочку для вычисления QQ':
f <- function (QR) {
## thin Q-factor
Q <- qr.qy(QR, diag(1, nrow = nrow(QR$qr), ncol = QR$rank))
## QQ'
tcrossprod(Q)
}
Мы увидим что qr_linpack а также qr_lapack дать ту же матрицу проекции:
H1 <- f(qr_linpack)
H2 <- f(qr_lapack)
mean(abs(H1 - H2))
# [1] 9.530571e-17
Использование разложения по сингулярным числам
В R, svd вычисляет разложение по сингулярным числам. Мы все еще используем приведенный выше пример матрицы X:
SVD <- svd(X)
str(SVD)
# List of 3
# $ d: num [1:5] 4.321 3.667 2.158 1.904 0.876
# $ u: num [1:10, 1:5] -0.4108 -0.0646 -0.2643 -0.1734 0.1007 ...
# $ v: num [1:5, 1:5] -0.766 0.164 0.176 0.383 -0.457 ...
H3 <- tcrossprod(SVD$u)
mean(abs(H1 - H3))
# [1] 1.311668e-16
Опять же, мы получаем ту же матрицу проекции.
Использование Pivoted-факторизации Холецкого
Для демонстрации мы все еще используем пример X выше.
## pivoted Chol for `X'X`; we want lower triangular factor `L = R'`:
## we also suppress possible rank-deficient warnings (no harm at all!)
L <- t(suppressWarnings(chol(crossprod(X), pivot = TRUE)))
str(L)
# num [1:5, 1:5] 3.79 0.552 -0.82 -1.179 -0.182 ...
# - attr(*, "pivot")= int [1:5] 1 5 2 4 3
# - attr(*, "rank")= int 5
## compute `Q'`
r <- attr(L, "rank")
piv <- attr(L, "pivot")
Qt <- forwardsolve(L, t(X[, piv]), r)
## P = QQ'
H4 <- crossprod(Qt)
## compare
mean(abs(H1 - H4))
# [1] 6.983997e-17
Опять же, мы получаем ту же матрицу проекции.
Как насчет подачи заявления chol в S'S, затем chol2inv, Должно быть более стабильным:
chol2inv(chol(crossprod(S)))