Получить матрицу шапки из разложения QR для взвешенной регрессии наименьших квадратов

Question

Я пытаюсь продлить lwr() функция пакета McSptial, что соответствует взвешенным регрессиям как непараметрическая оценка. В основе lwr() функция, она инвертирует матрицу, используя solve() вместо разложения QR, что приводит к численной нестабильности. Я хотел бы изменить это, но не могу понять, как получить матрицу шляпы (или другие производные) из разложения QR впоследствии.

С данными:

set.seed(0); xmat <- matrix(rnorm(500), nrow=50)    ## model matrix
y <- rowSums(rep(2:11,each=50)*xmat)    ## arbitrary values to let `lm.wfit` work
w <- runif(50, 1, 2)    ## weights

lwr() Функция работает следующим образом:

xmat2 <- w * xmat
xx <- solve(crossprod(xmat, xmat2))
xmat1 <- tcrossprod(xx, xmat2)
vmat <- tcrossprod(xmat1)

Мне нужно значение, например:

sum((xmat[1,] %*% xmat1)^2)
sqrt(diag(vmat))

На данный момент я использую reg <- lm.wfit(x=xmat, y=y, w=w) но не могу вернуть то, что мне кажется шляпной матрицей (xmat1) из этого.

Answer 1

Этот старый вопрос является продолжением другого старого вопроса, на который я только что ответил: вычислить матрицу проекции / шляпы с помощью QR-факторизации, SVD (и факторизации Холецкого?). В этом ответе обсуждаются 3 варианта вычисления матрицы шляп для обычной задачи наименьших квадратов, в то время как этот вопрос находится в контексте взвешенных наименьших квадратов. Но результат и метод в этом ответе будут основой моего ответа здесь. В частности, я только продемонстрирую подход QR.

ОП упомянул, что мы можем использовать lm.wfit вычислить QR-факторизацию, но мы могли бы сделать это, используя qr.default мы сами, это то, как я покажу.

---

Прежде чем продолжить, я должен указать, что код OP не делает то, что он думает. xmat1 это не шляпная матрица; вместо, xmat %*% xmat1 является. vmat это не шляпная матрица, хотя я не знаю, что это на самом деле. Тогда я не понимаю, что это:

sum((xmat[1,] %*% xmat1)^2)
sqrt(diag(vmat))

Второй выглядит как диагональ шляпной матрицы, но, как я уже сказал, vmat это не шляпная матрица. Ну, во всяком случае, я продолжу правильное вычисление для шляпной матрицы и покажу, как получить ее диагональ и трассировку.

---

Рассмотрим игрушечную модель матрицы X и некоторые однородные, положительные веса w:

set.seed(0); X <- matrix(rnorm(500), nrow = 50)
w <- runif(50, 1, 2)    ## weights must be positive
rw <- sqrt(w)    ## square root of weights

Сначала мы получаем X1 (X_tilde в латексном абзаце) путем изменения масштаба строки до X:

X1 <- rw * X

Затем мы выполняем QR-факторизацию для X1, Как обсуждалось в моем связанном ответе, мы можем выполнить эту факторизацию с поворотом столбца или без него. lm.fit или же lm.wfit следовательно lm не делает поворот, но здесь я буду использовать поворотную факторизацию в качестве демонстрации.

QR <- qr.default(X1, LAPACK = TRUE)
Q <- qr.qy(QR, diag(1, nrow = nrow(QR$qr), ncol = QR$rank))

Обратите внимание, мы не пошли на вычисления tcrossprod(Q) как в связанном ответе, потому что это для обычных наименьших квадратов. Для взвешенных наименьших квадратов мы хотим Q1 а также Q2:

Q1 <- (1 / rw) * Q
Q2 <- rw * Q

Если нам нужна только диагональ и трассировка матрицы шляп, нет необходимости выполнять матричное умножение, чтобы сначала получить полную матрицу шляп. Мы можем использовать

d <- rowSums(Q1 * Q2)  ## diagonal
# [1] 0.20597777 0.26700833 0.30503459 0.30633288 0.22246789 0.27171651
# [7] 0.06649743 0.20170817 0.16522568 0.39758645 0.17464352 0.16496177
#[13] 0.34872929 0.20523690 0.22071444 0.24328554 0.32374295 0.17190937
#[19] 0.12124379 0.18590593 0.13227048 0.10935003 0.09495233 0.08295841
#[25] 0.22041164 0.18057077 0.24191875 0.26059064 0.16263735 0.24078776
#[31] 0.29575555 0.16053372 0.11833039 0.08597747 0.14431659 0.21979791
#[37] 0.16392561 0.26856497 0.26675058 0.13254903 0.26514759 0.18343306
#[43] 0.20267675 0.12329997 0.30294287 0.18650840 0.17514183 0.21875637
#[49] 0.05702440 0.13218959

edf <- sum(d)  ## trace, sum of diagonals
# [1] 10

В линейной регрессии, d является влияние каждого элемента, и это полезно для получения доверительного интервала (используя sqrt(d)) и стандартизированные остатки (с использованием sqrt(1 - d)). След, это эффективное число параметров или эффективная степень свободы для модели (поэтому я называю это edf). Мы видим, что edf = 10, потому что мы использовали 10 параметров: X имеет 10 столбцов, и это не ранг-дефицит.

Обычно d а также edf это все, что нам нужно. В редких случаях нам нужна полная матрица шляп. Чтобы получить его, нам нужно дорогое матричное умножение:

H <- tcrossprod(Q1, Q2)

---

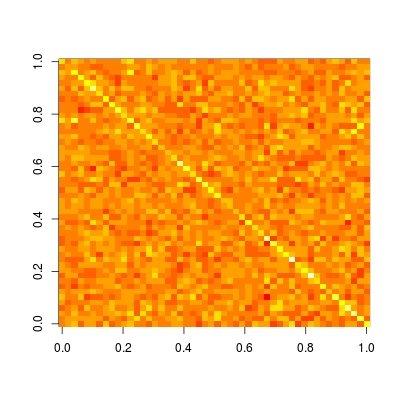
Шляпная матрица особенно полезна для того, чтобы помочь нам понять, является ли модель локальной / редкой или нет. Давайте построим эту матрицу (читать ?image подробности и примеры того, как построить матрицу в правильной ориентации):

image(t(H)[ncol(H):1,])

Мы видим, что эта матрица полностью плотна. Это означает, что прогноз на каждом уровне зависит от всех данных, т. Е. Прогноз не является локальным. В то время как если мы сравним с другими непараметрическими методами прогнозирования, такими как регрессия ядра, лесс, P-сплайн (регрессия оштрафованного B-сплайна) и вейвлет, мы увидим разреженную матрицу шапки. Поэтому эти методы известны как локальная подгонка.