Построение эффектов взаимодействия в байесовских моделях (с использованием rstanarm)

Question

Я пытаюсь показать, как влияние одной переменной изменяется со значениями другой переменной в байесовской линейной модели в rstanarm(). Я могу подобрать модель и взять результаты из апостериора, чтобы посмотреть на оценки для каждого параметра, но не ясно, как дать какой-то график зависимости одной переменной во взаимодействии при изменении других и связанной с этим неопределенности. (то есть участок предельных эффектов). Ниже моя попытка:

library(rstanarm)

# Set Seed
set.seed(1)

# Generate fake data
w1 <- rbeta(n = 50, shape1 = 2, shape2 = 1.5)
w2 <- rbeta(n = 50, shape1 = 3, shape2 = 2.5)

dat <- data.frame(y = log(w1 / (1-w1)),
                  x = log(w2 / (1-w2)),
                  z = seq(1:50))

# Fit linear regression without an intercept:
m1 <- rstanarm::stan_glm(y ~ 0 + x*z, 
                         data = dat,
                         family = gaussian(),
                         algorithm = "sampling",
                         chains = 4,
                         seed = 123,
                         )


# Create data sets with low values and high values of one of the predictors
dat_lowx <- dat
dat_lowx$x <- 0

dat_highx <- dat
dat_highx$x <- 5

out_low <- rstanarm::posterior_predict(object = m1,
                                   newdata = dat_lowx)

out_high <- rstanarm::posterior_predict(object = m1,
                                        newdata = dat_highx)

# Calculate differences in posterior predictions
mfx <- out_high - out_low

# Somehow get the coefficients for the other predictor?

Answer 1

В этом (линейном, гауссовском, тождественном, без перехвата) случае,

mu = beta_x * x + beta_z * z + beta_xz * x * z 
   = (beta_x + beta_xz * z) * x 
   = (beta_z + beta_xz * x) * z

Итак, чтобы построить предельный эффект x или же zвам просто нужен соответствующий диапазон каждого и апостериорного распределения коэффициентов, которые вы можете получить через

post <- as.data.frame(m1)

затем

dmu_dx <- post[ , 1] + post[ , 3] %*% t(sort(dat$z))
dmu_dz <- post[ , 2] + post[ , 3] %*% t(sort(dat$x))

И затем вы можете оценить один предельный эффект для каждого наблюдения в ваших данных, используя что-то вроде ниже, который рассчитал эффект x на mu для каждого наблюдения в ваших данных и эффекта z на mu за каждое наблюдение.

colnames(dmu_dx) <- round(sort(dat$x), digits = 1)
colnames(dmu_dz) <- dat$z
bayesplot::mcmc_intervals(dmu_dz)
bayesplot::mcmc_intervals(dmu_dx)

Обратите внимание, что имена столбцов в данном случае являются просто наблюдениями.

Answer 2

Вы также можете использовать любой пакет ggeffects, особенно для маргинальных эффектов; или sjPlot-пакет для маргинальных эффектов и других типов графиков (для маржинальных эффектов sjPlot просто оборачивает функции из ggeffects).

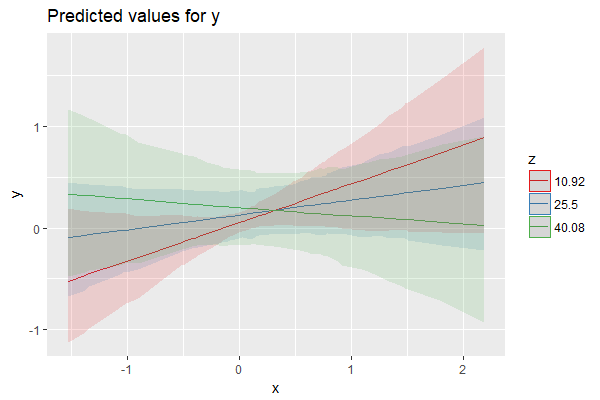
Для построения предельных эффектов взаимодействий используйте sjPlot::plot_model() с type = "int", использование mdrt.values определить, какие значения построить для непрерывных переменных модератора, и использовать ppd чтобы прогнозирование основывалось либо на апостериорном распределении линейного предиктора, либо на основе апостериорного прогнозирующего распределения.

library(sjPlot)
plot_model(m1, type = "int", terms = c("x", "z"), mdrt.values = "meansd")

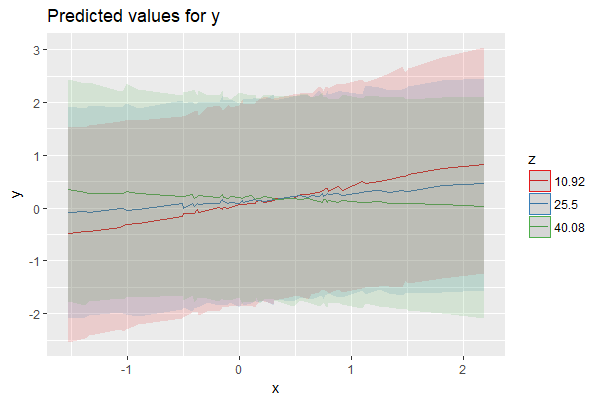
plot_model(m1, type = "int", terms = c("x", "z"), mdrt.values = "meansd", ppd = TRUE)

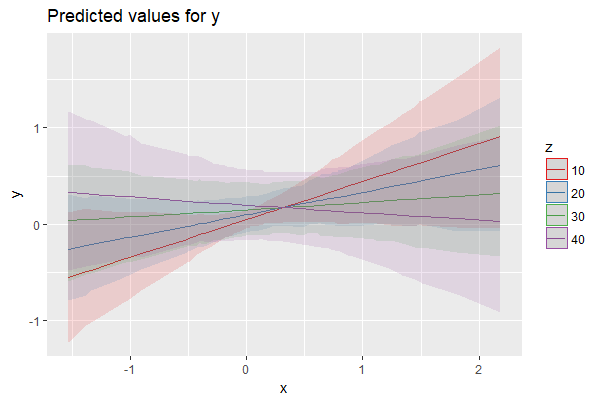
или для нанесения предельных эффектов на другие конкретные значения, используйте type = "pred" и укажите значения в terms -argument:

plot_model(m1, type = "pred", terms = c("x", "z [10, 20, 30, 40]"))
# same as:
library(ggeffects)
dat <- ggpredict(m1, terms = c("x", "z [10, 20, 30, 40]"))
plot(dat)

Есть больше вариантов, а также различные способы настройки внешнего вида сюжета. См. Связанные файлы справки и виньетки пакетов.