Подгонка замкнутой кривой к набору точек
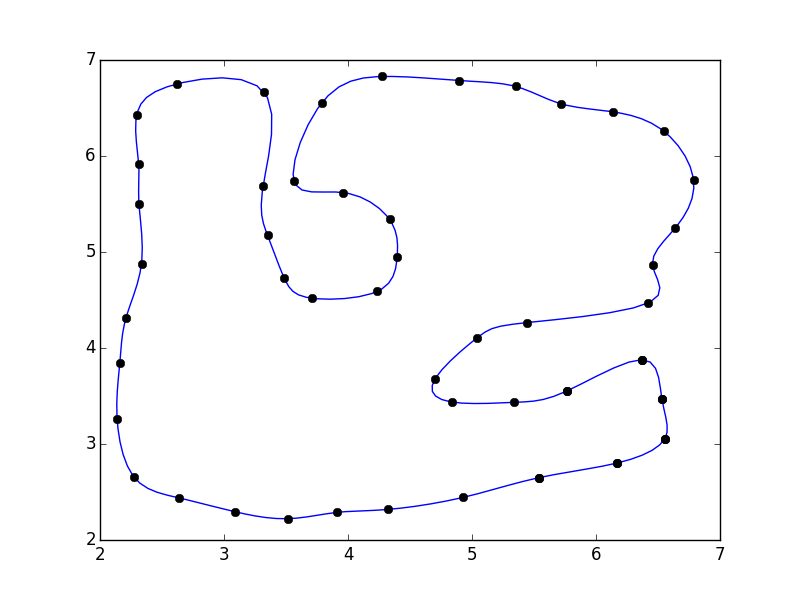
У меня есть набор очков pts которые образуют цикл, и это выглядит так:
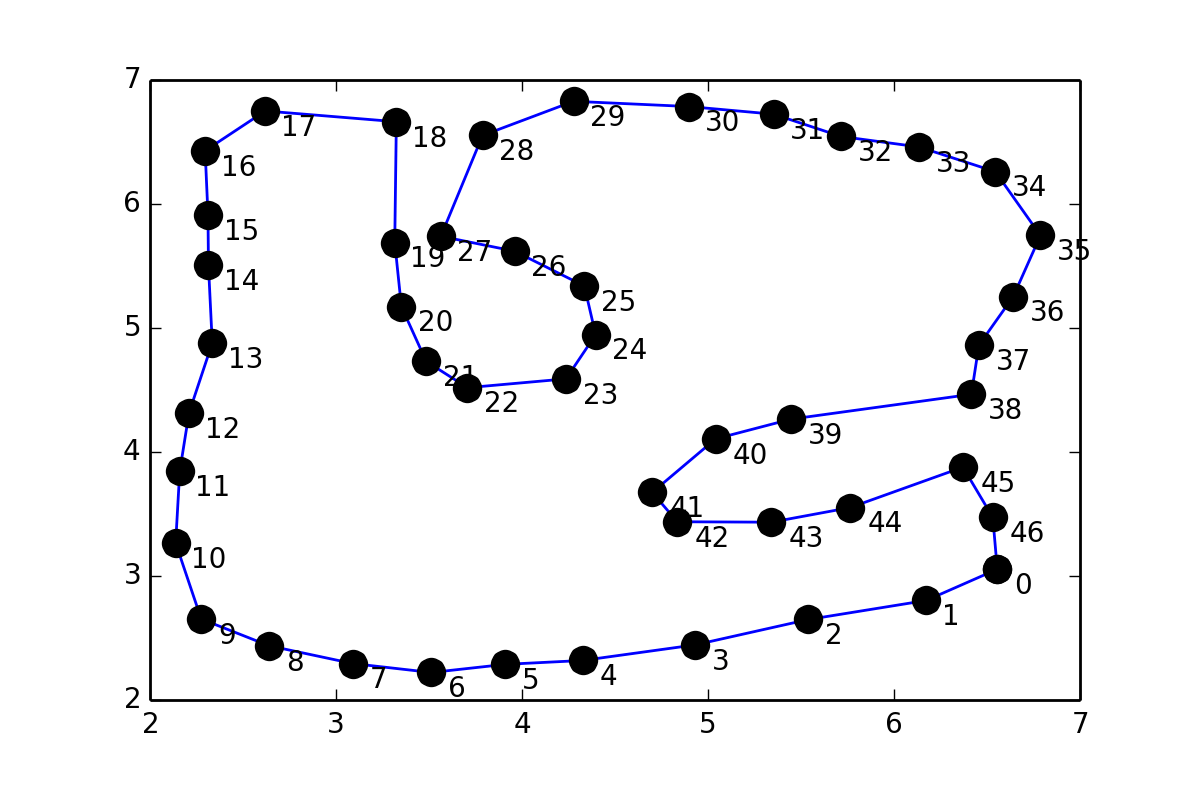
Это немного похоже на 31243002, но вместо того, чтобы помещать точки между парами точек, я хотел бы провести плавную кривую через точки (координаты даны в конце вопроса), поэтому я попробовал что-то похожее на scipy документация по интерполяции:
values = pts
tck = interpolate.splrep(values[:,0], values[:,1], s=1)
xnew = np.arange(2,7,0.01)
ynew = interpolate.splev(xnew, tck, der=0)
но я получаю эту ошибку:
ValueError: Ошибка на входных данных
Есть ли способ найти такую посадку?
Координаты точек:
pts = array([[ 6.55525 , 3.05472 ],
[ 6.17284 , 2.802609],
[ 5.53946 , 2.649209],
[ 4.93053 , 2.444444],
[ 4.32544 , 2.318749],
[ 3.90982 , 2.2875 ],
[ 3.51294 , 2.221875],
[ 3.09107 , 2.29375 ],
[ 2.64013 , 2.4375 ],
[ 2.275444, 2.653124],
[ 2.137945, 3.26562 ],
[ 2.15982 , 3.84375 ],
[ 2.20982 , 4.31562 ],
[ 2.334704, 4.87873 ],
[ 2.314264, 5.5047 ],
[ 2.311709, 5.9135 ],
[ 2.29638 , 6.42961 ],
[ 2.619374, 6.75021 ],
[ 3.32448 , 6.66353 ],
[ 3.31582 , 5.68866 ],
[ 3.35159 , 5.17255 ],
[ 3.48482 , 4.73125 ],
[ 3.70669 , 4.51875 ],
[ 4.23639 , 4.58968 ],
[ 4.39592 , 4.94615 ],
[ 4.33527 , 5.33862 ],
[ 3.95968 , 5.61967 ],
[ 3.56366 , 5.73976 ],
[ 3.78818 , 6.55292 ],
[ 4.27712 , 6.8283 ],
[ 4.89532 , 6.78615 ],
[ 5.35334 , 6.72433 ],
[ 5.71583 , 6.54449 ],
[ 6.13452 , 6.46019 ],
[ 6.54478 , 6.26068 ],
[ 6.7873 , 5.74615 ],
[ 6.64086 , 5.25269 ],
[ 6.45649 , 4.86206 ],
[ 6.41586 , 4.46519 ],
[ 5.44711 , 4.26519 ],
[ 5.04087 , 4.10581 ],
[ 4.70013 , 3.67405 ],
[ 4.83482 , 3.4375 ],
[ 5.34086 , 3.43394 ],
[ 5.76392 , 3.55156 ],
[ 6.37056 , 3.8778 ],
[ 6.53116 , 3.47228 ]])
4 ответа
На самом деле, вы были недалеко от решения вашего вопроса.
С помощью scipy.interpolate.splprepдля параметрической B-сплайновой интерполяции будет самый простой подход. Он также изначально поддерживает замкнутые кривые, если вы предоставляете per=1 параметр,
import numpy as np
from scipy.interpolate import splprep, splev
import matplotlib.pyplot as plt
# define pts from the question
tck, u = splprep(pts.T, u=None, s=0.0, per=1)
u_new = np.linspace(u.min(), u.max(), 1000)
x_new, y_new = splev(u_new, tck, der=0)
plt.plot(pts[:,0], pts[:,1], 'ro')
plt.plot(x_new, y_new, 'b--')
plt.show()
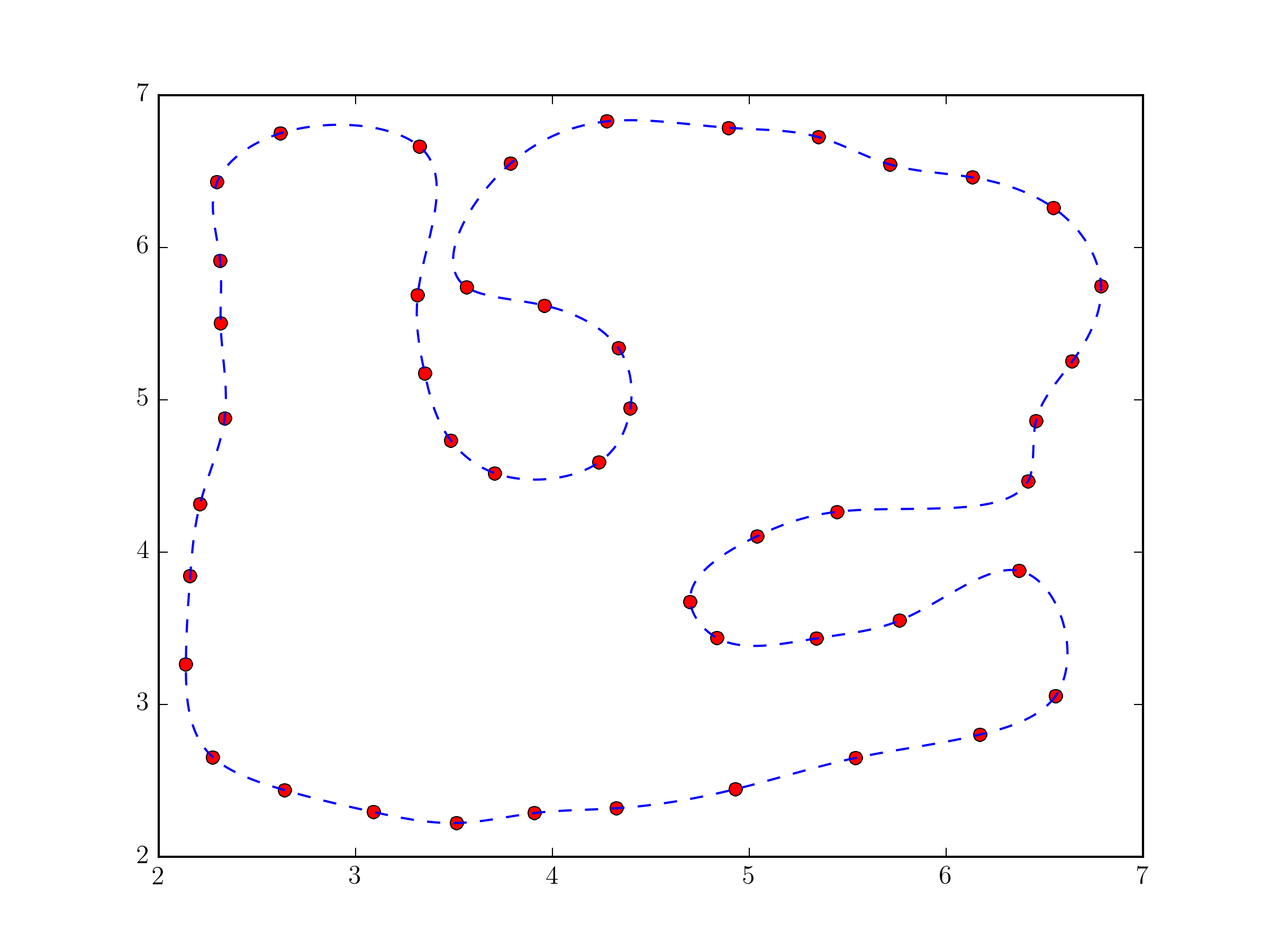
По сути, этот подход не сильно отличается от того, который был в ответе @Joe Kington. Хотя это, вероятно, будет немного более надежным, потому что эквивалент i вектор выбирается по умолчанию исходя из расстояний между точками, а не просто из их индекса (см. splprep документация для u параметр).
Ваша проблема в том, что вы пытаетесь работать с x и y напрямую. Интерполяционная функция, которую вы вызываете, предполагает, что значения x расположены в отсортированном порядке и что каждый x значение будет иметь уникальное значение у.
Вместо этого вам нужно создать параметризованную систему координат (например, индекс ваших вершин) и отдельно интерполировать x и y, используя ее.
Для начала рассмотрим следующее:
import numpy as np
from scipy.interpolate import interp1d # Different interface to the same function
import matplotlib.pyplot as plt
#pts = np.array([...]) # Your points
x, y = pts.T
i = np.arange(len(pts))
# 5x the original number of points
interp_i = np.linspace(0, i.max(), 5 * i.max())
xi = interp1d(i, x, kind='cubic')(interp_i)
yi = interp1d(i, y, kind='cubic')(interp_i)
fig, ax = plt.subplots()
ax.plot(xi, yi)
ax.plot(x, y, 'ko')
plt.show()
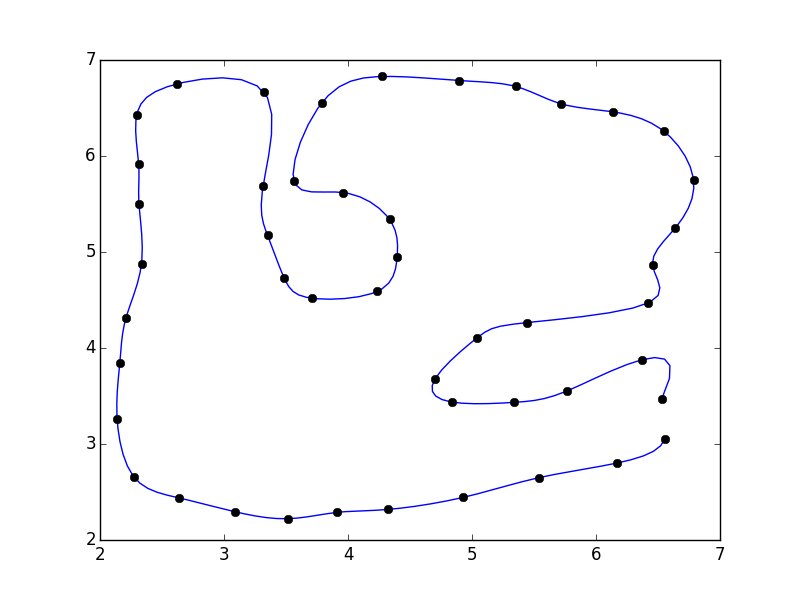
Я не закрывал многоугольник. Если вы хотите, вы можете добавить первую точку в конец массива (например, pts = np.vstack([pts, pts[0]])
Если вы сделаете это, вы заметите, что есть разрыв, где полигон закрывается.
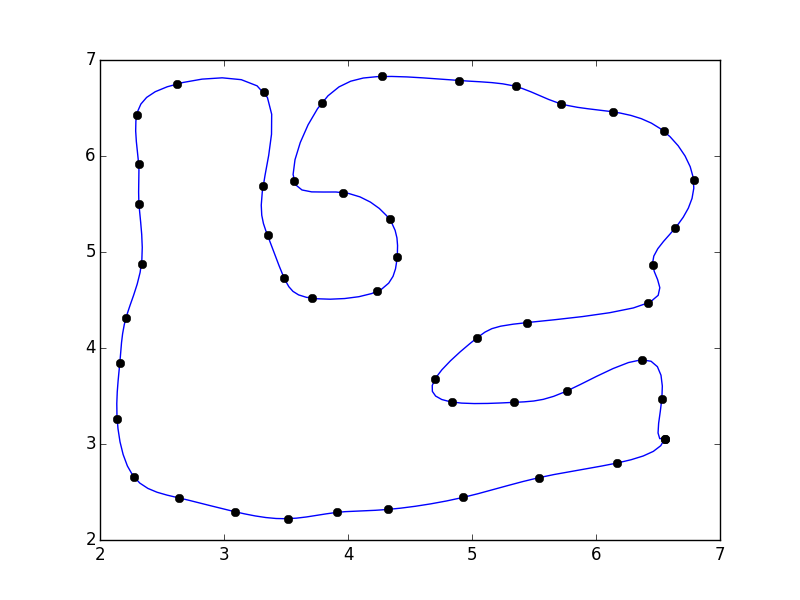
Это потому, что наша параметризация не учитывает закрытие полигона. Быстрое решение состоит в том, чтобы заполнить массив "отраженными" точками:
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
#pts = np.array([...]) # Your points
pad = 3
pts = np.pad(pts, [(pad,pad), (0,0)], mode='wrap')
x, y = pts.T
i = np.arange(0, len(pts))
interp_i = np.linspace(pad, i.max() - pad + 1, 5 * (i.size - 2*pad))
xi = interp1d(i, x, kind='cubic')(interp_i)
yi = interp1d(i, y, kind='cubic')(interp_i)
fig, ax = plt.subplots()
ax.plot(xi, yi)
ax.plot(x, y, 'ko')
plt.show()
В качестве альтернативы вы можете использовать специализированный алгоритм сглаживания кривой, такой как PEAK или алгоритм обрезки углов.
Используя ROOT Framework и интерфейс Pyroot, я смог создать следующее изображение 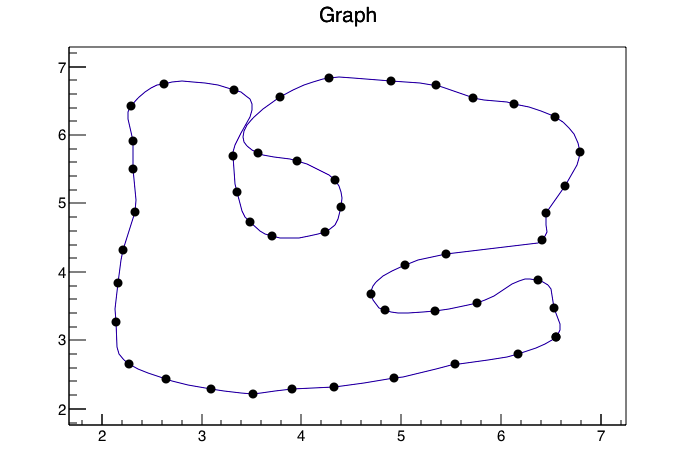
С помощью следующего кода (я конвертировал ваши данные в файл CSV с именем data.csv, так что было бы проще прочитать их в ROOT и дать заголовкам столбцов xp,yp)
from ROOT import TTree, TGraph, TCanvas, TH2F
c1 = TCanvas( 'c1', 'Drawing Example', 200, 10, 700, 500 )
t=TTree('TP','Data Points')
t.ReadFile('./data.csv')
t.SetMarkerStyle(8)
t.Draw("yp:xp","","ACP")
c1.Print('pydraw.png')
Чтобы подогнать гладкую замкнутую кривую через N точек, вы можете использовать отрезки со следующими ограничениями:
- Каждый отрезок должен касаться двух своих конечных точек (2 условия на отрезок)
- Для каждой точки левый и правый отрезок должны иметь одинаковую производную (2 условия на точку == 2 условия на отрезок)
Чтобы иметь достаточно свободы для всех 4 условий на отрезок, уравнение каждого отрезка должно быть y = ax^3 + bx^2 + cx + d. (поэтому производная y' = 3ax^2 + 2bx + c)
Установка условий, как предложено, даст вам N * 4 линейных уравнений для N * 4 неизвестных (a1..aN, b1..bN, c1..cN, d1..dN), разрешимых путем обращения матрицы (numpy).
Если точки находятся на одной и той же вертикальной линии, требуется специальная (но простая) обработка, поскольку производная будет "бесконечной".