Является ли лучший первый поиск оптимальным и полным?
У меня есть некоторые сомнения относительно лучшего первого алгоритма поиска. У меня есть псевдокод: лучший псевдокод поиска в первую очередь
Первое сомнение: это завершено? Я читал, что это не потому, что он может войти в тупик, но я не знаю, когда это может произойти, потому что, если алгоритм выбирает узел, который не имеет больше соседей, он не застревает в нем, потому что этот узел удаляется из открытого списка и на следующей итерации обрабатывается следующий узел открытого списка, и поиск продолжается.
Второе сомнение: это оптимально? Я думал, что если он посещает узлы ближе к цели в процессе поиска, то решение будет самым коротким, но это не так, и я не знаю причину этого и, следовательно, причину, которая делает это алгоритм не оптимальный.
Эвристика, которую я использовал, - это расстояние по прямой между двумя точками.
Спасибо за вашу помощь!!
1 ответ
Конечно, если эвристическая функция недооценивает затраты, лучший первый поиск не является оптимальным. На самом деле, даже если ваша эвристическая функция в точности верна, лучший первый поиск никогда не будет гарантированно оптимальным. Вот контрпример. Рассмотрим следующий график:
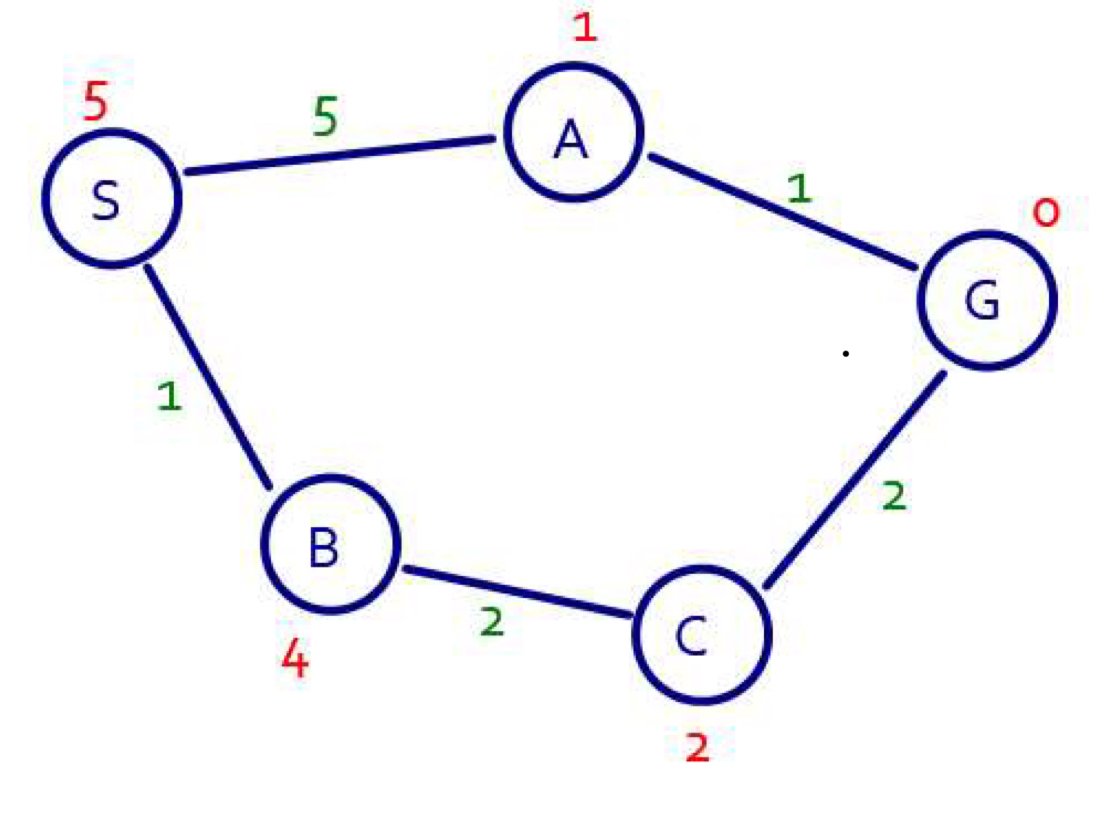Зеленые числа - это фактические затраты, а красные - точная эвристическая функция. Давайте попробуем найти путь от узла S к узлу G. Лучший первый поиск даст вам S->A->G, следуя эвристической функции. Однако, если вы посмотрите на график ближе, вы увидите, что путь S->B->C->G имеет меньшую стоимость, чем 5, а не 6. Таким образом, это пример наилучшего первого поиска, выполняющего неоптимально при совершенной эвристике функция.
В общем случае лучший алгоритм первого поиска завершен, так как в худшем случае он будет искать все пространство (худший вариант). Теперь она также должна быть оптимальной - учитывая, что эвристическая функция допустима - это означает, что она не переоценивает стоимость пути от любого из узлов до цели. (Он также должен быть последовательным - это означает, что он придерживается неравенства треугольника, если это не так, алгоритм не будет завершен - как он может войти в цикл)
Проверяя ваш алгоритм, я не вижу, как вычисляется эвристическая функция. Также я не вижу там рассчитывается стоимость пути, чтобы добраться до конкретного узла. Таким образом, ему необходимо рассчитать фактическую стоимость пути для достижения конкретного узла, а затем добавить эвристическую оценку стоимости пути от узла к цели.
Формула f(n)=g(n)+h(n) где g (n) - это стоимость пути для достижения узла, а h (n) - эвристика, оценивающая стоимость самого дешевого пути от n до цели.
Проверьте реализацию алгоритма A *, который является примером наилучшего первого поиска при планировании пути.
TLDR В первом наилучшем поиске необходимо рассчитать стоимость узла как сумму стоимости пути до этого узла и эвристической функции, которая оценивает стоимость пути от этого узла до цели. Если эвристическая функция будет допустимой и согласованной, алгоритм будет оптимальным и полным.