Подходящая модель SIR на основе наименьших квадратов

Question

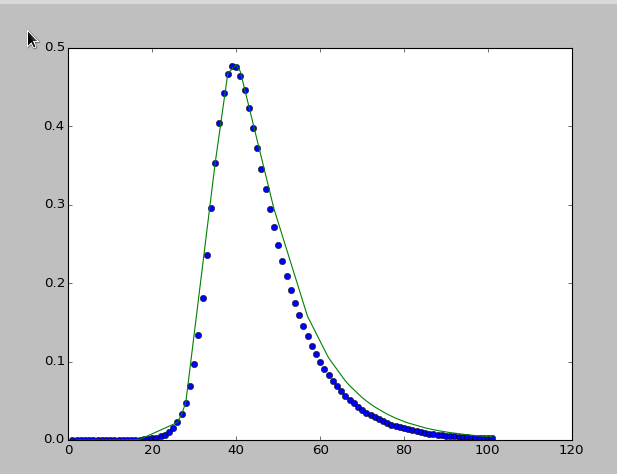
Я хотел бы оптимизировать примерку модели SIR. Если я соответствую модели SIR только с 60 точками данных, я получаю "хороший" результат. "Хороший" означает, что подобранная модельная кривая близка к точкам данных до t=40. У меня вопрос, как я могу получить лучшую подгонку, возможно, на основе всех точек данных?

ydata = ['1e-06', '1.49920166169172e-06', '2.24595472686361e-06', '3.36377954575331e-06', '5.03793663882291e-06', '7.54533628058909e-06', '1.13006564683911e-05', '1.69249500601052e-05', '2.53483161761933e-05', '3.79636391699325e-05', '5.68567547875179e-05', '8.51509649182741e-05', '0.000127522555808945', '0.000189928392105942', '0.000283447055673738', '0.000423064043409294', '0.000631295993246634', '0.000941024110897193', '0.00140281896645859', '0.00209085569326554', '0.00311449589149717', '0.00463557784224762', '0.00689146863803467', '0.010227347567051', '0.0151380084180746', '0.0223233100045688', '0.0327384810150231', '0.0476330618585758', '0.0685260046667727', '0.0970432959143974', '0.134525888779423', '0.181363340075877', '0.236189247803334', '0.295374180276257', '0.353377036130714', '0.404138746080267', '0.442876028839178', '0.467273954573897', '0.477529937494976', '0.475582401936257', '0.464137179474659', '0.445930281787152', '0.423331710456602', '0.39821360956389', '0.371967226561944', '0.345577884704341', '0.319716449520481', '0.294819942458255', '0.271156813453547', '0.24887641905719', '0.228045466022105', '0.208674420183194', '0.190736203926912', '0.174179448652951', '0.158937806544529', '0.144936441326754', '0.132096533873646', '0.120338367115739', '0.10958340819268', '0.099755679236243', '0.0907826241267504', '0.0825956203546979', '0.0751302384111894', '0.0683263295744258', '0.0621279977639921', '0.0564834809370572', '0.0513449852139111', '0.0466684871328814', '0.042413516167789', '0.0385429293775096', '0.035022685071934', '0.0318216204865132', '0.0289112368382048', '0.0262654939162707', '0.0238606155312519', '0.021674906523588', '0.0196885815912485', '0.0178836058829335', '0.0162435470852779', '0.0147534385851646', '0.0133996531928511', '0.0121697868544064', '0.0110525517526551', '0.0100376781867076', '0.00911582462544914', '0.00827849534575178', '0.00751796508841916', '0.00682721019158058', '0.00619984569061827', '0.00563006790443123', '0.00511260205894446', '0.00464265452957236', '0.00421586931435123', '0.00382828837833139', '0.00347631553734708', '0.00315668357532714', '0.00286642431380459', '0.00260284137520731', '0.00236348540287827', '0.00214613152062159', '0.00194875883295343']
ydata = [float(d) for d in ydata]
xdata = ['1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18', '19', '20', '21', '22', '23', '24', '25', '26', '27', '28', '29', '30', '31', '32', '33', '34', '35', '36', '37', '38', '39', '40', '41', '42', '43', '44', '45', '46', '47', '48', '49', '50', '51', '52', '53', '54', '55', '56', '57', '58', '59', '60', '61', '62', '63', '64', '65', '66', '67', '68', '69', '70', '71', '72', '73', '74', '75', '76', '77', '78', '79', '80', '81', '82', '83', '84', '85', '86', '87', '88', '89', '90', '91', '92', '93', '94', '95', '96', '97', '98', '99', '100', '101']
xdata = [float(t) for t in xdata]

from scipy.optimize import minimize
from scipy import integrate
import numpy as np
import pylab as pl

def fitFunc(sir_values, time, beta, gamma, k):
    s = sir_values[0]
    i = sir_values[1]
    r = sir_values[2]

    res = np.zeros((3))
    res[0] = - beta * s * i
    res[1] = beta * s * i - gamma * i
    res[2] = gamma * i
    return res

def lsq(model, xdata, ydata, n):
    """least squares"""
    time_total = xdata
    # original record data
    data_record = ydata
    # normalize train data
    k = 1.0/sum(data_record)
    # init t = 0 values + normalized
    I0 = data_record[0]*k
    S0 = 1 - I0
    R0 = 0 
    N0 = [S0,I0,R0]
    # Set initial parameter values
    param_init = [0.75, 0.75]
    param_init.append(k)
    # fitting
    param = minimize(sse(model, N0, time_total, k, data_record, n), param_init, method="nelder-mead").x
    # get the fitted model
    Nt = integrate.odeint(model, N0, time_total, args=tuple(param))
    # scale out
    Nt = np.divide(Nt, k)
    # Get the second column of data corresponding to I
    return Nt[:,1]

def sse(model, N0, time_total, k, data_record, n):
    """sum of square errors"""
    def result(x):
        Nt = integrate.odeint(model, N0, time_total[:n], args=tuple(x))
        INt = [row[1] for row in Nt]
        INt = np.divide(INt, k)
        difference = data_record[:n] - INt
        # square the difference
        diff = np.dot(difference, difference)
        return diff
    return result

result = lsq(fitFunc, xdata, ydata, 60)

# Plot data and fit
pl.clf()
pl.plot(xdata, ydata, "o")
pl.plot(xdata, result)
pl.show()

Я ожидаю что-то вроде этого:

Answer 1

Я конвертирую свой комментарий в полноценный ответ.

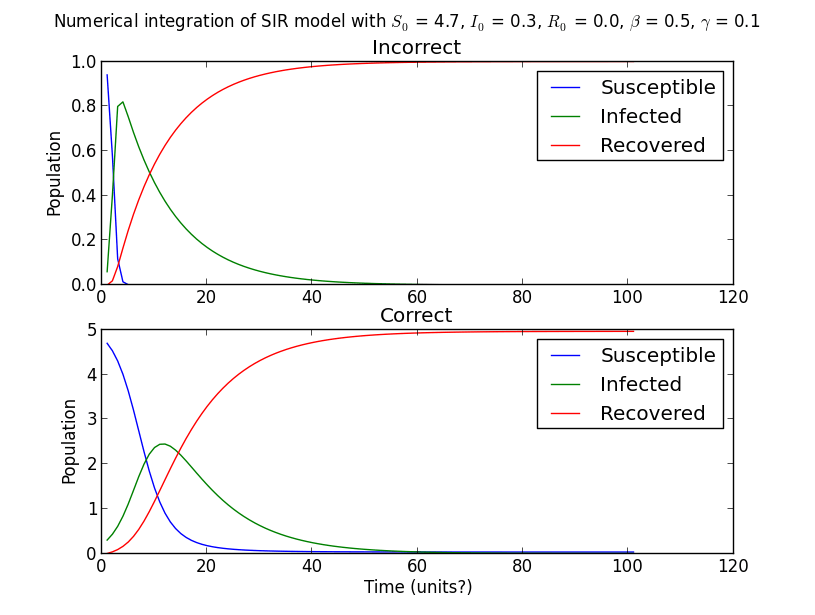
Проблема возникает из-за неправильной настройки модели. Чтобы упростить дифференциальные уравнения, я буду ссылаться на dS(t)/dt а также dI(t)/dt как S а также I соответственно.

# incorrect
S = -S * I * beta
I = S * I * beta - I * gamma

# correct
S = -S * I * beta / N
I = S * I * beta / N - I * gamma

При неправильной настройке дифференциальных уравнений скорость изменения, т. Е. Переход от y(t) к y(t+dt), является неправильной. Таким образом, вы не только получаете неправильно интегрированный I(t), но и дополнительно делите его на N (или k, как вы его назвали), делая его еще более неправильным.

Мы знаем, что связанная система этих конкретных уравнений требует, чтобы S(t) + I(t) + R(t) = N, где N - постоянная населенности. Исходя из того, как вы объявляете начальные условия, мы заключаем, что N равно 1. Обратите внимание, что это также согласуется с max(ydata), что меньше 1.

# IO + SO + R0 is always 1 regardless of "value"
I0 = value
S0 = 1 - I0
R0 = 0

Кроме того, как вы справляетесь k действительно сомнительно Кажется, ваши данные уже нормализованы, но вы умножаете их на коэффициент 0,1. Как вы видете, k = 1./sum(ydata), не имеет ничего общего с константой населения. При выполнении I0 = ydata[0] * k и деление I (t) на kвы эффективно уменьшаете свои данные только для того, чтобы потом их масштабировать. Это в значительной степени ограничивает I (t) в диапазоне 0-1, независимо от того, какова константа населения.

Вы можете проверить, что ваша модель неверна, просто установив все начальные условия и неизвестные параметры и посмотрев, что получается odeint(), Вы заметите, что S(0), I(0) и R(0) могут не соответствовать значениям, которые вы им даете, что является признаком неправильных действий k, Но чтобы обнаружить ошибочную динамику эволюции, вы должны просто пересмотреть свою модель.

Хакерское решение было бы установить k = 1.0, Все работает, потому что умножения и деления не имеют никакого эффекта, даже если вы все еще технически делаете неправильные вычисления. Однако, если ваша константа населения когда-либо будет отличаться от 1, все сломается. Итак, для тщательности,

• установить вручную k к константе населения, которую вы должны знать в любом случае, если только вы не пытаетесь соответствовать S0, I0 и / или R0.

• Напишите правильную скорость изменения в модели для S а также I,

• Избавиться от любого np.divide(array, k) расчеты у вас есть, и

• Удалить k от fitFunc() аргументы и не добавляйте его к param_init список. Хотя это последнее действие не является обязательным и не влияет на результат, оно все равно технически правильно. Это потому что мимоходом kоптимизатор пытается найти для него оптимальное значение, даже если вы нигде не используете его, чтобы повлиять на ваши вычисления.

Решение той же проблемы с кривой_fit()

Если вы хотите выполнить подгонку по методу наименьших квадратов, вы можете использовать функцию curve_fit(), которая внутренне вызывает метод наименьших квадратов. Вам все еще нужно будет создать функцию-обертку для фитинга, которая должна численно интегрировать систему для различных значений бета и гаммы, но вам не нужно будет делать какие-либо вычисления SSE вручную.

curve_fit() также вернет ковариационную матрицу, которую вы можете использовать для оценки доверительных интервалов для ваших подогнанных переменных. Дальнейшее связанное обсуждение по вычислению доверительных интервалов из ковариационной матрицы можно найти здесь.

import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate, optimize

ydata = ['1e-06', '1.49920166169172e-06', '2.24595472686361e-06', '3.36377954575331e-06', '5.03793663882291e-06', '7.54533628058909e-06', '1.13006564683911e-05', '1.69249500601052e-05', '2.53483161761933e-05', '3.79636391699325e-05', '5.68567547875179e-05', '8.51509649182741e-05', '0.000127522555808945', '0.000189928392105942', '0.000283447055673738', '0.000423064043409294', '0.000631295993246634', '0.000941024110897193', '0.00140281896645859', '0.00209085569326554', '0.00311449589149717', '0.00463557784224762', '0.00689146863803467', '0.010227347567051', '0.0151380084180746', '0.0223233100045688', '0.0327384810150231', '0.0476330618585758', '0.0685260046667727', '0.0970432959143974', '0.134525888779423', '0.181363340075877', '0.236189247803334', '0.295374180276257', '0.353377036130714', '0.404138746080267', '0.442876028839178', '0.467273954573897', '0.477529937494976', '0.475582401936257', '0.464137179474659', '0.445930281787152', '0.423331710456602', '0.39821360956389', '0.371967226561944', '0.345577884704341', '0.319716449520481', '0.294819942458255', '0.271156813453547', '0.24887641905719', '0.228045466022105', '0.208674420183194', '0.190736203926912', '0.174179448652951', '0.158937806544529', '0.144936441326754', '0.132096533873646', '0.120338367115739', '0.10958340819268', '0.099755679236243', '0.0907826241267504', '0.0825956203546979', '0.0751302384111894', '0.0683263295744258', '0.0621279977639921', '0.0564834809370572', '0.0513449852139111', '0.0466684871328814', '0.042413516167789', '0.0385429293775096', '0.035022685071934', '0.0318216204865132', '0.0289112368382048', '0.0262654939162707', '0.0238606155312519', '0.021674906523588', '0.0196885815912485', '0.0178836058829335', '0.0162435470852779', '0.0147534385851646', '0.0133996531928511', '0.0121697868544064', '0.0110525517526551', '0.0100376781867076', '0.00911582462544914', '0.00827849534575178', '0.00751796508841916', '0.00682721019158058', '0.00619984569061827', '0.00563006790443123', '0.00511260205894446', '0.00464265452957236', '0.00421586931435123', '0.00382828837833139', '0.00347631553734708', '0.00315668357532714', '0.00286642431380459', '0.00260284137520731', '0.00236348540287827', '0.00214613152062159', '0.00194875883295343']
xdata = ['1', '2', '3', '4', '5', '6', '7', '8', '9', '10', '11', '12', '13', '14', '15', '16', '17', '18', '19', '20', '21', '22', '23', '24', '25', '26', '27', '28', '29', '30', '31', '32', '33', '34', '35', '36', '37', '38', '39', '40', '41', '42', '43', '44', '45', '46', '47', '48', '49', '50', '51', '52', '53', '54', '55', '56', '57', '58', '59', '60', '61', '62', '63', '64', '65', '66', '67', '68', '69', '70', '71', '72', '73', '74', '75', '76', '77', '78', '79', '80', '81', '82', '83', '84', '85', '86', '87', '88', '89', '90', '91', '92', '93', '94', '95', '96', '97', '98', '99', '100', '101']

ydata = np.array(ydata, dtype=float)
xdata = np.array(xdata, dtype=float)

def sir_model(y, x, beta, gamma):
    S = -beta * y[0] * y[1] / N
    R = gamma * y[1]
    I = -(S + R)
    return S, I, R

def fit_odeint(x, beta, gamma):
    return integrate.odeint(sir_model, (S0, I0, R0), x, args=(beta, gamma))[:,1]

N = 1.0
I0 = ydata[0]
S0 = N - I0
R0 = 0.0

popt, pcov = optimize.curve_fit(fit_odeint, xdata, ydata)
fitted = fit_odeint(xdata, *popt)

plt.plot(xdata, ydata, 'o')
plt.plot(xdata, fitted)
plt.show()

Вы можете заметить некоторые предупреждения во время выполнения, но они в основном из-за начального поиска решателя минимизации (Levenburg-Marquardt), который пытается некоторые значения для beta а также gamma которые вызывают числовые переполнения во время интеграции. Тем не менее, он должен скоро прийти к более разумным значениям. Если вы попробуете разные решатели для minimize()Вы заметите аналогичные предупреждения.