Исправление ошибки дрейфа SLAM с помощью измерений GPS

Question

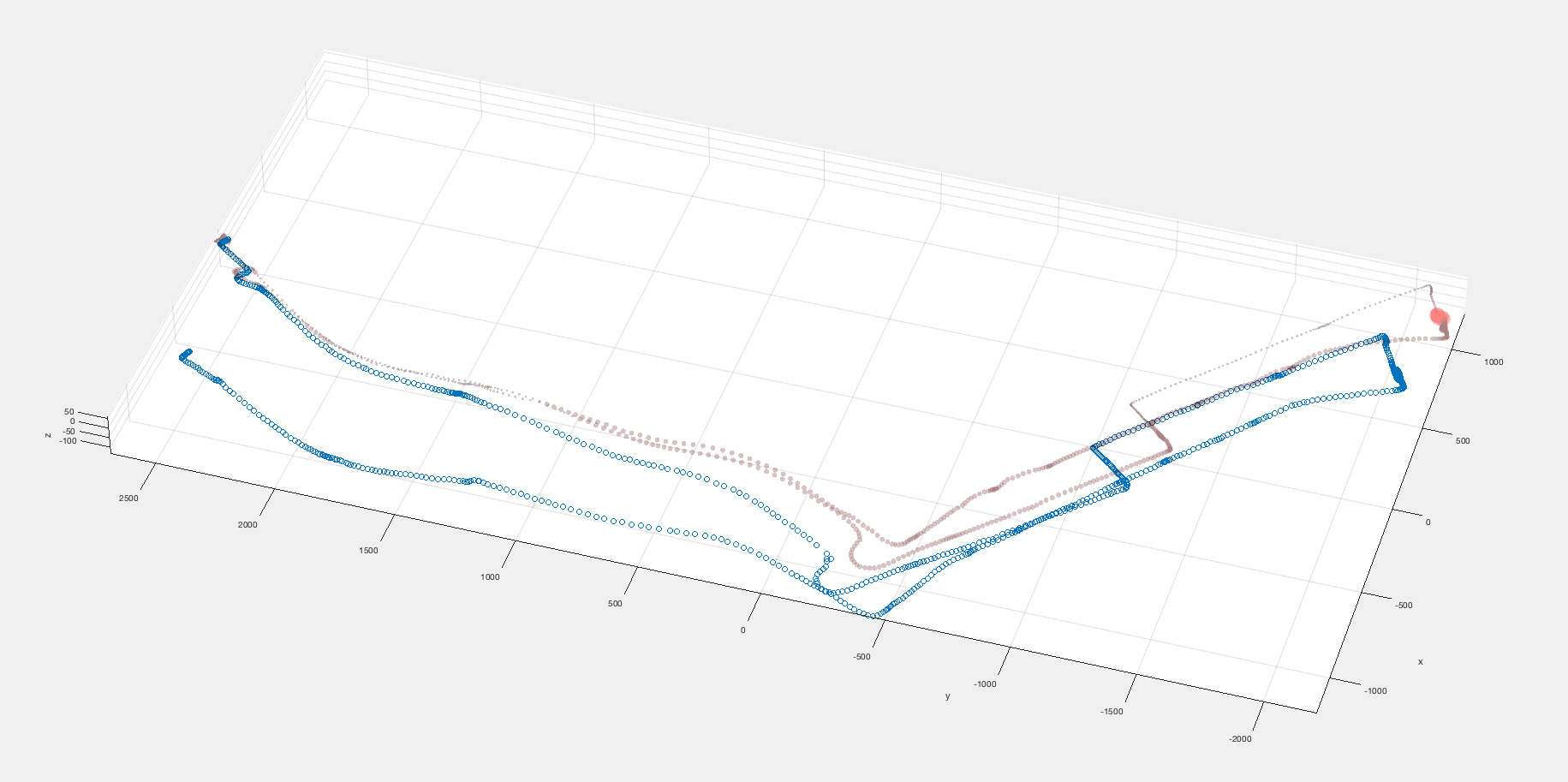
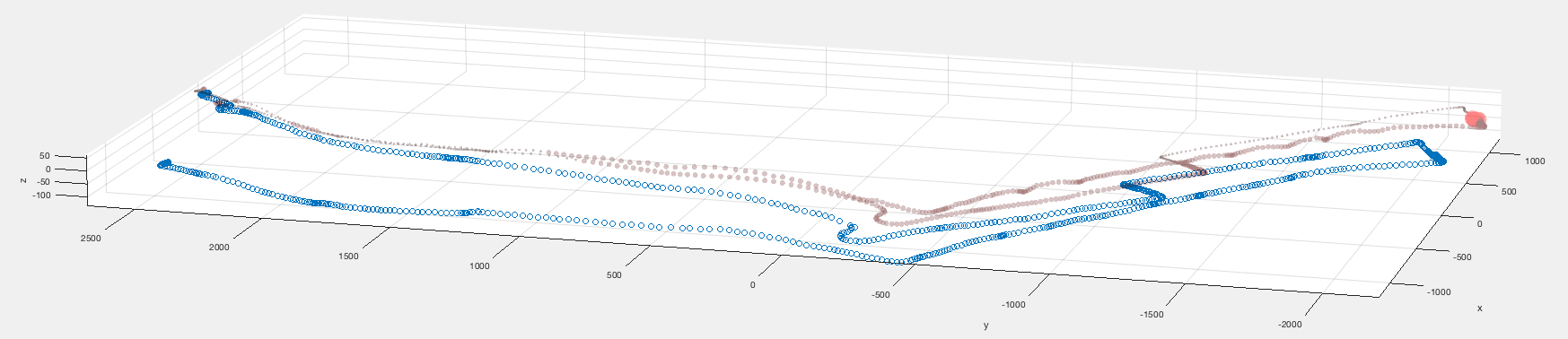
Я пытаюсь выяснить, как исправить ошибки дрейфа, вызванные методом SLAM с использованием измерений GPS, у меня есть два набора точек в евклидовом трехмерном пространстве, взятые в фиксированные моменты времени:

Красный набор данных введен GPS и не содержит ошибок дрейфа, в то время как синий набор данных основан на алгоритме SLAM, он дрейфует со временем.

Идея состоит в том, что SLAM точен на коротких расстояниях, но в конечном итоге дрейфует, в то время как GPS точен на больших расстояниях и неточен на коротких. Поэтому я хотел бы выяснить, как объединить данные SLAM с GPS таким образом, чтобы обеспечить максимальную точность обоих измерений. Хотя бы как подойти к этой проблеме?

Answer 1

Поскольку ваш GPS выглядит как локально смещенный, я предполагаю, что он недорогой и не использует никаких методов коррекции, например, что он не является дифференциальным. Как вы, наверное, знаете, ошибки GPS не являются гауссовыми. Ребята из этой статьи показывают, что хороший способ смоделировать шум GPS v+eps где v является локально постоянным вектором "смещения" (он обычно постоянен в течение нескольких метров, а затем изменяется более или менее плавно или резко) и eps гауссовский шум

Учитывая эту информацию, одним из вариантов будет использование слияния на основе Калмана, например, вы добавляете шум GPS и смещение к вектору состояний, и соответственно определяете свои уравнения перехода и продолжаете, как если бы вы работали с обычным EKF. Обратите внимание, что если мы игнорируем шаг предсказания Калмана, это примерно эквивалентно минимизации функции ошибки вида

   measurement_constraints + some_weight * GPS_constraints 

и это дает вам более прямой, второй вариант. Например, если ваш SLAM визуальный, вы можете просто использовать сумму квадратичных ошибок перепроецирования (то есть ошибки настройки пучка) в качестве ограничений измерения и определить свои ограничения GPS как ||x- x_{gps}|| где x являются 2d или же 3d GPS-координаты (вы можете игнорировать высоту с помощью недорогого GPS).

Если ваш SLAM визуален и основан на характерных точках (вы на самом деле не сказали, какой тип SLAM вы использовали, поэтому я предполагаю, что он является наиболее распространенным типом), то объединение с любым из перечисленных выше методов может привести к "внутренней потере". Вы делаете внезапную насильственную коррекцию и увеличиваете количество ошибок перепроецирования. Это означает, что вы теряете вкладыши в слежении за SLAM. Таким образом, вы должны повторно триангулировать точки и так далее. Кроме того, обратите внимание, что хотя в статье, на которую я ссылался выше, представлена ​​модель ошибок GPS, это не очень точная модель, и если предположить, что распределение ошибок GPS является унимодальным (необходимым для EKF), мне кажется, что это немного авантюрно,

Поэтому я думаю, что хорошим вариантом является использование барьерной оптимизации. По сути, идея такова: поскольку вы на самом деле не знаете, как моделировать ошибки GPS, предположите, что у вас больше доверия в SLAM локально, и минимизируйте функцию S(x) это отражает качество вашей реконструкции SLAM. Заметка x_opt минимизатор S, Затем слиться с данными GPS, если они не портятся S(x_opt) больше заданного порога. Математически вы бы хотели минимизировать

some_coef/(thresh - S(X))  + ||x-x_{gps}||

и вы бы инициализировали минимизацию с x_opt, Хороший выбор для S является ошибкой настройки связки, поскольку, не уменьшая ее, вы предотвращаете потерю inlier. Есть и другие варианты S в литературе, но они, как правило, предназначены для сокращения времени вычислений и добавления немного с точки зрения точности.

Это, в отличие от EKF, не имеет хорошей вероятностной интерпретации, но дает очень хорошие результаты на практике (я использовал его для объединения с другими вещами, кроме GPS, и он работает хорошо). Например, вы можете увидеть этот превосходный документ, в котором объясняется, как его тщательно реализовать, как установить порог и т. Д.

Надеюсь это поможет. Пожалуйста, не стесняйтесь сообщить мне, если вы найдете неточности / ошибки в моем ответе.