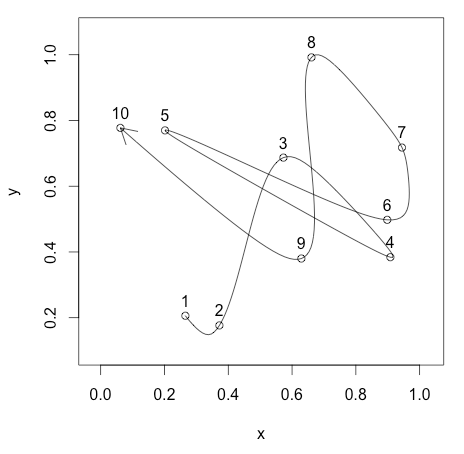
Рассчитать двухмерную сплайн-кривую в R

Question

Я пытаюсь вычислить сплайновую кривую Безье, которая проходит через последовательность координат xy. Пример был бы похож на следующий вывод из cscvn функция в Matlab ( пример ссылки):

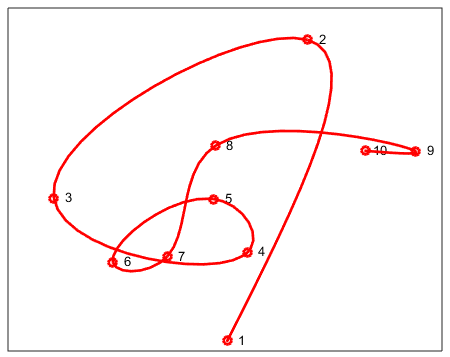
Я верю (больше не поддерживается) grid пакет, используемый для этого (grid.xspline функция?), но я не смог установить заархивированную версию пакета, и я не нахожу никаких примеров в точности так, как мне хотелось бы.

bezier Пакет также выглядит многообещающе, но он очень медленный, и я также не могу сделать это совершенно правильно:

library(bezier)

set.seed(1)
n <- 10
x <- runif(n)
y <- runif(n)
p <- cbind(x,y)
xlim <- c(min(x) - 0.1*diff(range(x)), c(max(x) + 0.1*diff(range(x))))
ylim <- c(min(y) - 0.1*diff(range(y)), c(max(y) + 0.1*diff(range(y))))
plot(p, xlim=xlim, ylim=ylim)
text(p, labels=seq(n), pos=3)

bp <- pointsOnBezier(cbind(x,y), n=100)
lines(bp$points)
arrows(bp$points[nrow(bp$points)-1,1], bp$points[nrow(bp$points)-1,2],
  bp$points[nrow(bp$points),1], bp$points[nrow(bp$points),2]
)

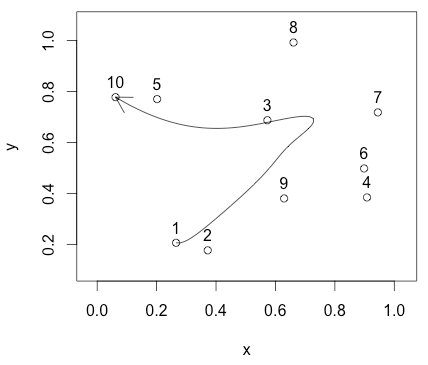
Как видите, он не проходит через какие-либо точки, кроме конечных значений.

Я был бы очень признателен за некоторые указания здесь!

Answer 1

Это может быть не самый лучший подход, немного grid конечно не неактивен. Он включен в качестве пакета по умолчанию с установкой R. Это базовый графический движок для построения таких библиотек, как lattice и ggplot. Вам не нужно устанавливать его, вы можете просто загрузить его. Вот как я мог бы перевести ваш код для использования grid.xpline

set.seed(1)
n <- 10
x <- runif(n)
y <- runif(n)
xlim <- c(min(x) - 0.1*diff(range(x)), c(max(x) + 0.1*diff(range(x))))
ylim <- c(min(y) - 0.1*diff(range(y)), c(max(y) + 0.1*diff(range(y))))

library(grid)
grid.newpage()
pushViewport(viewport(xscale=xlim, yscale=ylim))
grid.points(x, y, pch=16, size=unit(2, "mm"), 
    default.units="native")
grid.text(seq(n), x,y, just=c("center","bottom"), 
    default.units="native")
grid.xspline(x, y, shape=c(0,rep(-1, 10-2),0), open=TRUE, 
    default.units="native")
popViewport()

что приводит к

обратите внимание, что сетка довольно низкоуровневая, поэтому работать с ней непросто, но она позволяет намного лучше контролировать, что и где вы планируете.

И если вы хотите извлечь точки вдоль кривой, а не нарисовать ее, посмотрите на ?xsplinePoints страница справки.

Answer 2

Там нет необходимости использовать grid действительно. Вы можете получить доступ xspline от graphics пакет.

Исходя из вашего кода и shape от @mrflick:

set.seed(1)
n <- 10
x <- runif(n)
y <- runif(n)
p <- cbind(x,y)
xlim <- c(min(x) - 0.1*diff(range(x)), c(max(x) + 0.1*diff(range(x))))
ylim <- c(min(y) - 0.1*diff(range(y)), c(max(y) + 0.1*diff(range(y))))
plot(p, xlim=xlim, ylim=ylim)
text(p, labels=seq(n), pos=3)

Вам просто нужна одна дополнительная строка:

xspline(x, y, shape = c(0,rep(-1, 10-2),0), border="red")

Answer 3

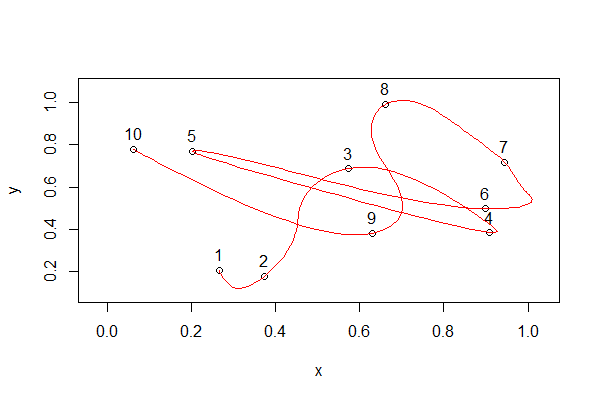
Спасибо всем, кто помог с этим. Я суммирую извлеченные уроки плюс несколько других аспектов.

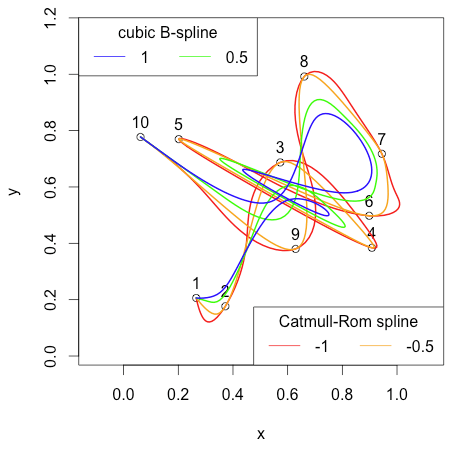
Сплайн Catmull-Rom против кубического B-сплайна

Отрицательные значения формы в xspline Функция возвращает сплайн типа Catmull-Rom, сплайн проходит через точки xy. Положительные значения возвращают кубический сплайн типа B. Нулевые значения возвращают острый угол. Если задано одно значение формы, оно используется для всех точек. Форма конечных точек всегда обрабатывается как острый угол (форма =0), а другие значения не влияют на результирующий сплайн в конечных точках:

# Catmull-Rom spline vs. cubic B-spline
plot(p, xlim=extendrange(x, f=0.2), ylim=extendrange(y, f=0.2))
text(p, labels=seq(n), pos=3)
# Catmull-Rom spline (-1)
xspline(p, shape = -1, border="red", lwd=2) 
# Catmull-Rom spline (-0.5)
xspline(p, shape = -0.5, border="orange", lwd=2) 
# cubic B-spline (0.5)
xspline(p, shape = 0.5, border="green", lwd=2) 
# cubic B-spline (1)
xspline(p, shape = 1, border="blue", lwd=2)
legend("bottomright", ncol=2, legend=c(-1,-0.5), title="Catmull-Rom spline", col=c("red", "orange"), lty=1)
legend("topleft", ncol=2, legend=c(1, 0.5), title="cubic B-spline", col=c("blue", "green"), lty=1)

Извлечение результатов из xspline для внешнего построения

Это потребовало некоторого поиска, но хитрость заключается в том, чтобы применить аргумент draw=FALSE в xspline,

# Extract xy values
plot(p, xlim=extendrange(x, f=0.1), ylim=extendrange(y, f=0.1))
text(p, labels=seq(n), pos=3)
spl <- xspline(x, y, shape = -0.5, draw=FALSE) 
lines(spl)
arrows(x0=(spl$x[length(spl$x)-0.01*length(spl$x)]), y0=(spl$y[length(spl$y)-0.01*length(spl$y)]),
       x1=(spl$x[length(spl$x)]), y1=(spl$y[length(spl$y)])
)