Количество премьер-импликантов и EPI
Мой ТА решает эту проблему, Количество Первичного Импликанта (ИП) для
f(a,b,c,d)= Sigma m(0,2,4,5,8,10,11,13,15)
равно 7, а число основных PI (EPI) равно 1. как это будет рассчитываться? Я думаю, что это неправильно. любая идея?
Мое решение:
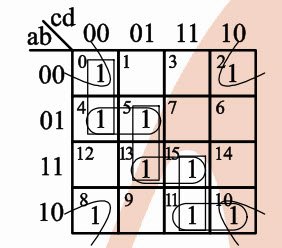
1 ответ
Чтобы предоставить вам больше возможностей для обучения, я проведу процесс графического определения PI и EPI для другой функции, аналогичной вашей. Вы можете использовать точно такой же метод, чтобы затем решить числа для функции, которую вы дали в своем вопросе. Обратите внимание, что существует несколько способов определения PI и EPI, но мне нравится метод Kmap, поскольку он хорошо иллюстрирует концепцию. [ПРИМЕЧАНИЕ: после того, как ОП добавил его решения, я исправил свой ответ, включив в него оригинальную функцию]
Пример:
Допустим, у нас есть эта функция:
g(a,b,c,d) = Sigma m(0,4,7,9,10,11,12,13,15)
И мы хотим определить количество основных импликантов (ПИ) и основных основных импликантов ( http://en.wikipedia.org/wiki/Implicant).
Первым шагом является генерация Kmap ( http://en.wikipedia.org/wiki/Karnaugh_map) для данной функции (так как она задана как сумма минимальных членов, заполните место в Kmap единицами, которые образуют двоичное представление заданного списка терминов):
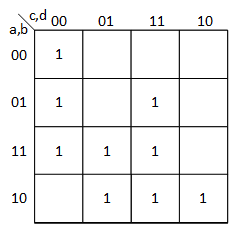
Теперь мы должны найти самые большие покрытия для всех условий Kmap. Число этих самых больших покрытий - это число PI, и каждое наибольшее покрытие является основным импликантом (т. Е. Импликантом или частичной функцией, которая не может быть дополнительно упрощена с помощью любого другого импликанта для формирования более общего импликанта или большего покрытия). Такое покрытие выглядит так:
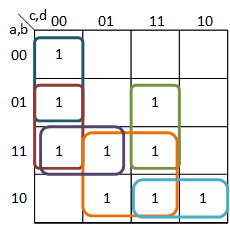
Теперь, когда у нас есть покрытие, мы можем сосчитать эти самые большие покрытия. Есть 6, поэтому есть 6 PI, и эти покрытия представляют их. Теперь, чтобы узнать количество EPI, нам нужно посмотреть, сколько терминов в нашем Kmap покрыто одним-единственным покрытием. Если рассматривать термины, это 0 (только синий), 7 (только зеленый), 9 (только оранжевый) и 10 (только голубой). Таким образом, существует 4 EPI.
Теперь попробуйте этот метод для вашей проблемы и посмотрите, какие цифры вы получите!
[Обновление: вот информация о вашем решении]
И вам Kmap и покрытие мне кажется хорошим:

Как видно из вашего покрытия, всего существует 7 покрытий самого большого размера; 6 по диагонали и 1 большой, охватывающий четыре угла. Таким образом, как описано выше, существует 7 ИП. Чтобы получить EPI, нам нужно увидеть, сколько из этих PIs однозначно охватывают один из терминов, то есть найти термины, охватываемые одним и только одним из наших PI, и это EPI. Глядя на Kmap, только углы с терминами 8 и 2 покрыты только одним PI (т. Е. Покрывают 4 угла). Хотя есть два термина, они разделяют сохранение покрытия и помнят, что покрытия являются косвенными. Таким образом, поскольку существует только одно покрытие, включая термины, охватываемые одним и только одним покрытием, существует только 1 EPI. (Таким образом, ваш TA был правильным; 7 PI и 1 EPI).