Зачем преобразовывать нормали с помощью транспонирования инверсии матрицы вида модели?
Я работаю над некоторыми шейдерами, и мне нужно преобразовать нормали.
В нескольких уроках я читал, как вы преобразуете нормали, умножая их на транспонирование инверсии матрицы вида модели. Но я не могу найти объяснение, почему это так, и какова логика этого?
5 ответов
Взгляните на этот урок:
https://paroj.github.io/gltut/Illumination/Tut09%20Normal%20Transformation.html
Вы можете себе представить, что когда поверхность сферы растягивается (таким образом, сфера масштабируется вдоль одной оси или чего-то подобного), все нормали этой поверхности будут "изгибаться" друг к другу. Оказывается, вам нужно инвертировать шкалу, примененную к нормали, чтобы добиться этого. Это то же самое, что и преобразование с использованием матрицы обратной транспозиции. Ссылка выше показывает, как из этого извлечь обратную матрицу транспонирования.
Также обратите внимание, что если шкала равномерна, вы можете просто передать исходную матрицу как нормальную матрицу. Представьте, что одна и та же сфера масштабируется равномерно по всем осям, поверхность не будет растягиваться или изгибаться, равно как и нормали.
Это вытекает из определения нормального.
Предположим, у вас есть нормальный, Nи вектор, V, касательный вектор в той же позиции на объекте, что и нормаль. Тогда по определению N·V = 0,
Касательные векторы идут в том же направлении, что и поверхность объекта. Таким образом, если ваша поверхность плоская, то касательная - это разница между двумя опознаваемыми точками на объекте. Так что если V = Q - R где Q а также R точки на поверхности, то если вы преобразуете объект B:
V' = BQ - BR
= B(Q - R)
= BV
Та же логика применима для неплоских поверхностей с учетом ограничений.
В этом случае предположим, что вы намереваетесь преобразовать модель по матрице B, Так B будет применяться к геометрии. Затем, чтобы выяснить, что делать с нормалями, которые нужно найти для матрицы, A чтобы:
(AN)·(BV) = 0
Превращение в строку по сравнению со столбцом, чтобы исключить явный точечный продукт:
[tranpose(AN)](BV) = 0
Вытащите транспонированную наружу, снимите скобки:
transpose(N)*transpose(A)*B*V = 0
Так что это "транспонирование нормального" [продукт с] "транспонирование известной матрицы преобразования" [продукт с] "преобразование, которое мы решаем для" [продукта с] "вектора на поверхности модели" = 0
Но мы начали с того, что transpose(N)*V = 0так как это то же самое, что сказать N·V = 0, Таким образом, чтобы удовлетворить наши ограничения, нам нужна средняя часть выражения - transpose(A)*B - уходить.
Отсюда можно сделать вывод, что:
transpose(A)*B = identity
=> transpose(A) = identity*inverse(B)
=> transpose(A) = inverse(B)
=> A = transpose(inverse(B))
Мое любимое доказательство ниже, где N - нормаль, а V - касательный вектор. Поскольку они перпендикулярны, их скалярное произведение равно нулю. М - любое обратимое преобразование 3х3 (М-1 * М = I). N'и V' - векторы, преобразованные М.
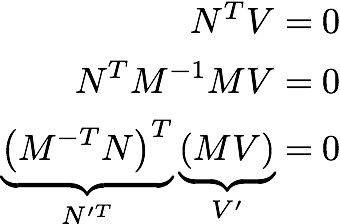
Чтобы получить некоторую интуицию, рассмотрим преобразование сдвига ниже.
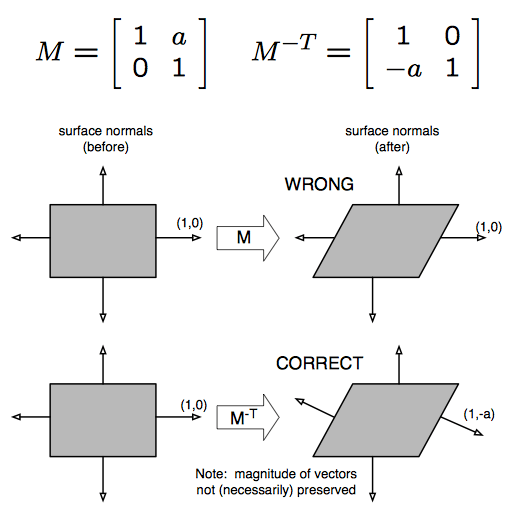
Обратите внимание, что это не относится к касательным векторам.
Если матрица модели состоит из сдвига, поворота и масштаба, вам не нужно делать обратное транспонирование для вычисления нормальной матрицы. Просто разделите нормаль по квадрату масштаба и умножьте на матрицу модели, и все готово. Вы можете распространить это на любую матрицу с перпендикулярными осями, просто вычислите масштаб квадрата для каждой оси матрицы, которую вы используете вместо этого.
Я написал подробности в своем блоге: https://lxjk.github.io/2017/10/01/Stop-Using-Normal-Matrix.html
Не понимаю, почему вы просто не обнуляете 4-й элемент вектора направления перед умножением на матрицу модели. Нет обратного или транспонирования не требуется. Думайте о векторе направления как о разнице между двумя точками. Переместите две точки с остальной частью модели - они все еще находятся в той же относительной позиции к модели. Возьмите разницу между двумя точками, чтобы получить новое направление, и четвертый элемент обнуляется. Намного дешевле.