Превращение цилиндра в сферу без защемления на полюсах
Я работаю над созданием планеты из шестиугольной сетки. Поляки не нужны - сделать это немного проще. Есть ли лучший способ превратить цилиндр в сферу, которая будет иметь однородные шестиугольники / треугольники?
Вот нужные шаги:
- Генерация 2D плоскости шестиугольников (ок)
- Преврати самолет в цилиндр (ок)
- Превратить Цилиндр в Сферу / Геосферу (вид работ)
На втором этапе я просто использую Sin и Cos, чтобы переместить вершины в круглую форму. Для шага 3, сейчас я просто использую: vertices[i] = vertices[i].normalized * radius;
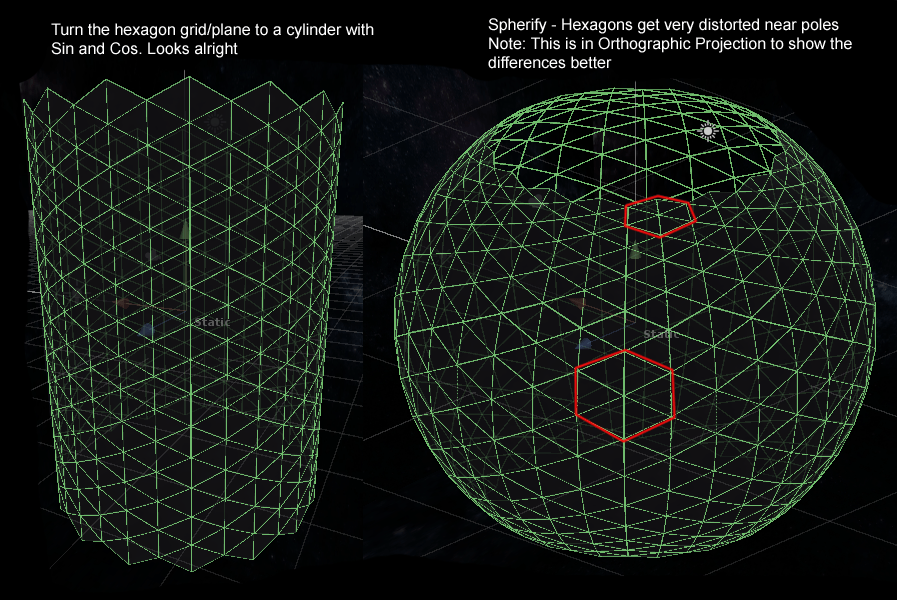
Изображение, чтобы визуализировать проблему, как это в настоящее время.
Обратите внимание, что полюса обрезаны специально. Красные части показывают, как выглядит одна шестигранная сетка. Мне бы пришлось оставить их примерно одинакового размера и ориентации, поскольку они используются для игрового процесса и визуальных элементов. Каждый гекс имеет список соседей и в основном работает как график.
1 ответ
Вместо отображения цилиндра на сферу я бы сделал триангуляцию сферы...
Я бы сначала начал с 2 шестиугольников
каждый начинается на полюсе и заканчивается на экваторе или делает только половину и отражает другое, когда все сделано...
затем рекурсивно поделить треугольники
поэтому разделите линии на половину и измените координату средней точки, чтобы выровнять ее по поверхности сферы. Это создаст триангулированную сферу. Разделите на правильное количество точек, чтобы сформировать шестиугольники и иметь достаточно точек сетки.
изменить координаты средней точки шестиугольника обратно на плоскость шестиугольника
Итак, возьмите остальные 6 точек и вычислите средние координаты, которые дают вам точку для среднего...
Что-то вроде этого:
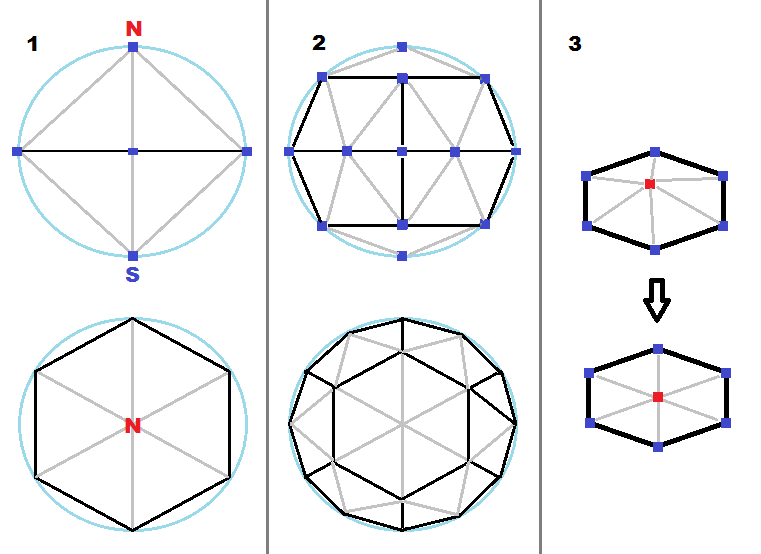
для большего количества идей смотрите здесь:
[edit1] триангуляция (без шестигранных исправлений)
//---------------------------------------------------------------------------
#include <math.h>
#include "list.h"
class mesh
{
public:
class _pnt { public: double p[3]; _pnt(){}; _pnt(_pnt& a){ *this=a; }; ~_pnt(){}; _pnt* operator = (const _pnt *a) { *this=*a; return this; }; /*_pnt* operator = (const _pnt &a) { ...copy... return this; };*/ };
class _fac { public: int i0,i1,i2; _fac(){}; _fac(_fac& a){ *this=a; }; ~_fac(){}; _fac* operator = (const _fac *a) { *this=*a; return this; }; /*_fac* operator = (const _fac &a) { ...copy... return this; };*/ };
List<_pnt> pnt; // mesh points
List<_fac> fac; // mesh triangles
mesh() {}
mesh(mesh& a) { *this=a; }
~mesh() {}
mesh* operator = (const mesh *a) { *this=*a; return this; }
//mesh* operator = (const mesh &a) { ...copy... return this; }
void draw(); // draws the mesh with OpenGL
void sphere(int n); // init mesh with unit sphere from triangles (n recursion layers)
};
//---------------------------------------------------------------------------
void mesh::draw()
{
int i;
_fac *f;
// fill
glColor3f(0.7,0.7,0.7);
glEnable(GL_DEPTH_TEST);
glEnable(GL_CULL_FACE);
glDepthFunc(GL_LEQUAL);
glBegin(GL_TRIANGLES);
for (i=0,f=fac.dat;i<fac.num;i++,f++)
{
glVertex3dv(pnt.dat[f->i0].p);
glVertex3dv(pnt.dat[f->i1].p);
glVertex3dv(pnt.dat[f->i2].p);
}
glEnd();
// wireframe
glColor3f(0.1,0.3,0.7);
glLineWidth(2.0);
for (i=0,f=fac.dat;i<fac.num;i++,f++)
{
glBegin(GL_LINE_LOOP);
glVertex3dv(pnt.dat[f->i0].p);
glVertex3dv(pnt.dat[f->i1].p);
glVertex3dv(pnt.dat[f->i2].p);
glEnd();
}
glLineWidth(1.0);
}
//---------------------------------------------------------------------------
void mesh::sphere(int n)
{
// init 2 hexagons
int i,j,m,i0,i1,i2,j0,j1,j2;
double a,da=M_PI/3.0;
double *p0,*p1;
_pnt p;
_fac f,*g;
p.p[0]= 0.0;
p.p[1]= 0.0;
p.p[2]=+1.0;
pnt.add(p);
p.p[2]=-1.0;
pnt.add(p);
for (i=0,a=0.0;i<6;i++,a+=da)
{
p.p[0]=cos(a);
p.p[1]=sin(a);
p.p[2]= 0.0;
pnt.add(p);
}
// top half
f.i0=0; f.i1=2; f.i2=3; fac.add(f);
f.i0=0; f.i1=3; f.i2=4; fac.add(f);
f.i0=0; f.i1=4; f.i2=5; fac.add(f);
f.i0=0; f.i1=5; f.i2=6; fac.add(f);
f.i0=0; f.i1=6; f.i2=7; fac.add(f);
f.i0=0; f.i1=7; f.i2=2; fac.add(f);
// botom half
f.i0=1; f.i1=3; f.i2=2; fac.add(f);
f.i0=1; f.i1=4; f.i2=3; fac.add(f);
f.i0=1; f.i1=5; f.i2=4; fac.add(f);
f.i0=1; f.i1=6; f.i2=5; fac.add(f);
f.i0=1; f.i1=7; f.i2=6; fac.add(f);
f.i0=1; f.i1=2; f.i2=7; fac.add(f);
// subdivide triangles
for (;n>0;n--) // recursion layers
for (m=fac.num,i=0;i<m;i++)// scan through all original faces
{
g=&fac[i];
// point indexes
i0=g->i0; j0=pnt.num; // i0
i1=g->i1; j1=j0+1; // j0 j2
i2=g->i2; j2=j0+2; // i1 j1 i2
// genere mid points + sphere surface correction distance from (0,0,0) must be 1.0 (radius)
for (j=0;j<3;j++) p.p[j]=0.5*(pnt[i0].p[j]+pnt[i1].p[j]); a=1.0/sqrt((p.p[0]*p.p[0])+(p.p[1]*p.p[1])+(p.p[2]*p.p[2])); for (j=0;j<3;j++) p.p[j]*=a; pnt.add(p);
for (j=0;j<3;j++) p.p[j]=0.5*(pnt[i1].p[j]+pnt[i2].p[j]); a=1.0/sqrt((p.p[0]*p.p[0])+(p.p[1]*p.p[1])+(p.p[2]*p.p[2])); for (j=0;j<3;j++) p.p[j]*=a; pnt.add(p);
for (j=0;j<3;j++) p.p[j]=0.5*(pnt[i2].p[j]+pnt[i0].p[j]); a=1.0/sqrt((p.p[0]*p.p[0])+(p.p[1]*p.p[1])+(p.p[2]*p.p[2])); for (j=0;j<3;j++) p.p[j]*=a; pnt.add(p);
// change original fac
g->i0=j0; g->i1=j1; g->i2=j2;
// add 3 x fac
f.i0=i0; f.i1=j0; f.i2=j2; fac.add(f);
f.i0=j0; f.i1=i1; f.i2=j1; fac.add(f);
f.i0=j2; f.i1=j1; f.i2=i2; fac.add(f);
}
}
//---------------------------------------------------------------------------
Было немного любопытно, поэтому я попытался закодировать это использование просто:
mesh obj; // somewhere global...
obj.sphere(3); // init (call once or on change of n...)
obj.draw(); // inside your gl draw scene routine/event...
Итак, вот обзор результатов
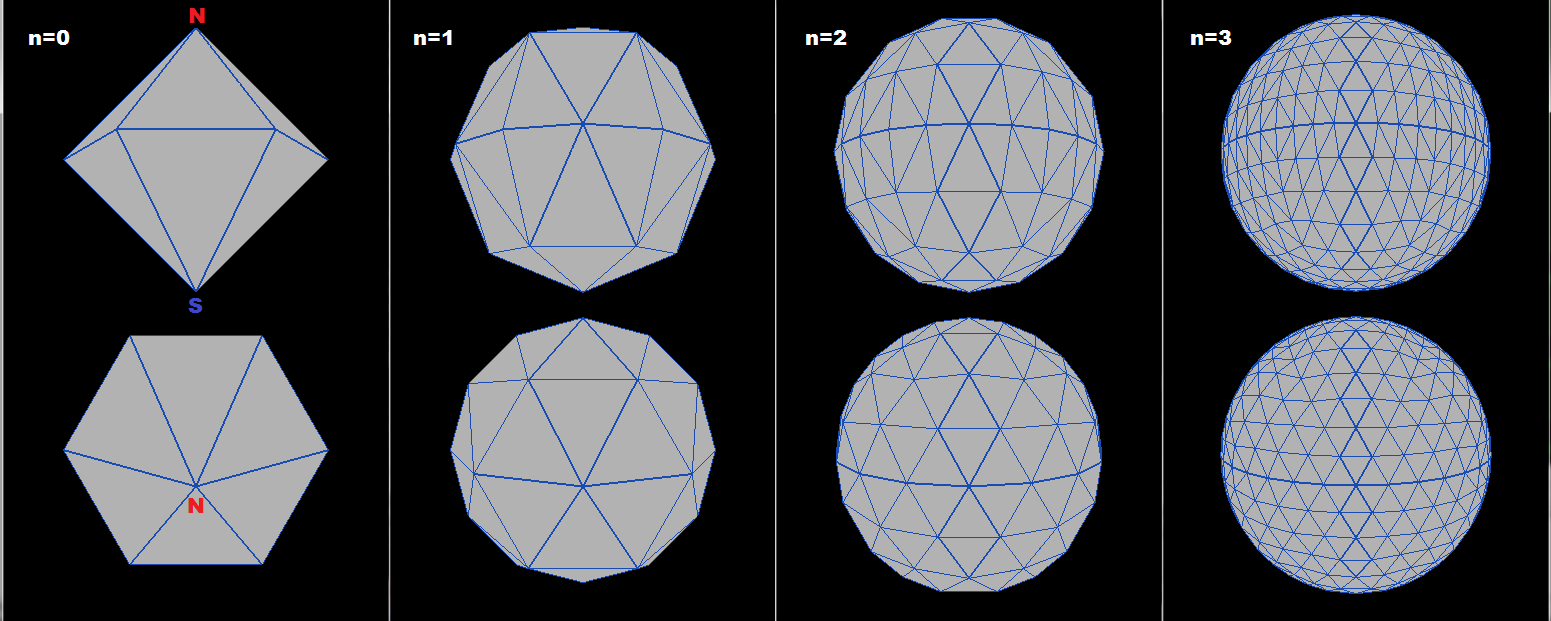
верхний и нижний полюса выглядят достаточно хорошо, вдоль экватора присутствуют некоторые искажения, но частично это может быть вызвано также рыбьим глазом. Если исходная фигура подается с начальной геометрией желаемого результата, то результаты могут быть намного лучше