Расположение самой высокой плотности на сфере
У меня много точек на поверхности сферы. Как я могу рассчитать площадь / точку сферы, которая имеет наибольшую плотность точек? Мне нужно, чтобы это было сделано очень быстро. Например, если бы это был квадрат, я мог бы создать сетку, а затем позволить точкам голосовать, какая часть сетки является лучшей. Я попытался преобразовать точки в сферические координаты, а затем выполнил сетку, и это не сработало, поскольку точки вокруг северного полюса находятся близко к сфере, но далеко после преобразования.
Спасибо
10 ответов
На самом деле нет никакой реальной причины разделять сферу на обычную неперекрывающуюся сетку, попробуйте это:
разделите свою сферу на полуперекрывающиеся круги
см. здесь для генерации равномерно распределенных точек (центры вашего круга)
Вы можете очень быстро определить точки в каждом круге с помощью простого точечного произведения. Это действительно не имеет значения, если некоторые точки подсчитаны дважды, круг с наибольшим количеством точек по-прежнему представляет наибольшую плотность
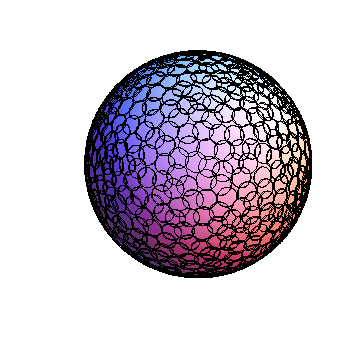
реализация Mathematica
это займет 12 секунд, чтобы проанализировать 5000 баллов. (и заняло около 10 минут, чтобы написать)
testcircles = { RandomReal[ {0, 1}, {3}] // Normalize};
Do[While[ (test = RandomReal[ {-1, 1}, {3}] // Normalize ;
Select[testcircles , #.test > .9 & , 1] ) == {} ];
AppendTo[testcircles, test];, {2000}];
vmax = testcircles[[First@
Ordering[-Table[
Count[ (testcircles[[i]].#) & /@ points , x_ /; x > .98 ] ,
{i, Length[testcircles]}], 1]]];
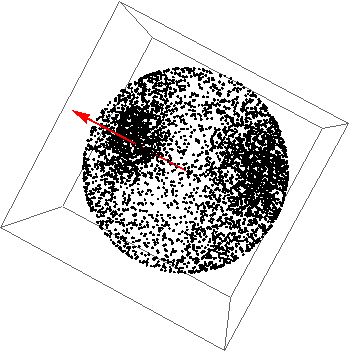
Чтобы добавить некоторые другие альтернативные схемы к смеси: можно определить ряд (почти) регулярных сеток на сферических геометриях, уточнив вписанный многогранник.
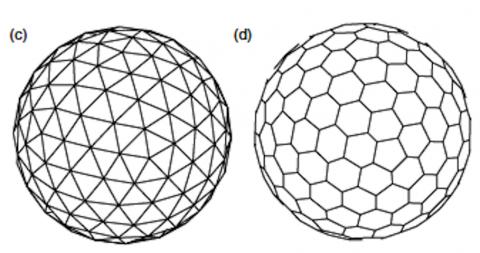
Первый вариант называется икосаэдрической сеткой, которая представляет собой триангуляцию сферической поверхности. Соединяя центры треугольников вокруг каждой вершины, вы также можете создать двойную гексагональную сетку, основанную на базовой триангуляции:
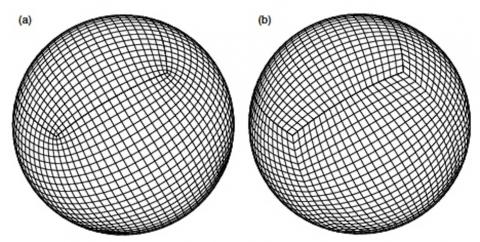
Другой вариант, если вам не нравятся треугольники (и / или шестиугольники), это сетка в форме куба, сформированная путем деления граней вписанного куба и проецирования результата на сферическую поверхность:
В любом случае, важным моментом является то, что полученные сетки являются почти регулярными - поэтому, чтобы оценить область наибольшей плотности на сфере, вы можете просто выполнить анализ в виде гистограммы, подсчитав количество выборок на ячейку сетки.
Как указывалось рядом комментаторов, чтобы учесть небольшую неравномерность в сетке, можно нормализовать количество гистограмм путем деления на площадь каждой ячейки сетки. Результирующая плотность затем дается как мера "на единицу площади". Для вычисления площади каждой ячейки сетки есть два варианта: (i) вы можете рассчитать "плоскую" площадь каждой ячейки, предполагая, что края являются прямыми линиями - такое приближение, вероятно, довольно хорошо, когда сетка достаточно плотный, или (ii) вы можете вычислить "истинные" площади поверхности, оценивая необходимые поверхностные интегралы.
Если вы заинтересованы в эффективном выполнении требуемых запросов "точка-в-ячейке", один из подходов состоит в том, чтобы построить сетку в виде квадродерева - начиная с грубого многогранника с надписью и уточняя его грани в дерево подголовок. Чтобы найти вмещающую ячейку, вы можете просто пройти по дереву от корня, который обычно O(log(n)) операция.
Вы можете получить дополнительную информацию об этих типах сетки здесь.
Рассматривать точки на сфере как трехмерные точки не так уж и плохо.
Попробуйте либо:
- Выберите k, выполните приблизительный поиск k-NN в 3D для каждой точки данных или выбранной точки интереса, а затем оцените результат по их расстоянию до точки запроса. Сложность может варьироваться для разных приближенных алгоритмов k-NN.
- Создайте структуру данных с разделением пространства, такую как kd Tree, затем выполните приблизительный (или точный) запрос подсчета диапазонов с диапазоном шаров, центрированным в каждой точке данных или выбранной точке интереса. Сложность составляет O(log(n) + epsilon^(-3)) или O(epsilon^(-3)*log(n)) для каждого приблизительного запроса диапазона с современными алгоритмами, где epsilon - порог ошибки диапазона по размеру шара запроса. Для точного диапазона запроса сложность O(n^(2/3)) для каждого запроса.
Разделите сферу на равные области (ограниченные параллелями и меридианами), как описано в моем ответе, и подсчитайте точки в каждой области.
Соотношение сторон регионов не будет одинаковым (экваториальные регионы будут более "квадратными", когда N~M, в то время как полярные регионы будут более вытянутыми). Это не проблема, потому что диаметры областей равны 0, так как N а также M увеличение. Простота вычислений этого метода превосходит лучшую однородность областей в других превосходных ответах, которые содержат красивые картинки.
Одной простой модификацией будет добавление двух областей "полярной шапки" к N*M области, описанные в связанном ответе, для улучшения числовой стабильности (когда точка очень близка к полюсу, ее долгота не является четко определенной). Таким образом, пропорции регионов ограничены.
Вы можете использовать проекцию Петерса, которая сохраняет области.
Это позволит вам эффективно подсчитывать точки в сетке, а также в скользящем окне (окно Parzen), используя встроенный трюк с изображением.
Если вам нужна радиальная область наибольшей плотности, это задача надежного покрытия диска сk = 1иdist(a, b) = great circle distance (a, b)(см. https://en.wikipedia.org/wiki/Great-circle_distance )
https://www4.comp.polyu.edu.hk/~csbxiao/paper/2003%20and%20before/PDCS2003.pdf
Это действительно только обратный ответ моего ответа
просто инвертируйте уравнения эквидистантных сферных поверхностных вершин в поверхностный индекс ячейки. Даже не пытайтесь визуализировать ячейку иначе, чем круг, или вы сходите с ума. Но если кто-то действительно сделает это, пожалуйста, опубликуйте результат здесь (и позвольте мне сейчас)
Теперь просто создайте 2D-карту ячеек и выполните расчет плотности в O(N) (как гистограммы сделаны) похоже на то, что Даррен Энгвирда предлагает в своем ответе
Вот так выглядит код в C++
//---------------------------------------------------------------------------
const int na=16; // sphere slices
int nb[na]; // cells per slice
const int na2=na<<1;
int map[na][na2]; // surface cells
const double da=M_PI/double(na-1); // latitude angle step
double db[na]; // longitude angle step per slice
// sherical -> orthonormal
void abr2xyz(double &x,double &y,double &z,double a,double b,double R)
{
double r;
r=R*cos(a);
z=R*sin(a);
y=r*sin(b);
x=r*cos(b);
}
// sherical -> surface cell
void ab2ij(int &i,int &j,double a,double b)
{
i=double(((a+(0.5*M_PI))/da)+0.5);
if (i>=na) i=na-1;
if (i< 0) i=0;
j=double(( b /db[i])+0.5);
while (j< 0) j+=nb[i];
while (j>=nb[i]) j-=nb[i];
}
// sherical <- surface cell
void ij2ab(double &a,double &b,int i,int j)
{
if (i>=na) i=na-1;
if (i< 0) i=0;
a=-(0.5*M_PI)+(double(i)*da);
b= double(j)*db[i];
}
// init variables and clear map
void ij_init()
{
int i,j;
double a;
for (a=-0.5*M_PI,i=0;i<na;i++,a+=da)
{
nb[i]=ceil(2.0*M_PI*cos(a)/da); // compute actual circle cell count
if (nb[i]<=0) nb[i]=1;
db[i]=2.0*M_PI/double(nb[i]); // longitude angle step
if ((i==0)||(i==na-1)) { nb[i]=1; db[i]=1.0; }
for (j=0;j<na2;j++) map[i][j]=0; // clear cell map
}
}
//---------------------------------------------------------------------------
// this just draws circle from point x0,y0,z0 with normal nx,ny,nz and radius r
// need some vector stuff of mine so i did not copy the body here (it is not important)
void glCircle3D(double x0,double y0,double z0,double nx,double ny,double nz,double r,bool _fill);
//---------------------------------------------------------------------------
void analyse()
{
// n is number of points and r is just visual radius of sphere for rendering
int i,j,ii,jj,n=1000;
double x,y,z,a,b,c,cm=1.0/10.0,r=1.0;
// init
ij_init(); // init variables and map[][]
RandSeed=10; // just to have the same random points generated every frame (do not need to store them)
// generate draw and process some random surface points
for (i=0;i<n;i++)
{
a=M_PI*(Random()-0.5);
b=M_PI* Random()*2.0 ;
ab2ij(ii,jj,a,b); // cell corrds
abr2xyz(x,y,z,a,b,r); // 3D orthonormal coords
map[ii][jj]++; // update cell density
// this just draw the point (x,y,z) as line in OpenGL so you can ignore this
double w=1.1; // w-1.0 is rendered line size factor
glBegin(GL_LINES);
glColor3f(1.0,1.0,1.0); glVertex3d(x,y,z);
glColor3f(0.0,0.0,0.0); glVertex3d(w*x,w*y,w*z);
glEnd();
}
// draw cell grid (color is function of density)
for (i=0;i<na;i++)
for (j=0;j<nb[i];j++)
{
ij2ab(a,b,i,j); abr2xyz(x,y,z,a,b,r);
c=map[i][j]; c=0.1+(c*cm); if (c>1.0) c=1.0;
glColor3f(0.2,0.2,0.2); glCircle3D(x,y,z,x,y,z,0.45*da,0); // outline
glColor3f(0.1,0.1,c ); glCircle3D(x,y,z,x,y,z,0.45*da,1); // filled by bluish color the more dense the cell the more bright it is
}
}
//---------------------------------------------------------------------------
Результат выглядит так:

так что теперь просто посмотрим, что в map[][] В массиве вы можете найти глобальную / локальную минимальную / максимальную плотность или все, что вам нужно... Только не забывайте, что размер map[na][nb[i]] где i это первый индекс в массиве. Размер сетки контролируется na постоянная и cm это просто плотность к цветовой гамме...
[edit1] получил сетку Quad, которая является намного более точным представлением используемого отображения
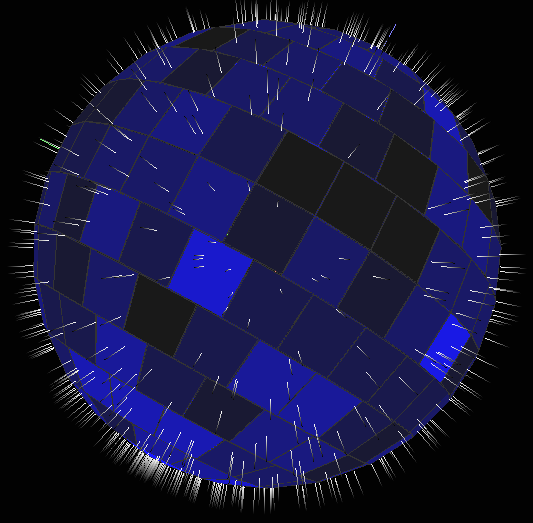
это с na=16 худшие ошибки округления на полюсах. Если вы хотите быть точным, то вы можете взвешивать плотность по размеру поверхности клетки. Для всех неполюсных ячеек это простой квад. Для полюсов свой треугольный веер (правильный многоугольник)
Это код отрисовки сетки:
// draw cell quad grid (color is function of density)
int i,j,ii,jj;
double x,y,z,a,b,c,cm=1.0/10.0,mm=0.49,r=1.0;
double dx=mm*da,dy;
for (i=1;i<na-1;i++) // ignore poles
for (j=0;j<nb[i];j++)
{
dy=mm*db[i];
ij2ab(a,b,i,j);
c=map[i][j]; c=0.1+(c*cm); if (c>1.0) c=1.0;
glColor3f(0.2,0.2,0.2);
glBegin(GL_LINE_LOOP);
abr2xyz(x,y,z,a-dx,b-dy,r); glVertex3d(x,y,z);
abr2xyz(x,y,z,a-dx,b+dy,r); glVertex3d(x,y,z);
abr2xyz(x,y,z,a+dx,b+dy,r); glVertex3d(x,y,z);
abr2xyz(x,y,z,a+dx,b-dy,r); glVertex3d(x,y,z);
glEnd();
glColor3f(0.1,0.1,c );
glBegin(GL_QUADS);
abr2xyz(x,y,z,a-dx,b-dy,r); glVertex3d(x,y,z);
abr2xyz(x,y,z,a-dx,b+dy,r); glVertex3d(x,y,z);
abr2xyz(x,y,z,a+dx,b+dy,r); glVertex3d(x,y,z);
abr2xyz(x,y,z,a+dx,b-dy,r); glVertex3d(x,y,z);
glEnd();
}
i=0; j=0; ii=i+1; dy=mm*db[ii];
ij2ab(a,b,i,j); c=map[i][j]; c=0.1+(c*cm); if (c>1.0) c=1.0;
glColor3f(0.2,0.2,0.2);
glBegin(GL_LINE_LOOP);
for (j=0;j<nb[ii];j++) { ij2ab(a,b,ii,j); abr2xyz(x,y,z,a-dx,b-dy,r); glVertex3d(x,y,z); }
glEnd();
glColor3f(0.1,0.1,c );
glBegin(GL_TRIANGLE_FAN); abr2xyz(x,y,z,a ,b ,r); glVertex3d(x,y,z);
for (j=0;j<nb[ii];j++) { ij2ab(a,b,ii,j); abr2xyz(x,y,z,a-dx,b-dy,r); glVertex3d(x,y,z); }
glEnd();
i=na-1; j=0; ii=i-1; dy=mm*db[ii];
ij2ab(a,b,i,j); c=map[i][j]; c=0.1+(c*cm); if (c>1.0) c=1.0;
glColor3f(0.2,0.2,0.2);
glBegin(GL_LINE_LOOP);
for (j=0;j<nb[ii];j++) { ij2ab(a,b,ii,j); abr2xyz(x,y,z,a-dx,b+dy,r); glVertex3d(x,y,z); }
glEnd();
glColor3f(0.1,0.1,c );
glBegin(GL_TRIANGLE_FAN); abr2xyz(x,y,z,a ,b ,r); glVertex3d(x,y,z);
for (j=0;j<nb[ii];j++) { ij2ab(a,b,ii,j); abr2xyz(x,y,z,a-dx,b+dy,r); glVertex3d(x,y,z); }
glEnd();
mm размер ячейки сетки mm=0.5 полный размер ячейки, меньше создает пространство между ячейками
Я не магистр математики, но, может быть, это можно решить аналитическим путем, как:
1. короткая координата
2.R=(Σ(n=0. N =max)(Σ(m=0. M=n)(1/A^diff_in_consecative))* угол) / Σangle
A = может любая константа
Если я правильно понимаю, вы пытаетесь найти плотную точку на сфере.
если точки плотнее в какой-то момент
Рассмотрим декартовы координаты и найдите среднее значение X,Y,Z точек
Найдите ближайшую точку для обозначения X,Y,Z, которая находится на сфере (вы можете рассмотреть возможность использования сферических координат, просто увеличьте радиус до исходного радиуса).
Ограничения
- Если расстояние между средними значениями X,Y,Z и центром меньше r/2, то этот алгоритм может работать не так, как хотелось бы.
Рассмотрите возможность использования географического метода для решения этой проблемы. Инструменты ГИС, типы данных географии в SQL и т. Д. Все обрабатывают кривизну сфероида. Возможно, вам придется найти систему координат, которая использует чистую сферу вместо земного сфероида, если вы на самом деле не моделируете что-то на Земле.
Для скорости, если у вас есть большое количество точек и вы хотите их наиболее плотное расположение, решение типа растровой тепловой карты может работать хорошо. Вы можете создавать растры с низким разрешением, затем увеличивать области с высокой плотностью и создавать только те ячейки с более высоким разрешением, которые вам нужны.