Как вы находите положение Y точки между четырьмя вершинами? HLSL

Question

Допустим, в игре есть сетка ландшафта, состоящая из плиток, состоящих из двух треугольников - из четырех вершин. Как бы мы нашли положение Y (вверх) точки между четырьмя вершинами?

Я попробовал это:

float diffZ1    = lerp(heights[0], heights[2], zOffset);
float diffZ2    = lerp(heights[1], heights[3], zOffset);
float yPosition = lerp(diffZ1, diffZ2, xOffset);

Где z/yOffset - это смещение z / y от первой вершины тайла в процентах / 100. Это работает для плоских поверхностей, но не очень хорошо на неровной местности.

Я ожидаю, что это как-то связано с рельефом местности из треугольников, где вышеперечисленное может работать на плоских плоскостях. Я не уверен, но кто-нибудь знает, что происходит не так?

Это может лучше объяснить, что здесь происходит:

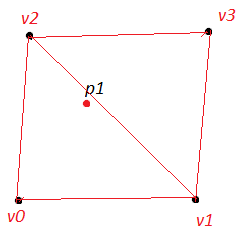
В приведенном выше коде "heights[]" представляет собой массив координат Y окружающих вершин v0-3. Треугольник 1 состоит из вершин 0, 2 и 1. Треугольник 2 состоит из вершин 1, 2 и 3.

Я хочу найти координату Y для p1, когда его координаты x,y лежат между v0-3.

Итак, я попытался определить, между каким треугольником находится точка, с помощью этой функции:

bool PointInTriangle(float3 pt, float3 pa, float3 pb, float3 pc)
{
  // Compute vectors        
  float2 v0 = pc.xz - pa.xz;
  float2 v1 = pb.xz - pa.xz;
  float2 v2 = pt.xz - pa.xz;

  // Compute dot products
  float dot00 = dot(v0, v0);
  float dot01 = dot(v0, v1);
  float dot02 = dot(v0, v2);
  float dot11 = dot(v1, v1);
  float dot12 = dot(v1, v2);

  // Compute barycentric coordinates
  float invDenom = 1.0f / (dot00 * dot11 - dot01 * dot01);
  float u = (dot11 * dot02 - dot01 * dot12) * invDenom;
  float v = (dot00 * dot12 - dot01 * dot02) * invDenom;

  // Check if point is in triangle
  return (u >= 0.0f) && (v >= 0.0f) && (u + v <= 1.0f);
}

Это не дает мне ожидаемых результатов

Затем я пытаюсь найти координату y точки p1 внутри каждого треугольника:

// Position of point p1
float3 pos = input[0].PosI;

// Calculate point and normal for triangles
float3 p1 = tile[0];
float3 n1 = (tile[2] - p1) * (tile[1] - p1); // <-- Error, cross needed
       // = cross(tile[2] - p1, tile[1] - p1);
float3 p2 = tile[3];
float3 n2 = (tile[2] - p2) * (tile[1] - p2);  // <-- Error
       // = cross(tile[2] - p2, tile[1] - p2); 
float newY = 0.0f;

// Determine triangle & get y coordinate inside correct triangle
if(PointInTriangle(pos, tile[0], tile[1], tile[2]))
{
    newY = p1.y - ((pos.x - p1.x) * n1.x + (pos.z - p1.z) * n1.z) / n1.y;
}
else if(PointInTriangle(input[0].PosI, tile[3], tile[2], tile[1]))
{
    newY = p2.y - ((pos.x - p2.x) * n2.x + (pos.z - p2.z) * n2.z) / n2.y;
}

---

Используя следующее, чтобы найти правильный треугольник:

if((1.0f - xOffset) <= zOffset)
    inTri1 = true;

И исправление приведенного выше кода для использования правильной перекрестной функции, похоже, решило проблему.

Answer 1

Поскольку ваши 4 вершины могут не находиться на плоскости, вы должны рассматривать каждый треугольник отдельно. Сначала найдите треугольник, в котором находится точка, а затем используйте следующее обсуждение Stackru, чтобы найти значение Z (обратите внимание на различное именование осей). Мне лично ответ Даниэлко нравится гораздо лучше, но принятый ответ тоже должен сработать:

Линейная интерполяция трех трехмерных точек в трехмерном пространстве

---

РЕДАКТИРОВАТЬ: Для 2-й части вашей проблемы (нахождение треугольника, в котором находится точка): поскольку проекция ваших плиток на плоскость xz (как вы определяете свои координаты) являются идеальными квадратами, нахождение треугольника, в котором находится точка, очень простая операция. Здесь я буду использовать термины влево-вправо для обозначения оси x (от более низких до более высоких значений x) и снизу вверх для обозначения оси z (от более низких до более высоких значений z).

Каждая плитка может быть разделена только одним из двух способов. Либо (A) через диагональную линию из нижнего левого угла в верхний правый угол, либо (B) через диагональную линию из нижнего правого угла в верхний левый угол.

• Для любой плитки, которая разделена как A: проверьте, если x' > z', где x '- расстояние от левого края плитки до точки, а z' - расстояние от нижнего края плитки до точки. Если x' > z', то ваша точка находится в нижнем правом треугольнике; в противном случае это в верхнем левом треугольнике.

• Для любой плитки, которая разделена как B: проверьте, если x" > z', где x" - расстояние от правого края плитки до точки, а z' - расстояние от нижнего края плитки до точки. Если x" > z', то ваша точка находится в нижнем левом треугольнике, в противном случае она находится в верхнем правом треугольнике.

(Небольшое примечание: выше я предполагаю, что ваши плитки не вращаются в плоскости xz; то есть, что они выровнены с осями. Если это не правильно, просто поверните их, чтобы выровнять их с осями, прежде чем выполнять вышеуказанные проверки.)