Как найти лучшую прямую линию, разделяющую две области, имеющие точки с двумя разными свойствами

Question

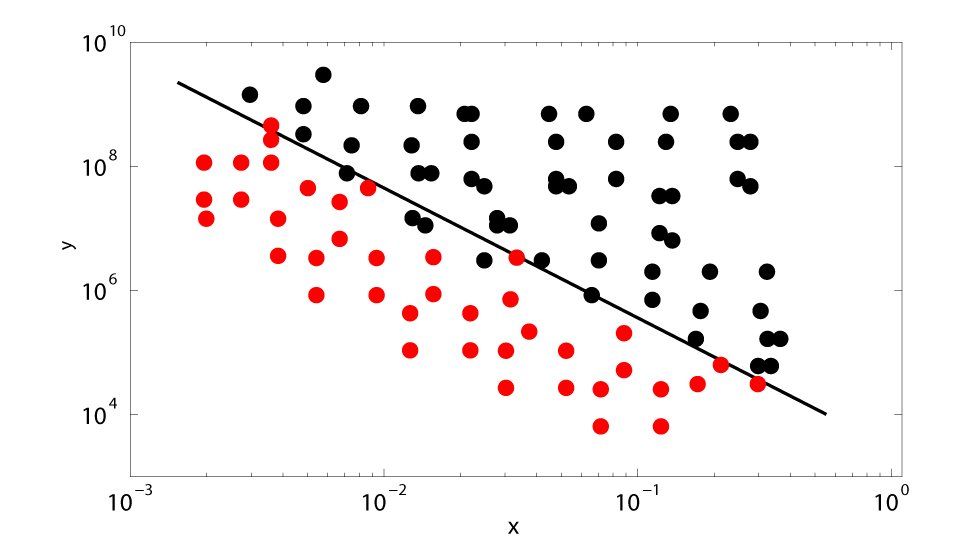
У меня есть куча точек на 2D-графике. Красные точки показывают, когда мой эксперимент стабилен, а черные - нестабильны. Эти две области четко разделены линией на этом графике log-log, и я хотел бы найти лучшую "разделительную линию", то есть линию, которая дает критерий для разделения 2 областей и имеет минимальную ошибку по этому критерию. Я выполнил поиск по различным книгам и в Интернете, но не смог найти никакого подхода к решению этой проблемы. Вы знаете какой-нибудь инструмент? Прежде всего нужно определить ошибку. Одна вещь, которая приходит мне в голову: если неизвестная линия является ax+by+c=0, для каждой точки (x0,y0) мы определяем функцию ошибки, как показано ниже:

E=0 if point lays on the correct side of the line.
E= distance(a*x+b*y+c=0,(x0,y0)) = |a*x0+b*y0+c|/sqrt(a^2+b^2)   if the point
   lies on the wrong side.

и мы минимизируем сумму ошибок. Не просто, так как порог есть. Если вы, ребята, знаете о каких-либо ссылках или ссылках подходов, которые решают эту проблему, это будет оценено. Приветствия А.

Answer 1

Некоторые ссылки: Википедия Линейный классификатор и Машина опорных векторов (SVM),
scikit-learn SVM, пример с 3 классами,
вопросы / теги / классификация по SO,
Еще 3000 вопросов / с тегами / классификация на stats.stackexchange,
Еще 400 вопросов / с тегами / классификация на datascience.stackexchange.

Для вашей задачи 2 класса, выполните следующие действия:

1. найти середины Rmid красных точек, Bmid черных, Mid of the lot

2. провести линию L от Rmid до Bmid

3. (гипер) плоскость через середину, перпендикулярную линии L, это то, что вы хотите: линейный классификатор.
   Или вы можете просто сравнить расстояния | х - Rmid| и |x - Bmid|: вызвать x ближе к Rmid red, ближе к Bmid black.

Но это еще не все. Проецирование всех точек данных на линию L дает одномерную задачу:

rrrrrrrrrrbrrrrrrrrbbrrr | rrbbbbbbbbbbbbbbb

Это хорошая идея, чтобы наметить все точки на этой линии, чтобы увидеть и лучше понять данные.
(Для облаков точек, скажем, в 5 или 10 измерениях, было бы забавно и / или информативно смотреть на 2d или 3d срезы под разными углами.)

Каждый разрез, "|" выше, дает "матрицу путаницы" из 4 чисел:

R-correct   R-called-B  e.g.  490   10
B-called-R  B-correct          50  450

Это дает приблизительное представление о частоте ошибок ваших прогнозов: красный / черный; распечатай, обсуди.
Наилучшее сокращение зависит от затрат, например, если вызов R a B в 10 или 100 раз хуже, чем вызов B a R.

Если красные точки и черные точки имеют разный разброс / ковариацию, см . Линейный дискриминант Фишера.

("SVM" - это жаргон для класса методов "хорошего" разделения гиперплоскостей / гиперповерхностей - здесь нет "машины".)