Вычисление прямоугольной 3D-координаты с координатой его тени?
Иногда возникала проблема в том, что это прямоугольник, повернутый в 3D и являющийся перспективным переходом (например, в CSS) рисовать как четырехугольник. Но мы хотим получить прямоугольник (ширина, длина, угол Эйлера, перспектива), преобразованный с помощью поворота и рисования перспективы в качестве четырехугольника.
2 ответа
Решать:
Система координат:
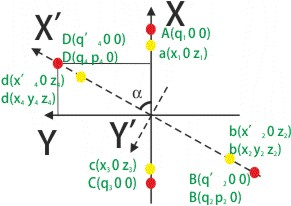
Начало системы координат совпадает с точкой пересечения диагоналей. Топор Z нормальный к четырехугольнику. Топор Х пересекает точку А
a,b,c,d;-;- прямоугольный с координатами
а (х 1, у 1, z 1); b (x 2, y 2, z 2); с (х 3, у 3, z 3); а (х 4, у 4, z 4);
А, В, С,D-тень. Угловые точки A (q 1, p 1, 0); B (q 2, p 2, 0); C (q 3, p 3, 0); D (q 4, p 4, 0);
к перспективе.
В этой системе координат y 1 = y 3 = 0.
Рисунок 1.
Из подобия преобразования треугольников есть:
x 1 = 1-z 1 / k q 1;
x 3 = 1-z 3 / k q 3
Из постановки задачи было то, что диагональный крест находится в начале координат таким образом:
z 3 = -z 1 и x 3 = -x 1
Подставляя в вышеприведенном выражении и приравнивая друг друга, было:
x 1 = 2 * q 1 * q 3 / (q 3 -q 1);
z 1 = (q 1 + q 3) / (q 1 -q 3) * k.
Чтобы упростить другие вычисления, представьте, что диагональ второго прямоугольника (bd) лежит в системе координат, в которой координата Y диагональных точек равна нулю. В этой системе координат точки координат b и d были такими же, как точки a и c, но мы должны изменить z 1 на z 2, z 3 на z 4, x 1 на x 2, x 3 на x 4, q 1 на q 2 q 3 до q 4.
Для перевода из системы воображения в реальную систему используйте формулу координат вращения (Z ax - то же самое, z-координата равна)
Рис.2
X = X '* соз (а); у = у '* Sin (а);
Результат был:
x 2 = -x 4 = 2 * q 2 * q 4 / (q 4 -q 2);
y 2 = -y 4 = x 2 * tan (a);
z 2 = -z 4 = (q 2 + q 4) / (q 2 -q 4) k; tan (a) = (p 2 -p 4) / (q 2 -q 4)
abcd был параллелограммом. Диагональная точка пересечения делит диагональ на половину. Нам нужно еще одно выражение сделать прямоугольным. Используйте угол, равный 90 градусам. Сделать скалярный вектор умножения двух сторон в abcd. По координатам это было:
(ab) (da) = y 4 y 2 + (x 1 -x 4) (x 1 -x 2) + (z 1 -z 4) * (z 1 -z 2) = 0;
f = (q 1 * q 2 -q 3 q 4) (q 1 * q 4 -q 2 * q 3)
g = -tan 2 (a) * q 4 2 q 2 2 (q 1 -q 3) 2 + (- q 1 q 2 (q 3 + q 4) + q 3 q 4 (q 1 + q 2)) * (q 1 q 2 (q 4 -q 3) + q 3 q 4 (q 1 -q 2))
Получаем уравнение к k(в перспективе): f * k 2 -g = 0, решаем его
к = SQRT (г / ж).
Собрав все формулы мы получим все координаты точки abcd.
Из координаты угла легко рассчитать сторону прямоугольника.
Рисунок рис.1 точки a,c диагональный прямоугольник (желтый), точки A,C диагональный четырехугольник (тень) (красный)
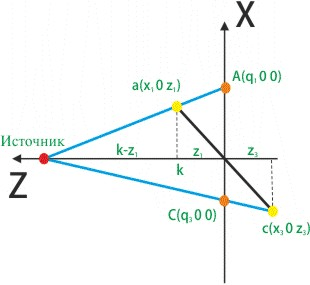
рис.2 a,b,c,d точки прямоугольника (желтый) A,B,C,D тень (четырехугольник) (красный)