Рассчитать кватернион по координате 2 точки объекта в двух позициях

Question

Объект вращается в 3D. У меня есть центр вращения и координата 2 точки в повороте, а не поворот. Рассчитайте кватернионы, которые вращают объект из первой позиции в две позиции.

Answer 1

Мы должны вектор OA 'и OB' в первой позиции объекта
ОА и ОВ на второй позиции
Q векторная часть кватерниона Q ₀ скалярная часть

рисунок 1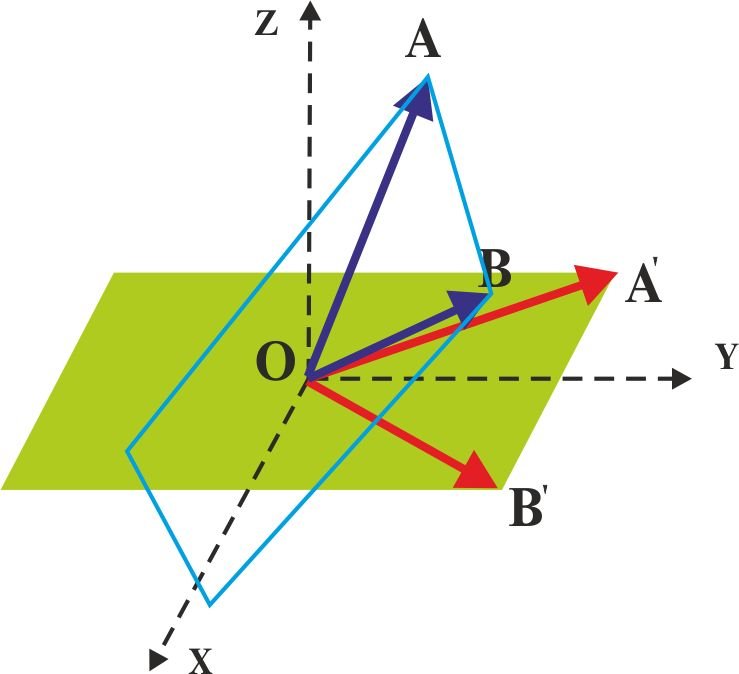
КОММЕНТАРИЙ
OA OB - точечный векторный продукт
OAxOB - кросс-векторное произведение

Кватернион вращения объекта от первого положения ко второму составил:
1 случай
Если OA OB'-OB OA 'не равно нулю, то Q = Q ₀ [(OA-OA') x (OB-OB ')] / [OA * OB'-OA' OB],
где Q ₀ ^-2 = ([(OA-OA ') x (OB-OB')] / [OA OB'-OA ' OB]) ² +1

Если OA OB'-OB OA '= 0, то
2 случая
если [OA '+ OA] x [OB' + OB] не равно нулю, а OB-OB 'не равно нулю,
тогда существуют m, что OA-OA '= m (OB-OB'). Ищите это.
Q = n * (m OB '+ OA'),
где n = Q ₀ (OB-OB ') ² / (2 * OB * [OA'xOB'])
Q ₀ ^-2 = (OB-OB ') ⁴ * (OB' + OA ') ² / (2 * OB * [OA'xOB']) ² +1

Если OA OB'-OB OA '= 0 и [OA + OA'] x [OB + OB '] = 0
3 случая
Если OB + OB не равен нулю, то
Q = (OB + OB ') / | OB + OB' |, Q ₀ = 0 еще

4 случая
OB + OB '= 0
Q = ([OB '] x [OA']) / | [OB '] x [OA'] |, Q ₀ = 0

Из кватерниона мы можем вычислить матрицу вращения или углы Эйлера

Answer 2

Посмотрите на ответ на похожий вопрос. Как найти правильное вращение от одного вектора к другому?

Ваша разница в том, что второй вектор "вверх" не перпендикулярен первому "dir". Просто сделай это и проблема решена