Общий метод вычисления гладких нормалей вершин со 100% гладкостью

Question

Я давно смотрю онлайн и не могу найти ответ на этот вопрос. Для простоты, давайте просто предположим, что мне нужно полностью сгладить нормали группы смежных граней. Я хочу найти фактическую геометрическую биссектрису между группой векторов, игнорируя двойные нормали и поддерживая точность с супами из треугольников. По сути, для этого необходимо:

• Работа с супами из треугольников - будь то три, 4 или 4000 треугольников, нормали все равно должны работать геометрически правильно, без смещения в произвольные области
• Игнорировать перекрывающиеся (параллельные) нормали - если у меня есть ребро куба, которое объединяется в 3 треугольника, или одно, которое объединяется в один треугольник для каждой из двух сторон и 2 (или более) для последней стороны, или то, которое имеет миллион треугольники только на одной стороне, биссектриса не должна меняться

Наиболее распространенная формула для нормального сглаживания, которую я нахожу, заключается в простом усреднении их путем суммирования нормальных векторов и деления на три; пример:

normalize((A + B + C) / 3);

Конечно, деление на три бесполезно, что уже означает атмосферу наивного, грубого усреднения методом грубой силы, который предлагают люди; проблемы с этим также являются тем фактом, что он портит четные треугольные супы и параллельные нормали.

Другое замечание, которое я, похоже, нахожу, состоит в том, чтобы сохранить начальные "фасетные" нормали, поскольку они получены из общей операции умножения, которая их генерирует, так как они (как бы) взвешиваются по площади треугольника. Это может быть чем-то, что вы хотите сделать в некоторых случаях, однако мне нужен чистый биссектриса, поэтому площадь не должна влиять на формулу, и даже учитывая ее, она по-прежнему запутывается в супах треугольника.

Я видел один упомянутый метод, который говорит, что нужно весить против угла между смежными гранями, но я не могу правильно реализовать формулу - либо это, либо он не выполняет то, что я хочу. Однако мне трудно сказать, так как я не могу найти краткое объяснение этому, и мой разум оцепенел от всего этого напрасного мозгового штурма.

Кто-нибудь знает общую формулу? Если это поможет, я работаю с C++ и DirectX11.

---

Изменить: вот несколько похожих вопросов, которые описывают некоторые методы;

• Как добиться гладких касательных пространственных нормалей?
• Вычисление вершинных нормалей сетки
• Вычисление нормалей в треугольной сетке
• Как Blender вычисляет нормали вершин?
• Наиболее эффективный алгоритм вычисления нормалей вершин из набора треугольников для затенения Гуро

Также эта статья: http://www.bytehazard.com/articles/vertnorm.html

К сожалению, реализации, которые я попробовал, не сработали, и я не смог найти четкого и краткого утверждения о том, какая формула на самом деле мне нужна. После некоторых проб и ошибок я наконец понял, что взвешивание по углу было правильным способом сделать это, только я не смог правильно его реализовать; как это сейчас работает, я добавлю свою реализацию в качестве ответа ниже.

Answer 1

Правильный метод - взвешивать "фасетные" нормали к углу между двумя соседними вершинами одной общей в ребре / углу.

(здесь показан угол относительно каждой грани)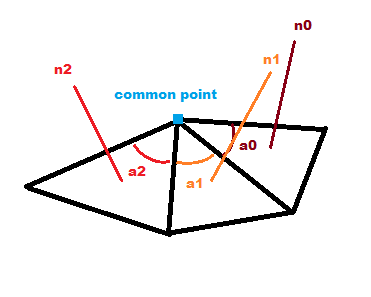

Вот краткое изложение примера реализации:

for (int f = 0; f < tricount; f++)
{
    // ...
    // p1, p2 and p3 are the points in the face (f)

    // calculate facet normal of the triangle using cross product;
    // both components are "normalized" against a common point chosen as the base
    float3 n = (p2 - p1).Cross(p3 - p1);    // p1 is the 'base' here

    // get the angle between the two other points for each point;
    // the starting point will be the 'base' and the two adjacent points will be normalized against it
    a1 = (p2 - p1).Angle(p3 - p1);    // p1 is the 'base' here
    a2 = (p3 - p2).Angle(p1 - p2);    // p2 is the 'base' here
    a3 = (p1 - p3).Angle(p2 - p3);    // p3 is the 'base' here

    // normalize the initial facet normals if you want to ignore surface area
    if (!area_weighting)
    {
        normalize(n);
    }

    // store the weighted normal in an structured array
    v1.wnormals.push_back(n * a1);
    v2.wnormals.push_back(n * a2);
    v3.wnormals.push_back(n * a3);
}
for (int v = 0; v < vertcount; v++)
{
    float3 N;

    // run through the normals in each vertex's array and interpolate them
    // vertex(v) here fetches the data of the vertex at index 'v'
    for (int n = 0; n < vertex(v).wnormals.size(); v++)
    {
        N += vertex(v).wnormals.at(n);
    }

    // normalize the final normal
    normalize(N);
}

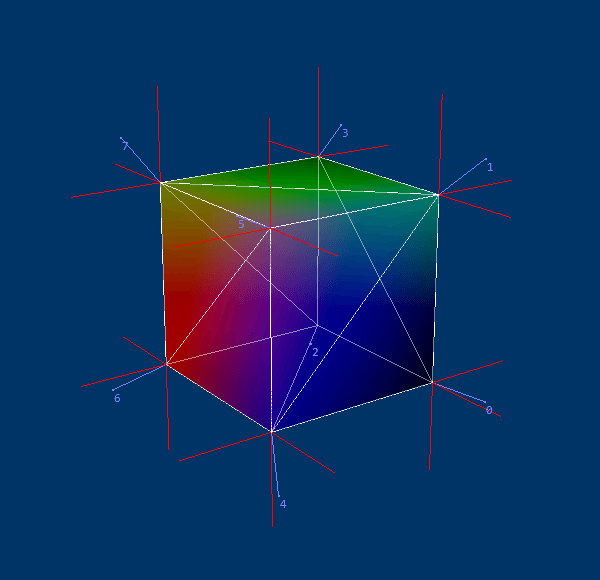
Вот пример "наивного" среднего значения нормалей (т.е. без угловых весов);

Вы можете видеть, что компоненты фасетов одинаковы, но поскольку у некоторых сторон есть две грани, их часть интерполяции удваивается, что делает среднее отклонение. Взвешивание только по площади поверхности, но не по углам, дает аналогичные результаты.

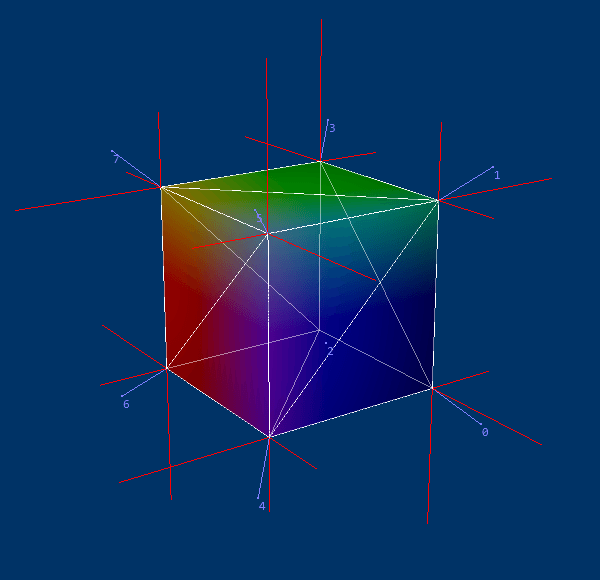
Вместо этого это та же модель, но с включенным угловым взвешиванием;

Теперь все интерполированные нормали являются геометрически правильными.