Повернуть вектор на основе нормального

Question

Дан набор точек на поверхности полусферы, определенной плоскостью XZ в левой системе координат: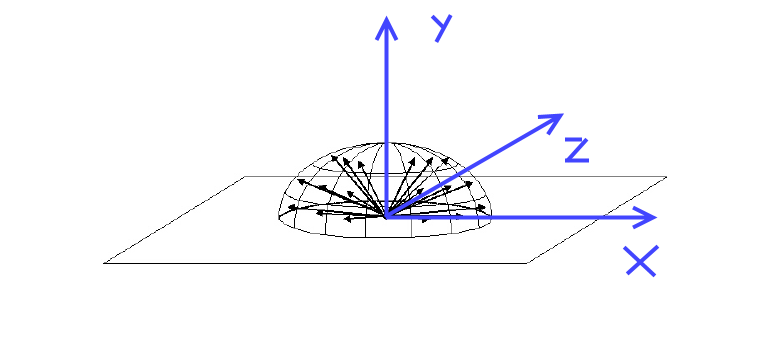

И заданный вектор нормали к плоскости, которая определяет другое произвольное полушарие: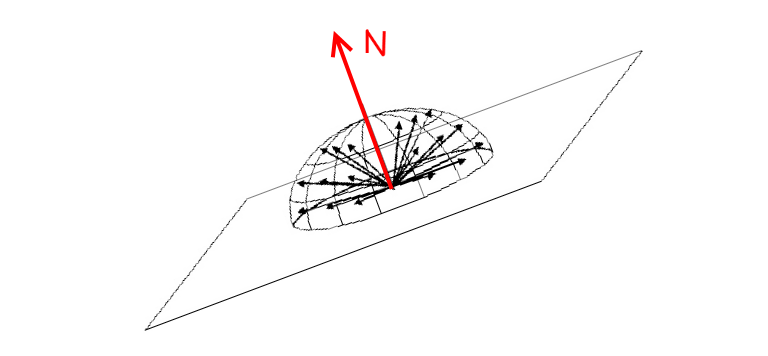

Как определить матрицу вращения, которая позволяет мне преобразовывать каждую точку (вектор) из первого полушария в соответствующую точку во втором полушарии?

Если возможно, было бы удобно иметь матрицу вращения, которая использует сферические координаты N в качестве углов поворота, причем $ \ theta $ - это полярный угол, который переходит от $0$ к $ \ pi $ (интуитивно от Y до -Y) и $\phi$ - азимутальный угол, который идет от $0$ до $2\pi$ (от X обратно к X, проходящему через +Z, -X, -Z).

Answer 1

Первым шагом для построения матрицы вращения является определение последовательности (3) вращения вокруг одной оси. В вашем случае с 2 углами будет достаточно 2 поворота (с фи и тета).

Я всегда ссылаюсь на эту структуру из Википедии. Для использования phi и theta я могу ошибаться (по отношению к вашему соглашению), но я стараюсь быть настолько ясным, насколько могу

Моя личная последовательность могла бы быть: сначала вращение вокруг оси Y угла phi в [0,2pi], которое выравнивает "старые" оси X и Z с "новыми", предполагая, что N параллельно Y. Затем вращение угол тета вокруг оси "новый = уже повернутый" Z, чтобы привести "новую" ось Y вдоль N.

Итак, давайте строить наши матрицы. Вращение вокруг Y имеет эту структуру (я использую; чтобы разбить линии, R всегда 3x3)

R_y = [cos(phi) 0 sin(phi); 0 1 0; -sin(phi) 0 cos(phi)]
R_z = [cos(phi) -sin(phi) 0; sin(phi) cos(phi) 0; 0 0 1]

Полный поворот от старой системы к новой - это произведение двух матриц, помня, какая из них пришла первой

R = R_z*R_y

фактически мы хотим преобразовать набор трехмерных координат a в старую систему, так что это:

b = R*a = R_z*R_y*a = R_z*(R_y*a)   

и вы получите новые координаты б