Фиттинг с ограничениями на производный Python

Question

При попытке создать алгоритм оптимизации мне пришлось наложить ограничения на подгонку кривой моего набора.

Вот моя проблема, у меня есть массив:

Z = [10.3, 10, 10.2, ...]
L = [0, 20, 40, ...]

Мне нужно найти функцию, которая подходит Z с условием наклона, который является производной от функции, которую я ищу.

предполагать f это моя функция, f должен соответствовать Z и иметь условие на f его производная, она не должна превышать специальное значение.

Существуют ли в Python библиотеки, которые могут помочь мне решить эту задачу?

Answer 1

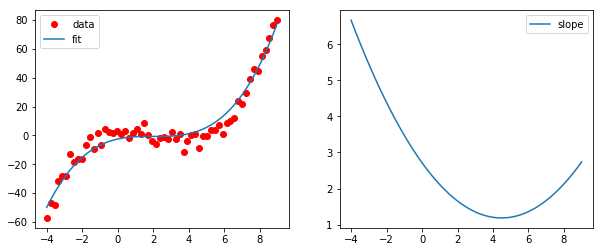
Минимизатор COBYLA может справиться с такими проблемами. В следующем примере полином степени 3 снабжен условием, что производная всюду положительна.

from matplotlib import pylab as plt

import numpy as np
from scipy.optimize import minimize

def func(x, pars):
    a,b,c,d=pars
    return a*x**3+b*x**2+c*x+d

x = np.linspace(-4,9,60)
y = func(x, (.3,-1.8,1,2))
y += np.random.normal(size=60, scale=4.0)

def resid(pars):
    return ((y-func(x,pars))**2).sum()

def constr(pars):
    return np.gradient(func(x,pars))

con1 = {'type': 'ineq', 'fun': constr}
res = minimize(resid, [.3,-1,1,1], method='cobyla', options={'maxiter':50000}, constraints=con1)
print res

f=plt.figure(figsize=(10,4))
ax1 = f.add_subplot(121)
ax2 = f.add_subplot(122)

ax1.plot(x,y,'ro',label='data')
ax1.plot(x,func(x,res.x),label='fit')
ax1.legend(loc=0) 
ax2.plot(x,constr(res.x),label='slope')
ax2.legend(loc=0)
plt.show()

Answer 2

Вот пример подгонки прямой линии с ограничением на производную. Это реализовано в виде простой "кирпичной стены" в устанавливаемой функции, где при превышении максимального значения производной функция возвращает очень большое значение и, следовательно, очень большую ошибку. В примере используется модуль генетического алгоритма дифференциальной эволюции scipy для оценки начальных параметров для подгонки кривой, и, поскольку этот модуль использует алгоритм Латинского гиперкуба для обеспечения тщательного поиска в пространстве параметров, в примере требуются границы параметров, в которых нужно искать - в этом примере эти границы получены из данных максимальных и минимальных значений. Пример завершает подгонку с последним вызовом curve_fit() без передачи границ параметров, в случае, если фактические лучшие параметры находятся за пределами границ, используемых для генетического алгоритма.

Обратите внимание, что окончательно подобранные параметры показывают, что параметр наклона находится на пределе производной, здесь это сделано, чтобы показать, что это может произойти. Я не считаю это условие оптимальным.

import numpy, scipy, matplotlib
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from scipy.optimize import differential_evolution
import warnings

derivativeLimit = 0.0025

xData = numpy.array([19.1647, 18.0189, 16.9550, 15.7683, 14.7044, 13.6269, 12.6040, 11.4309, 10.2987, 9.23465, 8.18440, 7.89789, 7.62498, 7.36571, 7.01106, 6.71094, 6.46548, 6.27436, 6.16543, 6.05569, 5.91904, 5.78247, 5.53661, 4.85425, 4.29468, 3.74888, 3.16206, 2.58882, 1.93371, 1.52426, 1.14211, 0.719035, 0.377708, 0.0226971, -0.223181, -0.537231, -0.878491, -1.27484, -1.45266, -1.57583, -1.61717])
yData = numpy.array([0.644557, 0.641059, 0.637555, 0.634059, 0.634135, 0.631825, 0.631899, 0.627209, 0.622516, 0.617818, 0.616103, 0.613736, 0.610175, 0.606613, 0.605445, 0.603676, 0.604887, 0.600127, 0.604909, 0.588207, 0.581056, 0.576292, 0.566761, 0.555472, 0.545367, 0.538842, 0.529336, 0.518635, 0.506747, 0.499018, 0.491885, 0.484754, 0.475230, 0.464514, 0.454387, 0.444861, 0.437128, 0.415076, 0.401363, 0.390034, 0.378698])


def func(x, slope, offset): # simple straight line function
    derivative = slope # in this case, derivative = slope
    if derivative > derivativeLimit:
        return 1.0E50 # large value gives large error
    return x * slope + offset


# function for genetic algorithm to minimize (sum of squared error)
def sumOfSquaredError(parameterTuple):
    warnings.filterwarnings("ignore") # do not print warnings by genetic algorithm
    val = func(xData, *parameterTuple)
    return numpy.sum((yData - val) ** 2.0)


def generate_Initial_Parameters():
    # min and max used for bounds
    maxX = max(xData)
    minX = min(xData)
    maxY = max(yData)
    minY = min(yData)

    slopeBound = (maxY - minY) / (maxX - minX)

    parameterBounds = []
    parameterBounds.append([-slopeBound, slopeBound]) # search bounds for slope
    parameterBounds.append([minY, maxY]) # search bounds for offset

    # "seed" the numpy random number generator for repeatable results
    result = differential_evolution(sumOfSquaredError, parameterBounds, seed=3)
    return result.x

# by default, differential_evolution completes by calling curve_fit() using parameter bounds
geneticParameters = generate_Initial_Parameters()

# now call curve_fit without passing bounds from the genetic algorithm,
# just in case the best fit parameters are aoutside those bounds
fittedParameters, pcov = curve_fit(func, xData, yData, geneticParameters)
print(fittedParameters)
print()

modelPredictions = func(xData, *fittedParameters) 

absError = modelPredictions - yData

SE = numpy.square(absError) # squared errors
MSE = numpy.mean(SE) # mean squared errors
RMSE = numpy.sqrt(MSE) # Root Mean Squared Error, RMSE
Rsquared = 1.0 - (numpy.var(absError) / numpy.var(yData))

print()
print('RMSE:', RMSE)
print('R-squared:', Rsquared)

print()


##########################################################
# graphics output section
def ModelAndScatterPlot(graphWidth, graphHeight):
    f = plt.figure(figsize=(graphWidth/100.0, graphHeight/100.0), dpi=100)
    axes = f.add_subplot(111)

    # first the raw data as a scatter plot
    axes.plot(xData, yData,  'D')

    # create data for the fitted equation plot
    xModel = numpy.linspace(min(xData), max(xData))
    yModel = func(xModel, *fittedParameters)

    # now the model as a line plot
    axes.plot(xModel, yModel)

    axes.set_xlabel('X Data') # X axis data label
    axes.set_ylabel('Y Data') # Y axis data label

    plt.show()
    plt.close('all') # clean up after using pyplot

graphWidth = 800
graphHeight = 600
ModelAndScatterPlot(graphWidth, graphHeight)