Проверка глубины /z при рендеринге треугольных граней в трехмерном пространстве

Question

Мой вопрос можно упростить до следующего: если трехмерный треугольник проецируется и визуализируется на двухмерную плоскость просмотра, как можно рассчитать значение z каждого визуализируемого пикселя для его сохранения в буфере?

В настоящее время у меня есть работающая Java-программа, которая способна отображать трехмерные треугольники в двухмерный вид в виде сплошного цвета, и камеру можно без проблем перемещать, поворачивать и т. Д., Работая точно так, как можно было бы ожидать, но если я попытайтесь отрисовать два треугольника друг над другом, ожидая, что тот, что ближе к камере, затемнит другой, это не всегда так. Похоже, что буфер A Z лучше всего подходит для решения этой проблемы, сохраняя значение z каждого пикселя, отображаемого на экране, и затем, если есть другой пиксель, пытающийся отобразиться с той же координатой, я сравниваю его со значением z текущего пикселя при решении, какой из них визуализировать. Проблема, с которой я сейчас сталкиваюсь, заключается в следующем:

Как определить значение z каждого пикселя, который я отображаю? Я думал об этом, и, кажется, есть несколько возможностей. Один из вариантов включает в себя нахождение уравнения плоскости (ax + by + cz + d = 0), на котором лежит грань, а затем некоторую интерполяцию каждого пикселя в отображаемом треугольнике (например, на полпути по оси x в двумерном отображаемом треугольнике). -> на полпути по оси x через 3-й треугольник, то же самое для y, затем решите для z, используя уравнение плоскости), хотя я не уверен, что это сработает. Другой вариант, о котором я подумал, - это перебирать каждую точку с заданным квантом трехмерного треугольника, а затем визуализировать каждую точку по отдельности, используя z этой точки (которую я, вероятно, также должен был бы найти через уравнение плоскости).

Опять же, в настоящее время я в основном рассматриваю возможность использования интерполяции, поэтому псевдокод будет выглядеть так (если бы у меня было уравнение плоскости как "ax + by + cz + d = 0"):

xrange = (pixel.x - 2dtriangle.minX)/(2dtriangle.maxX - 2dtriangle.minX)
yrange = (pixel.y - 2dtriangle.minY)/(2dtriangle.maxY - 2dtriangle.minY)
x3d = (3dtriangle.maxX - 3dtriangle.minX) * xrange + 3dtriangle.minX
y3d = (3dtriangle.maxY - 3dtriangle.minY) * yrange + 3dtriangel.minY
z = (-d - a*x3d - b*y3d)/c

куда pixel.x является значением х визуализируемого пикселя, 2dtraingle.minX а также 2dtriangle.maxX являются минимальными и максимальными значениями х представляемого треугольника (т.е. его ограничительной рамки) после проецирования на 2-мерный вид, и его минимальные / максимальные переменные Y такие же, но для его Y. 3dtriangle.minX а также 3dtriangle.maxX являются минимальными и максимальными значениями x трехмерного треугольника до того, как его спроецировали на 2d вид, a, b, c, and d являются коэффициентами уравнения плоскости, на которой лежит 3d треугольник, и z это соответствующее значение z визуализируемого пикселя.

Будет ли этот метод работать? Если есть двусмысленность, пожалуйста, дайте мне знать в комментариях, прежде чем закрывать вопрос! Спасибо.

Answer 1

Лучшим решением будет вычисление глубины для каждой вершины треугольника. Затем мы можем получить глубину каждого пикселя таким же образом, как мы делаем для цветов при рендеринге треугольника с затенением Гуро. Делая это одновременно с рендерингом, можно легко проверить глубину.

Если у нас такая ситуация:

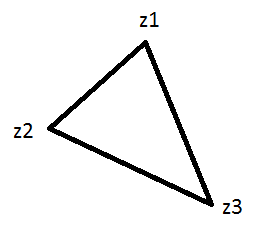
И мы начинаем рисовать линии сверху вниз. Мы рассчитываем наклоны от одной точки к остальным и добавляем правильное количество глубины каждый раз, когда переходим к следующей строке... И так далее.

Вы не предоставили свой метод рендеринга, поэтому не можете сказать что-то конкретное для него, но вы должны взглянуть на некоторые учебные пособия, касающиеся затенения Гуро. Сделайте несколько простых модификаций для них, и вы сможете использовать его со значениями глубины.

Ну, надеюсь, это поможет!