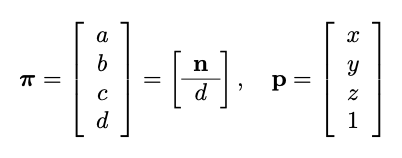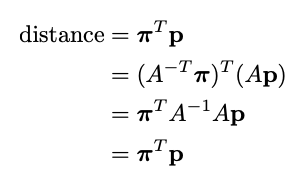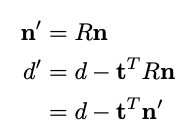Как эффективно вращать и переводить плоскость в 3D
У меня есть плоскость, определяемая нормалью (n) и расстоянием (d) (от начала координат). Я хотел бы превратить его в новую систему. Долгий путь таков: 1) умножить расстояние (d) на нормаль (n), в результате чего получается вектор (p) 2) повернуть (R) и перевести (v) вектор (p), чтобы получить (p') 3) нормализовать (p '), чтобы получить нормаль 4) использовать другой алгоритм, чтобы найти наименьшее расстояние (d') между новой плоскостью и началом координат
Я не пробовал это, но я думаю, это должно работать. ВОПРОС: Нет ли более быстрого способа получить n 'и d'? Если перевод (v) равен 0, то я могу пропустить 4). Но если это не 0? Есть ли более простой способ получить новый д '?
3 ответа
Вы должны быть осторожны, потому что нормали не обязательно преобразуются, как точки, а расстояние - это перпендикулярное расстояние до начала координат, поэтому вам нужно вычислить d'= d + n.v, Если все, что вы делаете, это перемещение и вращение, то вы можете повернуть нормаль и вычислить новое перпендикулярное расстояние. Но если вы по-разному масштабируете свои оси или делаете общее проективное преобразование, то вам нужно относиться к вещам по-другому.
Способ, который работает для всего, состоит в том, чтобы использовать однородные координаты, поэтому все ваши преобразования - это матрицы 4x4, а ваши точки и ваши плоскости - это 4-векторы:
point p=(x,y,z) -> homogeneous (x,y,z,1), equiv. to (x*W, y*W, z*W, W)
plane q=[n=(a,b,c), d] -> homogeneous [a,b,c,d], equiv. to [a*K, b*K, c*K, d*K)
-> point p is on plane q iff: p.q=0 (using homogeneous coords, as above)
Как правило, вы умножаете все свои матрицы преобразования в одну матрицу 4x4 T и используете эту матрицу в каждой точке, чтобы определить ее окончательное преобразованное положение. Хитрость в том, что вам нужно использовать обратную транспонированность T для преобразования координат вашей плоскости. Из следующего видно, что это сохраняет частоту между точками и плоскостями:
point p' = T p
plane q' = (T^-1)^t q
-> point p' is on plane q' when: p'.q'=0
then, note: p'.q' = p^t T^t (T^-1)^t q = p^t q = p.q
so: p'.q'=0 whenever p.q=0
Я собираюсь расширить ответы выше на случай, если люди захотят узнать еще несколько подробностей. Учитывая плоскость, определяемую ее нормалью n = [abc] ^ T и ее расстоянием d от начала координат (при условии, что n имеет величину 1) и однородной точкой p
Мы можем вычислить знаковое евклидово расстояние p от плоскости следующим образом
и обратите внимание , что если мы преобразуем p с помощью обратимого преобразования A , то расстояние от преобразованной точки сохраняется, если мы преобразуем плоскость обратным преобразованием A.
Для случая, когда A состоит из поворота R 3x3 и переноса t 3x1, мы имеем
Таким образом, у нас есть
Следовательно, новая нормаль и d' равны