JAGS - не удалось найти подходящий сэмплер
Я пытаюсь разработать иерархическую модель Дирихле-полиномиального процесса, скрытую по Маркову, в JAGS для оценки многопартийности, первичного намерения голосовать на основе результатов опроса. Я также использую первичную оценку голосов, чтобы вычислить предпочтительную долю голосов двух сторон в соответствии с системой избирательного голосования Австралии.
Полиномиальное распределение dmulti() завершилось ошибкой с сообщением об ошибке во время выполнения: не удалось найти подходящий сэмплер. У меня есть обходной путь, который использует серию биномиальных распределений и ограничение суммы в N. Теоретически, это должно дать тот же результат, но это создает неэффективность пространства и времени в модели.
Мой вопрос заключается в том, могу ли я что-то сделать в скрытой, временной части модели ниже, чтобы заставить работать многочленное распределение.
Модель (и окружающий код R) следующим образом:
data = list(PERIOD = PERIOD,
HOUSECOUNT = HOUSECOUNT,
NUMPOLLS = NUMPOLLS,
PARTIES = PARTIES,
primaryVotes = primaryVotes,
pollWeek = df$Week,
house = as.integer(df$House),
# manage rounding issues with df$Sample ...
n = rowSums(primaryVotes),
preference_flows = preference_flows
)
print(data)
# ----- JAGS model ...
library(rjags)
model <- "
model {
#### -- observational model
for(poll in 1:NUMPOLLS) { # for each poll result - rows
adjusted_poll[poll, 1:PARTIES] <- walk[pollWeek[poll], 1:PARTIES] +
houseEffect[house[poll], 1:PARTIES]
primaryVotes[poll, 1:PARTIES] ~ dmulti(adjusted_poll[poll, 1:PARTIES], n[poll])
}
#### -- temporal model (a weekly walk where this week is much like last week)
#tightness <- 30000 # KLUDGE: value selected by trial and error to look like DLM
t ~ dunif(1000, 100000) # less kludgy - let the model decide
tightness <- round(t)
for(week in 2:PERIOD) { # rows
# This results in a JAGS runtime error: Unable to find appropriate sampler
#multinomial[week, 1:PARTIES] ~ dmulti( walk[week-1, 1:PARTIES], tightness)
# This is the KLUDGE to approximate the above ...
# Should be the same theoretically ...
# but results in a larger directed acyclic graph (DAG)
for(party in 2:PARTIES) {
multinomial[week, party] ~ dbin(walk[week-1, party], tightness)
}
multinomial[week, 1] <- tightness - sum(multinomial[week, 2:PARTIES])
# The other part of the Dirichlet-Multinomial process
walk[week, 1:PARTIES] ~ ddirch(multinomial[week, 1:PARTIES])
}
## -- weakly informative priors for first week in the temporal model
for (party in 1:2) { # for each major party
alpha[party] ~ dunif(250, 600) # majors between 25% and 60%
}
for (party in 3:PARTIES) { # for each minor party
alpha[party] ~ dunif(10, 250) # minors between 1% and 25%
}
walk[1, 1:PARTIES] ~ ddirch(alpha[])
## -- estimate a Coalition TPP from the primary votes
for(week in 1:PERIOD) {
CoalitionTPP[week] <- sum(walk[week, 1:PARTIES] *
preference_flows[1:PARTIES])
}
#### -- sum-to-zero constraints on house effects
for (party in 2:PARTIES) { # for each party ...
# house effects across houses sum to zero
# NOTE: ALL MUST SUM TO ZERO
houseEffect[1, party] <- -sum( houseEffect[2:HOUSECOUNT, party] )
}
for(house in 1:HOUSECOUNT) { # for each house ...
# house effects across the parties sum to zero
houseEffect[house, 1] <- -sum( houseEffect[house, 2:PARTIES] )
}
# but note, we do not apply a double constraint to houseEffect[1, 1]
monitorHouseEffectOneSumParties <- sum(houseEffect[1, 1:PARTIES])
monitorHouseEffectOneSumHouses <- sum(houseEffect[1:HOUSECOUNT, 1])
## -- vague normal priors for house effects - centred on zero
for (party in 2:PARTIES) { # for each party (cols)
for(house in 2:HOUSECOUNT) { # (rows)
houseEffect[house, party] ~ dnorm(0, pow(0.1, -2))
}
}
}
"
jags <- jags.model(textConnection(model),
data = data,
n.chains=4,
n.adapt=n_adapt
)
Исходные данные для модели за шесть месяцев следующие.
$PERIOD
[1] 27
$HOUSECOUNT
[1] 5
$NUMPOLLS
[1] 37
$PARTIES
[1] 4
$primaryVotes
Coalition Labor Greens Other
[1,] 390 375 120 115
[2,] 407 407 143 143
[3,] 532 574 154 140
[4,] 560 518 168 154
[5,] 350 410 115 125
[6,] 439 450 139 127
[7,] 385 385 95 135
[8,] 375 395 120 110
[9,] 1465 1483 417 325
[10,] 504 602 154 140
[11,] 532 560 154 154
[12,] 504 602 154 140
[13,] 355 415 120 110
[14,] 412 483 141 141
[15,] 1345 1450 392 312
[16,] 375 405 100 120
[17,] 448 448 142 142
[18,] 588 504 168 140
[19,] 390 380 115 115
[20,] 441 453 139 128
[21,] 380 400 110 110
[22,] 471 425 126 126
[23,] 957 979 278 205
[24,] 405 360 125 110
[25,] 546 532 182 126
[26,] 471 413 126 138
[27,] 385 380 120 115
[28,] 1008 995 301 228
[29,] 400 375 115 110
[30,] 457 410 141 164
[31,] 690 656 185 151
[32,] 603 491 182 126
[33,] 415 355 125 105
[34,] 464 429 139 128
[35,] 1307 1218 385 273
[36,] 410 370 130 90
[37,] 479 433 152 105
$pollWeek
[1] 1 1 2 2 3 3 7 9 9 10 10 11 11 11 11 13 13 14 15 15 17 17 18 19 20
[26] 20 21 22 23 23 25 25 25 25 25 27 27
$house
[1] 3 4 1 2 3 4 3 3 5 1 2 1 3 4 5 3 4 2 3 4 3 4 5 3 2 4 3 5 3 4 1 2 3 4 5 3 4
$n
[1] 1000 1100 1400 1400 1000 1155 1000 1000 3690 1400 1400 1400 1000 1177 3499
[16] 1000 1180 1400 1000 1161 1000 1148 2419 1000 1386 1148 1000 2532 1000 1172
[31] 1682 1402 1000 1160 3183 1000 1169
$preference_flows
[1] 1.0000 0.0000 0.1697 0.5330
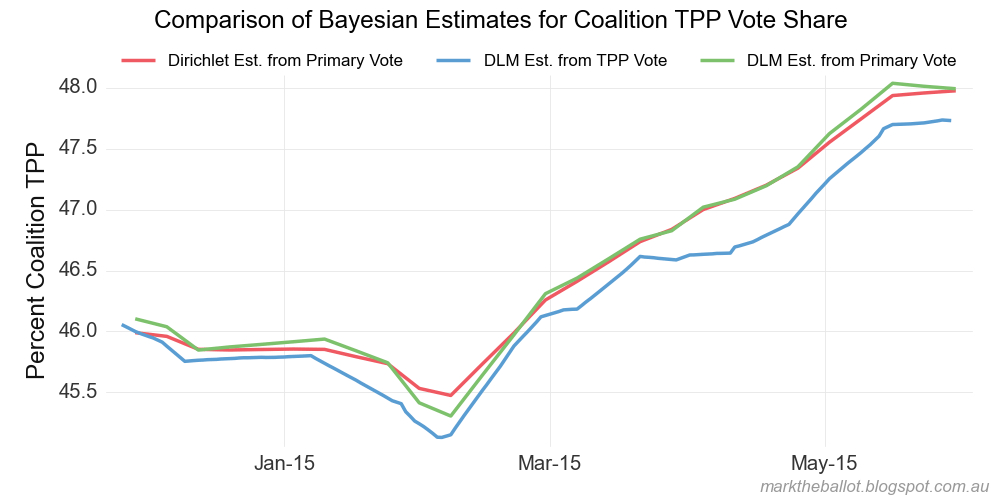
Сравнение результатов (по сравнению с другими моими моделями) следует. Красная линия на следующем графике была сгенерирована из приведенного выше.