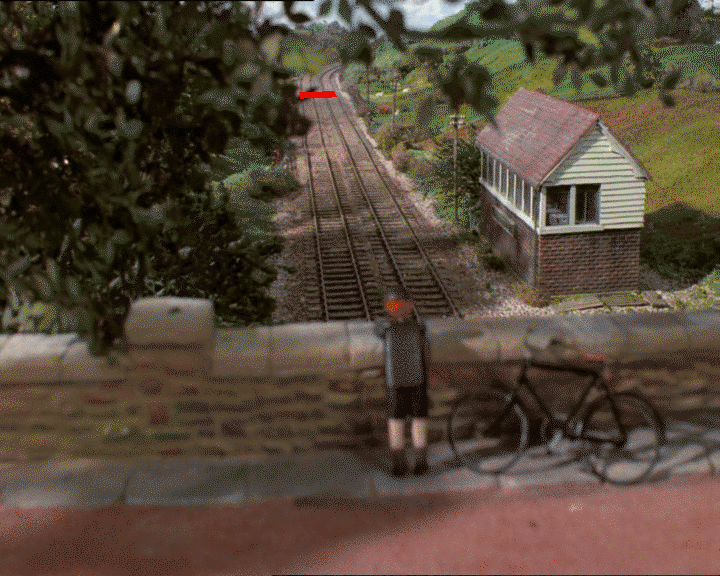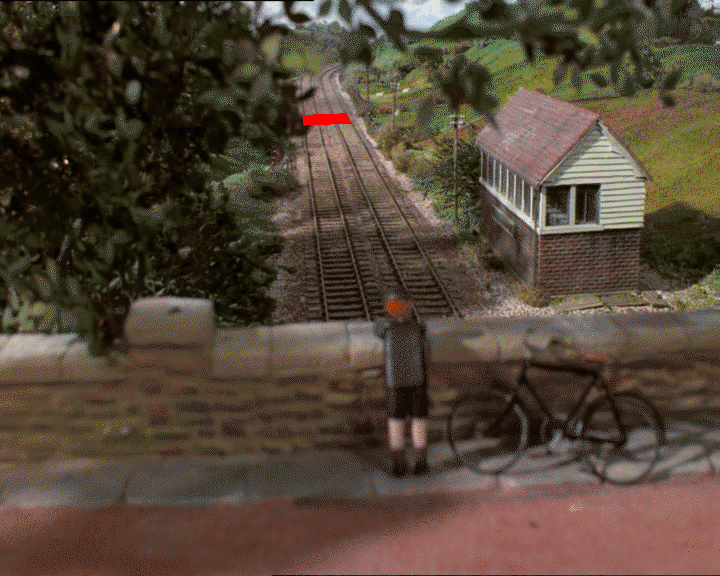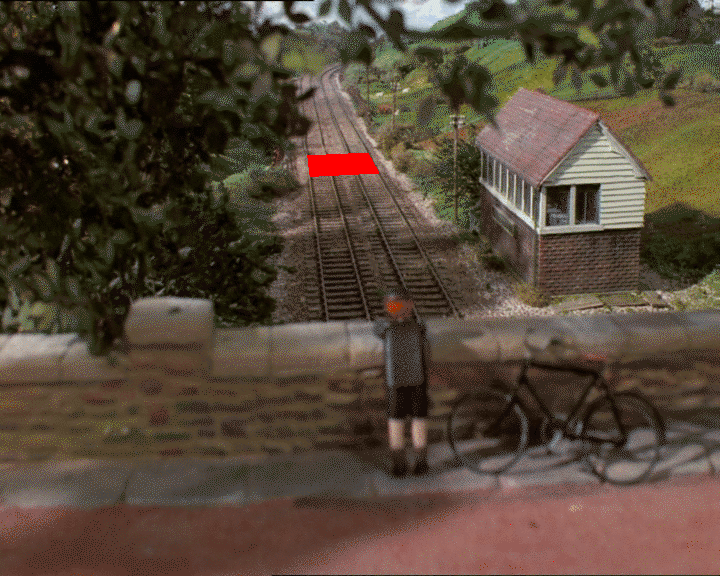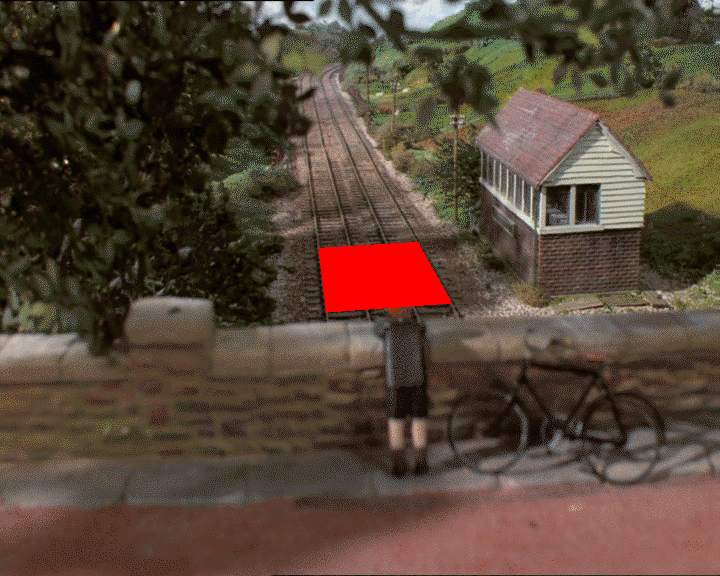Как я могу реверсировать 2D точки в 3D?
У меня есть 4 2D точки в экранном пространстве, и мне нужно перевести их обратно в 3D пространство. Я знаю, что каждая из 4 точек является углом жесткого прямоугольника, повернутого в 3D, и знаю размер прямоугольника. Как я могу получить 3D-координаты из этого?
Я не использую какой-либо конкретный API, и у меня нет существующей матрицы проекции. Я просто ищу основную математику, чтобы сделать это. Конечно, не хватает данных для преобразования одной 2D-точки в 3D без какой-либо другой ссылки, но я представляю, что если у вас есть 4 точки, вы знаете, что все они расположены под прямым углом друг к другу в одной плоскости, и вы знаете расстояние между ними, вы должны быть в состоянии выяснить это оттуда. К сожалению, я не могу понять, как, хотя.
Это может подпадать под эгиду фотограмметрии, но поиск в Google по этому поводу не привел меня к какой-либо полезной информации.
14 ответов
Хорошо, я пришел сюда в поисках ответа и не нашел ничего простого и понятного, поэтому я пошел дальше и сделал глупую, но эффективную (и относительно простую) вещь: оптимизацию Монте-Карло.
Проще говоря, алгоритм выглядит следующим образом: случайным образом возмущает матрицу проекции, пока она не проецирует ваши известные трехмерные координаты на ваши известные двухмерные координаты.
Вот еще фотография от двигателя танка Томаса:
Допустим, мы используем GIMP, чтобы найти 2D-координаты того, что мы считаем квадратом на плоскости земли (зависит от того, действительно ли это квадрат, зависит от вашего суждения о глубине):
Я получаю четыре очка на 2D-изображении: (318, 247), (326, 312), (418, 241), а также (452, 303),
Условно мы говорим, что эти точки должны соответствовать 3D точкам: (0, 0, 0), (0, 0, 1), (1, 0, 0), а также (1, 0, 1), Другими словами, единичный квадрат в плоскости y=0.
Проецирование каждой из этих трехмерных координат в 2D выполняется путем умножения 4D-вектора [x, y, z, 1] с матрицей проекции 4x4, затем разделив компоненты x и y на z, чтобы фактически получить коррекцию перспективы. Это более или менее то, что делает gluProject(), кроме gluProject() также учитывает текущий видовой экран и учитывает отдельную матрицу вида модели (мы можем просто предположить, что матрица вида модели - это единичная матрица). Это очень удобно смотреть на gluProject() документации, потому что я на самом деле хочу решение, которое работает для OpenGL, но учтите, что в документации отсутствует деление на z в формуле.
Помните, что алгоритм состоит в том, чтобы начать с некоторой матрицы проекций и беспорядочно возмущать ее, пока она не даст желаемую проекцию. Итак, что мы собираемся сделать, это спроектировать каждую из четырех трехмерных точек и посмотреть, насколько мы приблизились к желаемым 2D точкам. Если наши случайные возмущения приводят к тому, что проецируемые 2D-точки становятся ближе к тем, которые мы отметили выше, мы сохраняем эту матрицу как улучшение по сравнению с нашим первоначальным (или предыдущим) предположением.
Давайте определим наши точки:
# Known 2D coordinates of our rectangle
i0 = Point2(318, 247)
i1 = Point2(326, 312)
i2 = Point2(418, 241)
i3 = Point2(452, 303)
# 3D coordinates corresponding to i0, i1, i2, i3
r0 = Point3(0, 0, 0)
r1 = Point3(0, 0, 1)
r2 = Point3(1, 0, 0)
r3 = Point3(1, 0, 1)
Нам нужно начать с некоторой матрицы, тождественная матрица кажется естественным выбором:
mat = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
]
Нам нужно на самом деле реализовать проекцию (которая в основном является умножением матрицы):
def project(p, mat):
x = mat[0][0] * p.x + mat[0][1] * p.y + mat[0][2] * p.z + mat[0][3] * 1
y = mat[1][0] * p.x + mat[1][1] * p.y + mat[1][2] * p.z + mat[1][3] * 1
w = mat[3][0] * p.x + mat[3][1] * p.y + mat[3][2] * p.z + mat[3][3] * 1
return Point(720 * (x / w + 1) / 2., 576 - 576 * (y / w + 1) / 2.)
Это в основном то, что gluProject() действительно, 720 и 576 являются шириной и высотой изображения, соответственно (т. е. область просмотра), и мы вычитаем из 576, чтобы посчитать тот факт, что мы посчитали координаты y сверху, а OpenGL обычно считает их снизу. Вы заметите, что мы не вычисляем z, это потому, что нам это здесь не нужно (хотя это может быть удобно, чтобы убедиться, что оно попадает в диапазон, который OpenGL использует для буфера глубины).
Теперь нам нужна функция для оценки того, насколько мы близки к правильному решению. Значение, возвращаемое этой функцией - это то, что мы будем использовать, чтобы проверить, является ли одна матрица лучше другой. Я выбрал сумму квадратов расстояний, а именно:
# The squared distance between two points a and b
def norm2(a, b):
dx = b.x - a.x
dy = b.y - a.y
return dx * dx + dy * dy
def evaluate(mat):
c0 = project(r0, mat)
c1 = project(r1, mat)
c2 = project(r2, mat)
c3 = project(r3, mat)
return norm2(i0, c0) + norm2(i1, c1) + norm2(i2, c2) + norm2(i3, c3)
Чтобы возмущать матрицу, мы просто выбираем элемент для возмущения на случайную величину в некотором диапазоне:
def perturb(amount):
from copy import deepcopy
from random import randrange, uniform
mat2 = deepcopy(mat)
mat2[randrange(4)][randrange(4)] += uniform(-amount, amount)
(Стоит отметить, что наши project() функция на самом деле не использует mat[2] вообще, так как мы не вычисляем z, и так как все наши координаты y равны 0, mat[*][1] значения также не имеют значения. Мы могли бы использовать этот факт и никогда не пытаться нарушать те значения, которые могли бы привести к небольшому ускорению, но это оставлено в качестве упражнения...)
Для удобства добавим функцию, которая выполняет основную часть приближения, вызывая perturb() снова и снова на том, что является лучшей матрицей, которую мы нашли до сих пор:
def approximate(mat, amount, n=100000):
est = evaluate(mat)
for i in xrange(n):
mat2 = perturb(mat, amount)
est2 = evaluate(mat2)
if est2 < est:
mat = mat2
est = est2
return mat, est
Теперь все, что осталось сделать, это запустить его...:
for i in xrange(100):
mat = approximate(mat, 1)
mat = approximate(mat, .1)
Я считаю, что это уже дает довольно точный ответ. Через некоторое время я нашел следующую матрицу:
[
[1.0836000765696232, 0, 0.16272110011060575, -0.44811064935115597],
[0.09339193527789781, 1, -0.7990570384334473, 0.539087345090207 ],
[0, 0, 1, 0 ],
[0.06700844759602216, 0, -0.8333379578853196, 3.875290562060915 ],
]
с ошибкой около 2.6e-5, (Обратите внимание, что элементы, которые мы сказали, не использовались в вычислениях, на самом деле не были изменены по сравнению с нашей исходной матрицей; это потому, что изменение этих записей не приведет к изменению результата оценки, и поэтому изменение никогда не будет выполнено.)
Мы можем передать матрицу в OpenGL, используя glLoadMatrix() (но не забудьте сначала перенести его, и не забудьте загрузить матрицу вида модели с матрицей идентичности):
def transpose(m):
return [
[m[0][0], m[1][0], m[2][0], m[3][0]],
[m[0][1], m[1][1], m[2][1], m[3][1]],
[m[0][2], m[1][2], m[2][2], m[3][2]],
[m[0][3], m[1][3], m[2][3], m[3][3]],
]
glLoadMatrixf(transpose(mat))
Теперь мы можем, например, переместить по оси Z, чтобы получить разные позиции вдоль дорожек:
glTranslate(0, 0, frame)
frame = frame + 1
glBegin(GL_QUADS)
glVertex3f(0, 0, 0)
glVertex3f(0, 0, 1)
glVertex3f(1, 0, 1)
glVertex3f(1, 0, 0)
glEnd()
Конечно, это не очень элегантно с математической точки зрения; вы не получите уравнение в замкнутой форме, в которое вы можете просто вставить свои числа и получить прямой (и точный) ответ. ОДНАКО, это позволяет вам добавлять дополнительные ограничения, не беспокоясь о усложнении ваших уравнений; например, если мы хотим также указать высоту, мы могли бы использовать этот угол дома и сказать (в нашей функции оценки), что расстояние от земли до крыши должно быть примерно одинаковым, и снова запустить алгоритм. Так что да, это своего рода грубая сила, но она работает и работает хорошо.
Это классическая проблема для маркеров на основе дополненной реальности.
У вас есть квадратный маркер (2D штрих-код), и вы хотите найти его позу (перемещение и вращение относительно камеры) после нахождения четырех краев маркера. Обзор-Picture
Я не в курсе последних вкладов в эту область, но, по крайней мере, до определенного момента (2009 г.) RPP должен был превзойти ПОЗИТ, который упомянут выше (и это действительно классический подход для этого). Пожалуйста, смотрите ссылки, они также предоставить источник.
http://www.emt.tugraz.at/publications/EMT_TR/TR-EMT-2005-01.pdf
http://www.emt.tugraz.at/system/files/rpp_MATLAB_ref_implementation.tar.gz
(PS - я знаю, что это немного старая тема, но в любом случае, пост может быть полезен для кого-то)
Д. Дементон разработал алгоритм для вычисления позы объекта (его положения и ориентации в пространстве) по характерным точкам на двухмерном изображении при знании модели объекта - это ваша точная проблема:
Опишем метод нахождения позы объекта по одному изображению. Мы предполагаем, что мы можем обнаружить и сопоставить на изображении четыре или более некомпланарных характерных точки объекта и что мы знаем их относительную геометрию на объекте.
Алгоритм известен как Posit и описан в классической статье "Поза объекта на основе модели в 25 строках кода" (доступна на его веб-сайте, раздел 4).
Прямая ссылка на статью: http://www.cfar.umd.edu/~daniel/daniel_papersfordownload/Pose25 Lines.pdf Реализация OpenCV: http://opencv.willowgarage.com/wiki/Posit
Идея состоит в том, чтобы многократно аппроксимировать перспективную проекцию масштабированной ортографической проекцией, пока не сойдется в точную позу.
Для моего движка OpenGL следующий фрагмент преобразует координаты мыши / экрана в трехмерные мировые координаты. Прочитайте комментарии для фактического описания того, что происходит.
/ * ФУНКЦИЯ: YCamera:: CalculateWorldCoordinates
АРГУМЕНТЫ: х мышь х координата
y мышь y координата
vec где хранить координаты
ВОЗВРАТ: н / п
ОПИСАНИЕ: конвертировать координаты мыши в мировые координаты
* /
void YCamera :: CalculateWorldCoordinates(float x, float y, YVector3 *vec)
{
// START
GLint viewport[4];
GLdouble mvmatrix[16], projmatrix[16];
GLint real_y; GLdouble mx, my, mz; glGetIntegerv(GL_VIEWPORT, viewport); glGetDoublev(GL_MODELVIEW_MATRIX, mvmatrix); glGetDoublev(GL_PROJECTION_MATRIX, projmatrix); real_y = viewport[3] - (GLint) y - 1; // viewport[3] is height of window in pixels gluUnProject((GLdouble) x, (GLdouble) real_y, 1.0, mvmatrix, projmatrix, viewport, &mx, &my, &mz); /* 'mouse' is the point where mouse projection reaches FAR_PLANE. World coordinates is intersection of line(camera->mouse) with plane(z=0) (see LaMothe 306) Equation of line in 3D: (x-x0)/a = (y-y0)/b = (z-z0)/c Intersection of line with plane: z = 0 x-x0 = a(z-z0)/c <=> x = x0+a(0-z0)/c <=> x = x0 -a*z0/c y = y0 - b*z0/c */ double lx = fPosition.x - mx; double ly = fPosition.y - my; double lz = fPosition.z - mz; double sum = lx*lx + ly*ly + lz*lz; double normal = sqrt(sum); double z0_c = fPosition.z / (lz/normal); vec->x = (float) (fPosition.x - (lx/normal)*z0_c); vec->y = (float) (fPosition.y - (ly/normal)*z0_c); vec->z = 0.0f;}
Из двумерного пространства будет 2 допустимых прямоугольника, которые можно построить. Не зная исходную матричную проекцию, вы не узнаете, какая из них правильная. Это то же самое, что и проблема "коробки": вы видите два квадрата, один внутри другого, с 4 внутренними вершинами, соединенными с 4 соответствующими внешними вершинами. Вы смотрите на коробку сверху вниз или снизу вверх?
При этом вы ищете матричное преобразование T, где...
{{x1, y1, z1}, {x2, y2, z2}, {x3, y3, z3}, {x4, y4, z4}} x T = {{x1, y1}, {x2, y2}, { x3, y3}, {x4, y4}}
(4 х 3) х Т = (4 х 2)
Таким образом, T должна быть (3 x 2) матрица. Итак, у нас есть 6 неизвестных.
Теперь создайте систему ограничений на T и решите ее с помощью Simplex. Чтобы построить ограничения, вы знаете, что линия, проходящая через первые две точки, должна быть параллельна линии, проходящей ко вторым двум точкам. Вы знаете, что линия, проходящая через точки 1 и 3, должна быть параллельной линиям, проходящим через точки 2 и 4. Вы знаете, что линия, проходящая через точки 1 и 2, должна быть ортогональной линии, проходящей через точки 2 и 3. Вы знаете, что длина линии от 1 и 2 должны равняться длине строки от 3 и 4. Вы знаете, что длина строки от 1 и 3 должна равняться длине строки от 2 и 4.
Чтобы сделать это еще проще, вы знаете о прямоугольнике, поэтому вы знаете длину всех сторон.
Это должно дать вам множество ограничений для решения этой проблемы.
Конечно, чтобы вернуться, вы можете найти T-Inverse.
@Rob: Да, существует бесконечное количество проекций, но не бесконечное количество проектов, где точки должны удовлетворять требованиям прямоугольника.
@nlucaroni: Да, это решаемо, только если у вас есть четыре точки в проекции. Если прямоугольник проецируется только на 2 точки (т.е. плоскость прямоугольника ортогональна поверхности проекции), то это не может быть решено.
Хммм... я должен пойти домой и написать этот маленький драгоценный камень. Это звучит как веселье.
Обновления:
- Существует бесконечное количество проекций, если вы не исправите один из пунктов. Если вы зафиксируете одну из точек исходного прямоугольника, то есть два возможных исходных прямоугольника.
Для продолжения подхода Ронса: Вы можете найти свои z-значения, если знаете, как вы повернули прямоугольник.
Хитрость заключается в том, чтобы найти проективную матрицу, которая сделала проекцию. К счастью, это возможно и даже дешево. Соответствующая математика может быть найдена в статье Пола Хекберта "Проективные отображения для деформации изображения".
http://pages.cs.wisc.edu/~dyer/cs766/readings/heckbert-proj.pdf
Таким образом, вы можете восстановить однородную часть каждой вершины назад, которая была потеряна во время проецирования.
Теперь у вас остались четыре линии вместо точек (как объяснил Рон). Так как вы знаете размер вашего оригинального прямоугольника, ничего не потеряно. Теперь вы можете подключить данные из метода Рона и из двумерного подхода в решатель линейных уравнений и решить для z. Таким образом вы получите точные значения z каждой вершины.
Примечание. Это работает только потому, что:
- Первоначальная форма была прямоугольником
- Вы знаете точный размер прямоугольника в трехмерном пространстве.
Это действительно особый случай.
Надеюсь, это поможет, Нильс
Предполагая, что точки действительно являются частью прямоугольника, я даю общую идею:
Найдите две точки с максимальным расстоянием между ними: они, скорее всего, определяют диагональ (исключение: особые случаи, когда прямоугольник почти параллелен плоскости YZ, оставленный для студента). Назовите их A, C. Рассчитайте BAD, BCD углы. Они, по сравнению с прямыми углами, дают вам ориентацию в трехмерном пространстве. Чтобы узнать расстояние z, необходимо сопоставить проекционные стороны с известными сторонами, а затем, основываясь на методе трехмерного проецирования (это 1/z?), Вы на правильном пути, чтобы узнать расстояния.
Спасибо @Vegard за отличный ответ. Я немного очистил код:
import pandas as pd
import numpy as np
class Point2:
def __init__(self,x,y):
self.x = x
self.y = y
class Point3:
def __init__(self,x,y,z):
self.x = x
self.y = y
self.z = z
# Known 2D coordinates of our rectangle
i0 = Point2(318, 247)
i1 = Point2(326, 312)
i2 = Point2(418, 241)
i3 = Point2(452, 303)
# 3D coordinates corresponding to i0, i1, i2, i3
r0 = Point3(0, 0, 0)
r1 = Point3(0, 0, 1)
r2 = Point3(1, 0, 0)
r3 = Point3(1, 0, 1)
mat = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
]
def project(p, mat):
#print mat
x = mat[0][0] * p.x + mat[0][1] * p.y + mat[0][2] * p.z + mat[0][3] * 1
y = mat[1][0] * p.x + mat[1][1] * p.y + mat[1][2] * p.z + mat[1][3] * 1
w = mat[3][0] * p.x + mat[3][1] * p.y + mat[3][2] * p.z + mat[3][3] * 1
return Point2(720 * (x / w + 1) / 2., 576 - 576 * (y / w + 1) / 2.)
# The squared distance between two points a and b
def norm2(a, b):
dx = b.x - a.x
dy = b.y - a.y
return dx * dx + dy * dy
def evaluate(mat):
c0 = project(r0, mat)
c1 = project(r1, mat)
c2 = project(r2, mat)
c3 = project(r3, mat)
return norm2(i0, c0) + norm2(i1, c1) + norm2(i2, c2) + norm2(i3, c3)
def perturb(mat, amount):
from copy import deepcopy
from random import randrange, uniform
mat2 = deepcopy(mat)
mat2[randrange(4)][randrange(4)] += uniform(-amount, amount)
return mat2
def approximate(mat, amount, n=1000):
est = evaluate(mat)
for i in xrange(n):
mat2 = perturb(mat, amount)
est2 = evaluate(mat2)
if est2 < est:
mat = mat2
est = est2
return mat, est
for i in xrange(1000):
mat,est = approximate(mat, 1)
print mat
print est
Примерный звонок с.1 у меня не сработал, поэтому я его вынул. Я тоже запускал его некоторое время, и последний раз проверял, что это
[[0.7576315397559887, 0, 0.11439449272592839, -0.314856490473439],
[0.06440497208710227, 1, -0.5607502645413118, 0.38338196981556827],
[0, 0, 1, 0],
[0.05421620936883742, 0, -0.5673977598434641, 2.693116299312736]]
с ошибкой около 0,02.
Если вы знаете, что фигура представляет собой прямоугольник на плоскости, вы можете значительно ограничить проблему. Вы, конечно, не можете определить, "какая" плоскость, поэтому вы можете выбрать, чтобы она лежала на плоскости, где z=0, а один из углов находится в точке x=y=0, а ребра параллельны оси x/y.
Следовательно, точки в 3d - это {0,0,0},{w,0,0},{w,h,0} и {0,h,0}. Я почти уверен, что абсолютный размер не будет найден, поэтому только соотношение w/h является релевантным, так что это неизвестно.
Относительно этой плоскости камера должна находиться в некоторой точке cx,cy,cz в пространстве, должна указывать в направлении nx,ny,nz (вектор длины один, поэтому один из них является избыточным) и иметь focal_length/image_width фактор ш. Эти числа превращаются в матрицу проекции 3х3.
Это дает в общей сложности 7 неизвестных: w/h, cx, cy, cz, nx, ny и w.
Всего известно 8 пар: 4 пары x+y.
Так что это можно решить.
Следующим шагом является использование Matlab или Mathmatica.
Когда вы проецируете из 3D в 2D, вы теряете информацию.
В простом случае одной точки обратная проекция даст вам бесконечный луч через трехмерное пространство.
Стереоскопическая реконструкция обычно начинается с двух 2D-изображений и проецируется обратно в 3D. Затем найдите пересечение двух трехмерных лучей.
Проекция может принимать разные формы. Ортогональный или перспективный. Я предполагаю, что вы предполагаете ортогональную проекцию?
В вашем случае, предполагая, что у вас была исходная матрица, у вас будет 4 луча в трехмерном пространстве. После этого вы сможете ограничить проблему своими размерами в 3D-прямоугольнике и попытаться ее решить.
Решение не будет уникальным, поскольку вращение вокруг любой оси, параллельной 2-й плоскости проекции, будет неоднозначным в направлении. Другими словами, если двумерное изображение перпендикулярно оси z, то вращение трехмерного прямоугольника по часовой стрелке или против часовой стрелки вокруг оси x приведет к тому же изображению. Аналогично для оси у.
В случае, когда плоскость прямоугольника параллельна оси z, у вас есть еще больше решений.
Поскольку у вас нет исходной матрицы проекций, дальнейшая неоднозначность вносится произвольным масштабным коэффициентом, который существует в любой проекции. Вы не можете различить масштабирование в проекции и перевод в 3d в направлении оси z. Это не проблема, если вас интересуют только относительные положения 4-х точек в трехмерном пространстве, когда они связаны друг с другом, а не с плоскостью 2-мерной проекции.
В перспективе все становится сложнее...
Я достану свою книгу по линейной алгебре, когда вернусь домой, если никто не ответит. Но @ D G, не все матрицы обратимы. Сингулярные матрицы необратимы (когда определитель = 0). На самом деле это будет происходить все время, поскольку матрица проекции должна иметь собственные значения 0 и 1 и быть квадратной (поскольку она идемпотентна, поэтому p^2 = p).
Простой пример: [[0 1][0 1]], так как определитель = 0, и это проекция на линию x = y!
Да, Монте-Карло работает, но я нашел лучшее решение для этой проблемы. Этот код отлично работает (и использует OpenCV):
Cv2.CalibrateCamera(new List<List<Point3f>>() { points3d }, new List<List<Point2f>>() { points2d }, new Size(height, width), cameraMatrix, distCoefs, out rvecs, out tvecs, CalibrationFlags.ZeroTangentDist | CalibrationFlags.FixK1 | CalibrationFlags.FixK2 | CalibrationFlags.FixK3);
Эта функция принимает известные 3d и 2d точки, размер экрана и возвращает вращение (rvecs[0]), перевод (tvecs[0]) и матрицу внутренних значений камеры. Это все, что вам нужно.
Проекция, которую вы имеете на 2D-поверхность, имеет бесконечно много 3D-прямоугольников, которые будут проецироваться на одну и ту же 2D-форму.
Подумайте об этом так: у вас есть четыре 3D-точки, которые составляют 3D-прямоугольник. Назовите их (x0,y0,z0), (x1,y1,z1), (x2,y2,z2) и (x3,y3,z3). Когда вы проецируете эти точки на плоскость xy, вы отбрасываете координаты z: (x0,y0), (x1,y1), (x2,y2), (x3,y3).
Теперь, если вы хотите спроецировать обратно в трехмерное пространство, вам нужно перепроектировать то, чем были z0,..,z3. Но любой набор координат z, которые а) сохраняют одинаковое расстояние ху между точками, и б) сохраняют форму прямоугольника, будут работать. Таким образом, любой член этого (бесконечного) множества будет делать: {(z0+i, z1+i, z2+i, z3+i) | я <- R}.
Edit @Jarrett: представьте, что вы решили это и получили прямоугольник в трехмерном пространстве. Теперь представьте, что вы двигаете этот прямоугольник вверх и вниз по оси Z. Те бесконечные количества переведенных прямоугольников имеют одинаковую проекцию xy. Откуда ты знаешь, что нашел "правильный"?
Edit # 2: Хорошо, это из комментария, который я сделал по этому вопросу - более интуитивный подход к рассуждению об этом.
Представьте себе, что вы держите лист бумаги над столом. Представьте, что к каждому углу бумаги прикреплена невесомая лазерная указка, которая указывает вниз на стол. Бумага - это 3D-объект, а точки лазерной указки на столе - это 2D-проекция.
Теперь, как вы можете определить, насколько высоко находится стол, глядя на точки лазерного указателя?
Ты не можешь Переместите бумагу прямо вверх и вниз. Лазерные указки по-прежнему будут светиться в тех же точках на столе, независимо от высоты бумаги.
Нахождение z-координат в обратной проекции - это все равно, что пытаться найти высоту бумаги на основе точек лазерного указателя только на столе.
http://library.wolfram.com/infocenter/Articles/2794/
http://campar.in.tum.de/Students/SepPoseEstimation
http://opencvlibrary.sourceforge.net/Posit будет работать, но он может расходиться или зацикливаться.