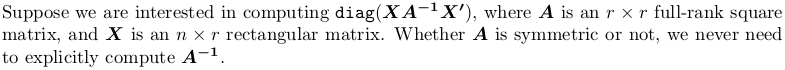Как эффективно вычислить diag(X %*% solve(A) %*% t(X)) без обратной матрицы?

Мне нужна следующая диагональ:

diag(X %*% solve(A) %*% t(X))

где A квадратная матрица полного ранга, X прямоугольная матрица И то и другое A а также X редки

Я знаю, что найти обратную матрицу плохо, если она тебе действительно не нужна. Однако я не вижу, как переписать формулу так, чтобы solve(A) заменяется solve с двумя аргументами, такими, что линейная система решается без явного обращения. Это возможно?

Источник

1 ответ

Решение

Возможно, прежде чем я действительно начну, я должен упомянуть, что если вы делаете

diag(X %*% solve(A, t(X)))

обратная матрица исключается. solve(A, B) выполняет факторизацию LU и использует полученные треугольные матричные коэффициенты для решения линейной системы A x = B, Если ты уйдешь B не указано, по умолчанию это диагональная матрица, следовательно, вы будете явно вычислять матрицу, обратную A,

Вы должны прочитать ?solve осторожно, и, возможно, много раз для подсказок. Он говорит, что основан на LAPACK рутинный DGESV где вы можете найти числовую линейную алгебру за сценой.

DGESV computes the solution to a real system of linear equations

   A * X = B,

where A is an N-by-N matrix and X and B are N-by-N RHS matrices.

The LU decomposition with partial pivoting and row interchanges is
used to factor A as

  A = P * L * U,

where P is a permutation matrix, L is unit lower triangular, and U is
upper triangular.  The factored form of A is then used to solve the
system of equations A * X = B.

Разница между solve(A, t(X)) а также solve(A) %*% t(X) это вопрос эффективности. Общая матрица умножения %*% в последнем намного дороже чем solve сам.

Тем не менее, даже если вы используете solve(A, t(X)), вы не на самой быстрой трассе, так как у вас есть другой %*%,

Кроме того, поскольку вам нужны только диагональные элементы, вы сначала тратите значительное время на получение полной матрицы. Мой ответ ниже даст вам быстрый путь.

Я переписал все в LaTeX, и его содержание также значительно расширилось, включая ссылку на реализацию R. Дополнительные ресурсы предоставляются на факторизацию QR, разложение по сингулярным значениям и факторизацию Pivoted-Cholesky в конце, если вы считаете их полезными.

обзор

Чхоль

лу

Дополнительные ресурсы

В случае, если вас интересует сводная факторизация Холецкого, вы можете обратиться к матрице Compute projection / hat через QR-факторизацию, SVD (и факторизацию Холецкого?). Там я также обсуждаю QR факторизацию и разложение по сингулярным числам.

Приведенная выше ссылка устанавливается в обычном контексте наименьших квадратов. Для взвешенного наименьшего квадрата вы можете обратиться к матрице Получить шляпу из разложения QR для взвешенной регрессии наименьших квадратов.

QR-факторизация также принимает компактную форму. Если вы хотите узнать больше о том, как выполняется и хранится QR-факторизация, вы можете обратиться к разделу "Что такое"qraux", возвращаемое декомпозицией QR-кода?

Все эти вопросы и ответы сосредоточены на численных матричных вычислениях. Следующее дает некоторое статистическое применение:

Источник
Другие вопросы по тегам