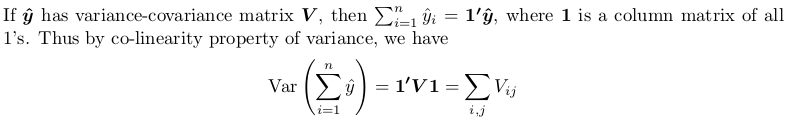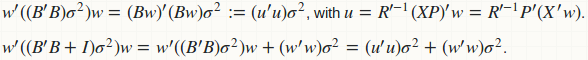Линейная модель с `lm`: как получить прогнозную дисперсию суммы прогнозируемых значений
Я суммирую предсказанные значения из линейной модели с несколькими предикторами, как в примере ниже, и хочу вычислить объединенную дисперсию, стандартную ошибку и, возможно, доверительные интервалы для этой суммы.
lm.tree <- lm(Volume ~ poly(Girth,2), data = trees)
Предположим, у меня есть набор Girths:
newdat <- list(Girth = c(10,12,14,16)
для которого я хочу предсказать общее Volume:
pr <- predict(lm.tree, newdat, se.fit = TRUE)
total <- sum(pr$fit)
# [1] 111.512
Как я могу получить дисперсию для total?
Подобные вопросы здесь (для GAM), но я не уверен, как поступить с vcov(lm.trees), Я был бы благодарен за ссылку на метод.
1 ответ
Вам необходимо получить полную дисперсионно-ковариационную матрицу, а затем суммировать все ее элементы. Вот небольшое доказательство:
Доказательством здесь является использование другой теоремы, которую вы можете найти в Covariance-wikipedia:
В частности, линейное преобразование, которое мы берем, представляет собой матрицу столбцов всех единиц. Результирующая квадратичная форма вычисляется следующим образом, со всеми x_i а также x_j быть 1.
Настроить
## your model
lm.tree <- lm(Volume ~ poly(Girth, 2), data = trees)
## newdata (a data frame)
newdat <- data.frame(Girth = c(10, 12, 14, 16))
Повторно реализовать predict.lm вычислить дисперсионно-ковариационную матрицу
См. Как Forex.lm() вычисляет доверительный интервал и интервал прогнозирования? на сколько predict.lm работает. Следующая маленькая функция lm_predict имитирует то, что он делает, за исключением того, что
- он не строит доверительный интервал или интервал прогнозирования (но построение очень простое, как объяснено в этом Q & A);
- он может вычислить полную дисперсионно-ковариационную матрицу предсказанных значений, если
diag = FALSE; - возвращает дисперсию (как для прогнозируемых значений, так и для остатков), а не стандартную ошибку;
- это не может сделать
type = "terms"; это только предсказывает переменную ответа.
lm_predict <- function (lmObject, newdata, diag = TRUE) {
## input checking
if (!inherits(lmObject, "lm")) stop("'lmObject' is not a valid 'lm' object!")
## extract "terms" object from the fitted model, but delete response variable
tm <- delete.response(terms(lmObject))
## linear predictor matrix
Xp <- model.matrix(tm, newdata)
## predicted values by direct matrix-vector multiplication
pred <- c(Xp %*% coef(lmObject))
## efficiently form the complete variance-covariance matrix
QR <- lmObject$qr ## qr object of fitted model
piv <- QR$pivot ## pivoting index
r <- QR$rank ## model rank / numeric rank
if (is.unsorted(piv)) {
## pivoting has been done
B <- forwardsolve(t(QR$qr), t(Xp[, piv]), r)
} else {
## no pivoting is done
B <- forwardsolve(t(QR$qr), t(Xp), r)
}
## residual variance
sig2 <- c(crossprod(residuals(lmObject))) / df.residual(lmObject)
if (diag) {
## return point-wise prediction variance
VCOV <- colSums(B ^ 2) * sig2
} else {
## return full variance-covariance matrix of predicted values
VCOV <- crossprod(B) * sig2
}
list(fit = pred, var.fit = VCOV, df = lmObject$df.residual, residual.var = sig2)
}
Мы можем сравнить его результат с predict.lm:
predict.lm(lm.tree, newdat, se.fit = TRUE)
#$fit
# 1 2 3 4
#15.31863 22.33400 31.38568 42.47365
#
#$se.fit
# 1 2 3 4
#0.9435197 0.7327569 0.8550646 0.8852284
#
#$df
#[1] 28
#
#$residual.scale
#[1] 3.334785
lm_predict(lm.tree, newdat)
#$fit
#[1] 15.31863 22.33400 31.38568 42.47365
#
#$var.fit ## the square of `se.fit`
#[1] 0.8902294 0.5369327 0.7311355 0.7836294
#
#$df
#[1] 28
#
#$residual.var ## the square of `residual.scale`
#[1] 11.12079
И в частности:
oo <- lm_predict(lm.tree, newdat, FALSE)
oo
#$fit
#[1] 15.31863 22.33400 31.38568 42.47365
#
#$var.fit
# [,1] [,2] [,3] [,4]
#[1,] 0.89022938 0.3846809 0.04967582 -0.1147858
#[2,] 0.38468089 0.5369327 0.52828797 0.3587467
#[3,] 0.04967582 0.5282880 0.73113553 0.6582185
#[4,] -0.11478583 0.3587467 0.65821848 0.7836294
#
#$df
#[1] 28
#
#$residual.var
#[1] 11.12079
Обратите внимание, что матрица дисперсии-ковариации не вычисляется наивным способом: Xp %*% vcov(lmObject) % t(Xp), что медленно.
Агрегация (сумма)
В вашем случае операция агрегирования является суммой всех значений в oo$fit, Среднее значение и дисперсия этой агрегации
sum_mean <- sum(oo$fit) ## mean of the sum
# 111.512
sum_variance <- sum(oo$var.fit) ## variance of the sum
# 6.671575
Далее вы можете построить доверительный интервал (CI) для этого агрегированного значения, используя t-распределение и остаточную степень свободы в модели.
alpha <- 0.95
Qt <- c(-1, 1) * qt((1 - alpha) / 2, lm.tree$df.residual, lower.tail = FALSE)
#[1] -2.048407 2.048407
## %95 CI
sum_mean + Qt * sqrt(sum_variance)
#[1] 106.2210 116.8029
Построение интервала прогнозирования (PI) требует дальнейшего учета остаточной дисперсии.
## adjusted variance-covariance matrix
VCOV_adj <- with(oo, var.fit + diag(residual.var, nrow(var.fit)))
## adjusted variance for the aggregation
sum_variance_adj <- sum(VCOV_adj) ## adjusted variance of the sum
## 95% PI
sum_mean + Qt * sqrt(sum_variance_adj)
#[1] 96.86122 126.16268
Агрегация (в целом)
Общая операция агрегации может быть линейной комбинацией oo$fit:
w[1] * fit[1] + w[2] * fit[2] + w[3] * fit[3] + ...
Например, операция суммирования имеет все веса, равные 1; средняя операция имеет все веса, равные 0,25 (в случае 4 данных). Вот функция, которая принимает весовой вектор, уровень значимости и что возвращается lm_predict производить статистику агрегации.
agg_pred <- function (w, predObject, alpha = 0.95) {
## input checing
if (length(w) != length(predObject$fit)) stop("'w' has wrong length!")
if (!is.matrix(predObject$var.fit)) stop("'predObject' has no variance-covariance matrix!")
## mean of the aggregation
agg_mean <- c(crossprod(predObject$fit, w))
## variance of the aggregation
agg_variance <- c(crossprod(w, predObject$var.fit %*% w))
## adjusted variance-covariance matrix
VCOV_adj <- with(predObject, var.fit + diag(residual.var, nrow(var.fit)))
## adjusted variance of the aggregation
agg_variance_adj <- c(crossprod(w, VCOV_adj %*% w))
## t-distribution quantiles
Qt <- c(-1, 1) * qt((1 - alpha) / 2, predObject$df, lower.tail = FALSE)
## names of CI and PI
NAME <- c("lower", "upper")
## CI
CI <- setNames(agg_mean + Qt * sqrt(agg_variance), NAME)
## PI
PI <- setNames(agg_mean + Qt * sqrt(agg_variance_adj), NAME)
## return
list(mean = agg_mean, var = agg_variance, CI = CI, PI = PI)
}
Быстрый тест на предыдущую операцию суммы:
agg_pred(rep(1, length(oo$fit)), oo)
#$mean
#[1] 111.512
#
#$var
#[1] 6.671575
#
#$CI
# lower upper
#106.2210 116.8029
#
#$PI
# lower upper
# 96.86122 126.16268
И быстрый тест для средней работы:
agg_pred(rep(1, length(oo$fit)) / length(oo$fit), oo)
#$mean
#[1] 27.87799
#
#$var
#[1] 0.4169734
#
#$CI
# lower upper
#26.55526 29.20072
#
#$PI
# lower upper
#24.21531 31.54067
замечание
Этот ответ улучшен, чтобы обеспечить простые в использовании функции для линейной регрессии с помощью `lm()`: интервал прогнозирования для агрегированных прогнозных значений.
Обновление (для больших данных)
Это замечательно! Спасибо вам большое! Я забыл упомянуть одну вещь: в моем реальном приложении мне нужно суммировать ~300000 прогнозов, которые создали бы полную дисперсионно-ковариационную матрицу размером около ~700 ГБ. Есть ли у вас какие-либо идеи, если существует более эффективный в вычислительном отношении способ прямого получения суммы дисперсионно-ковариационной матрицы?
Благодаря OP линейной регрессии с `lm()`: интервал прогнозирования для агрегированных прогнозных значений для этого очень полезного комментария. Да, это возможно, и это (значительно) в вычислительном отношении дешевле. В данный момент, lm_predict сформировать дисперсию-ковариацию как таковую:
agg_pred вычисляет дисперсию прогноза (для построения КИ) в виде квадратичной формы: w'(B'B)wи прогнозирование дисперсии (для построения PI) в качестве другой квадратичной формы w'(B'B + D)w, где D является диагональной матрицей остаточной дисперсии. Очевидно, что если мы объединим эти две функции, у нас будет лучшая вычислительная стратегия:
Вычисление B а также B'B избегается; мы заменили все умножение матрицы на матрицу умножением матрицы на вектор. Нет памяти для хранения B а также B'B; только для u который просто вектор. Вот слитная реализация.
## this function requires neither `lm_predict` nor `agg_pred`
fast_agg_pred <- function (w, lmObject, newdata, alpha = 0.95) {
## input checking
if (!inherits(lmObject, "lm")) stop("'lmObject' is not a valid 'lm' object!")
if (!is.data.frame(newdata)) newdata <- as.data.frame(newdata)
if (length(w) != nrow(newdata)) stop("length(w) does not match nrow(newdata)")
## extract "terms" object from the fitted model, but delete response variable
tm <- delete.response(terms(lmObject))
## linear predictor matrix
Xp <- model.matrix(tm, newdata)
## predicted values by direct matrix-vector multiplication
pred <- c(Xp %*% coef(lmObject))
## mean of the aggregation
agg_mean <- c(crossprod(pred, w))
## residual variance
sig2 <- c(crossprod(residuals(lmObject))) / df.residual(lmObject)
## efficiently compute variance of the aggregation without matrix-matrix computations
QR <- lmObject$qr ## qr object of fitted model
piv <- QR$pivot ## pivoting index
r <- QR$rank ## model rank / numeric rank
u <- forwardsolve(t(QR$qr), c(crossprod(Xp, w))[piv], r)
agg_variance <- c(crossprod(u)) * sig2
## adjusted variance of the aggregation
agg_variance_adj <- agg_variance + c(crossprod(w)) * sig2
## t-distribution quantiles
Qt <- c(-1, 1) * qt((1 - alpha) / 2, lmObject$df.residual, lower.tail = FALSE)
## names of CI and PI
NAME <- c("lower", "upper")
## CI
CI <- setNames(agg_mean + Qt * sqrt(agg_variance), NAME)
## PI
PI <- setNames(agg_mean + Qt * sqrt(agg_variance_adj), NAME)
## return
list(mean = agg_mean, var = agg_variance, CI = CI, PI = PI)
}
Давайте проведем быстрый тест.
## sum opeartion
fast_agg_pred(rep(1, nrow(newdat)), lm.tree, newdat)
#$mean
#[1] 111.512
#
#$var
#[1] 6.671575
#
#$CI
# lower upper
#106.2210 116.8029
#
#$PI
# lower upper
# 96.86122 126.16268
## average operation
fast_agg_pred(rep(1, nrow(newdat)) / nrow(newdat), lm.tree, newdat)
#$mean
#[1] 27.87799
#
#$var
#[1] 0.4169734
#
#$CI
# lower upper
#26.55526 29.20072
#
#$PI
# lower upper
#24.21531 31.54067
Да, ответ правильный!