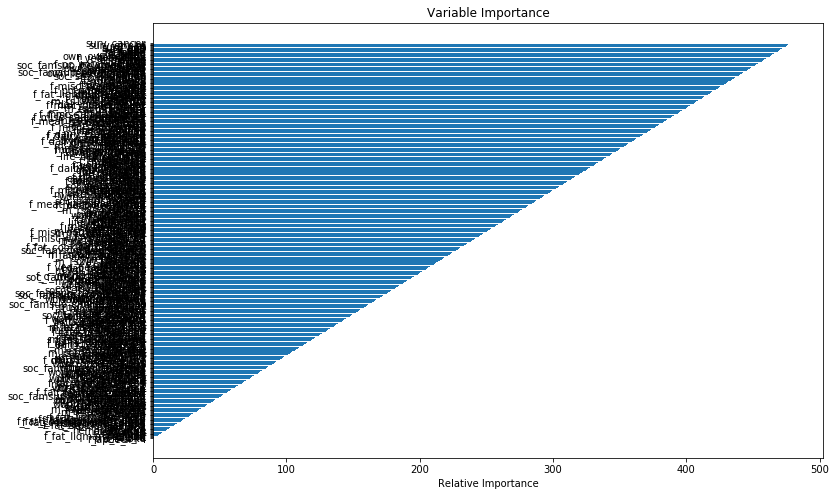
Значение невероятной переменной для выживания GBM: постоянная разница в важности
У меня есть вопрос об анализе выживания GBM. Я пытаюсь количественно оценить значение переменных для моих переменных (n=453) в наборе данных из 3614 человек. Результирующий график с переменными значениями выглядит подозрительно упорядоченным. Я раньше вычислял GBM, но никогда не видел важность этого постепенного паттерна. Между барами важности обычно существуют разные расстояния; в этом случае кажется, что есть постоянная разница в важности. Мой фрейм данных называется df. Я не могу загрузить образцы данных из-за чувствительности данных. Вместо этого мой вопрос касается вероятности получения этих переменных значений.
from sksurv.ensemble import GradientBoostingSurvivalAnalysis
from sklearn import crossvalidation, metrics, model_selection
from sklearn.grid_search import GridSearchCV
import matplotlib.pylab as plt
%matplotlib inline
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 12, 4
from sklearn.datasets import make_regression
predictors = [x for x in df.columns if x not in 'death','surv_death']]
target = ['death','surv_death']
df_X=df[predictors]
df_y=df[target]
X=df_X.values
arr_y=df_y.values
y= np.zeros((n,), dtype=[('death','bool'),('surv_death', 'f8')])
y['death']=arr_y[:,1].flatten()
y['surv_death']=arr_y[:,1].flatten()
gbm0 = GradientBoostingSurvivalAnalysis(criterion='friedman_mse',
dropout_rate=0 .0, learning_rate=0.01, loss='coxph', max_depth=100,
max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=10, min_samples_split=20,
min_weight_fraction_leaf=0.0, n_estimators=1000, random_state=10,
subsample=1.0, verbose=0) dropout_rate=0.0,
learning_rate=0.01, loss='coxph', max_depth=100,
max_features=None, max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=10, min_samples_split=20,
min_weight_fraction_leaf=0.0, n_estimators=1000, random_state=10,
subsample=1.0, verbose=0)
gbm0.fit(X, y)
feature_importance = gbm0.feature_importances_
feature_importance = 100.0 * (feature_importance /feature_importance.max())
sorted_idx = np.argsort(feature_importance)
preds=np.array(predictors)[sorted_idx]
pos = np.arange(sorted_idx.shape[0]) + .5
plt.figure(figsize=(10, 100))
plt.subplot(1, 1, 1)
plt.barh(preds,pos,align='center')
plt.xlabel('Relative Importance')
plt.title('Variable Importance')
plt.savefig("df.png")
plt.show()